2018年高中数学第一章常用逻辑用语1.2.1“且”与“或”课件2新人教B版选修2_1(27张)
文档属性
| 名称 | 2018年高中数学第一章常用逻辑用语1.2.1“且”与“或”课件2新人教B版选修2_1(27张) |  | |
| 格式 | zip | ||
| 文件大小 | 584.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 22:40:53 | ||
图片预览






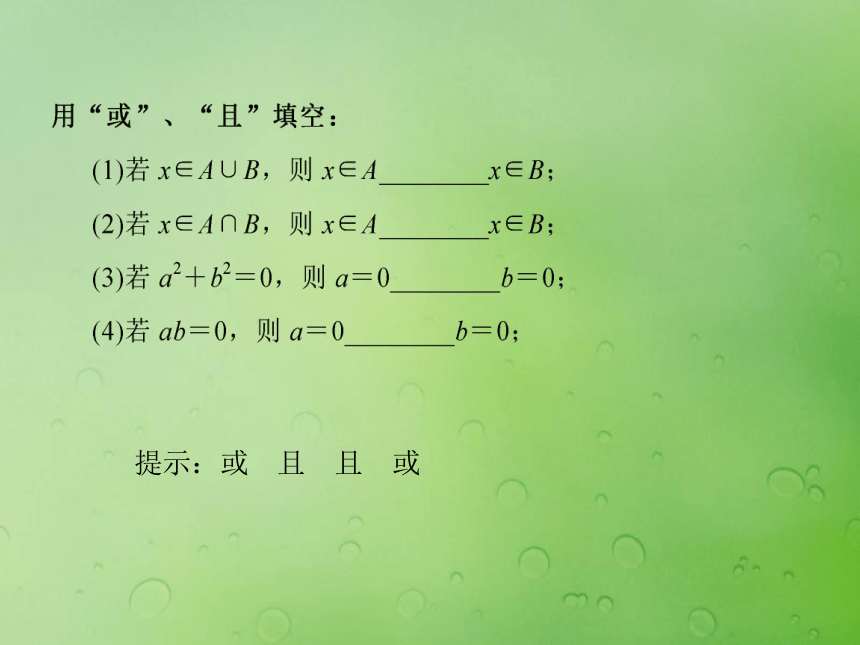
文档简介
课件27张PPT。1.2.1 “且”与“或” 有一天,水中生物村要庆祝鲤鱼爷爷的六十大寿。鱼儿们宣布:“请所有水中生物来参加鲤鱼爷爷的寿宴!有丰盛的餐点唷!”听到这个消息的陆地动物,都感到浑身不是滋味。住在池塘边的青蛙跳进水里,尝尽寿宴桌上的山珍海味。过了几天,陆地上的熊叔叔家办儿子满月餐会。陆地动物宣布:“请所有陆地动物来参加熊叔叔儿子的满月酒席!有丰盛的餐点和礼物喔!”水中生物气得七窍生烟。青蛙仍然酒足饭饱。为了友好,陆地动物和水中生物决定共同举行隆重的酒会。宣布消息:“生活在水中或陆地上的动物,可以来参加庆祝会。”青蛙又来了,水、陆生物对青蛙都很生气。决定重新宣布:“除了‘生活在水中并且生活在陆地上’的动物之外,所有的动物都来参加庆祝会!”,现在可怜的青蛙不能参加庆祝会了!课题引入逻辑联结词“且”下列三个命题间有什么关系?
(1)12能被3整除;
(2)12能被4整除;
(3)12能被3整除且能被4整除。可发现,命题(3)是由命题(1)(2)使用联结词“且”
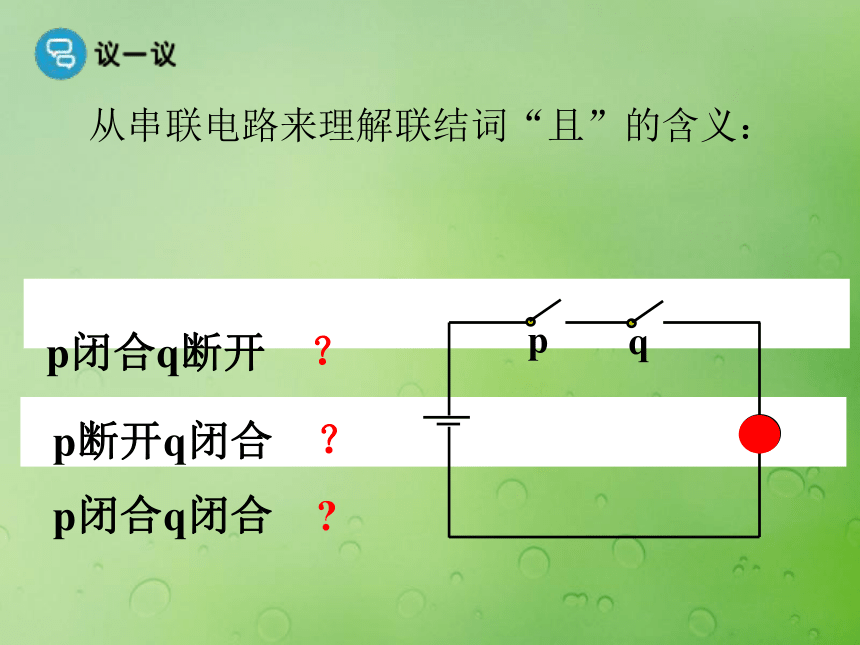
联结得到的新命题。探究问题—1一般地,使用联结词“且” 把命题p和命题q联结起来就得到一个新命题。记作: p?q读作: p且q从串联电路来理解联结词“且”的含义:pqp闭合q断开 ?p断开q闭合 ? p闭合q闭合 ?逻辑联结词“或”下列三个命题间有什么关系?
27是7的倍数;
27是9的倍数;
27是7的倍数或是9的倍数。可发现,命题(3)是由命题(1)(2)使用联结词“或”
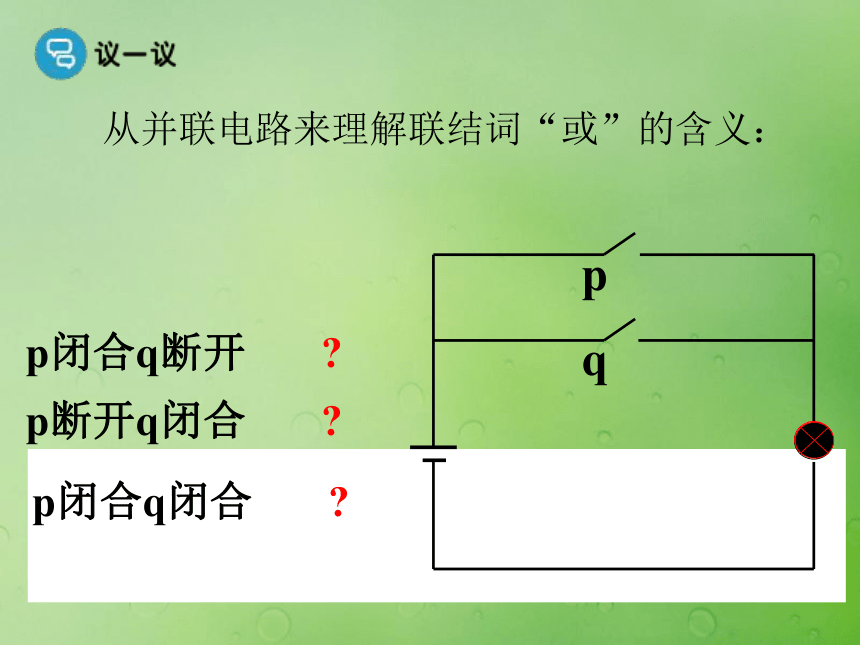
联结得到的新命题。探究问题二2一般地,使用联结词“或” 把命题p和命题q联结起来就得到一个新命题。记作: p?q读作: p或q从并联电路来理解联结词“或”的含义:pqp闭合q断开 ?p断开q闭合 ?p闭合q闭合 ?提示:或 且 且 或探究问题三1 真假假假真值表p∧q形式:全真才真,一假则假。
2真值表真假真真p∨q形式:一真则真,全假才假.如果p?q为真命题,
那么p?q一定是真命题吗?一定如果p?q 为真命题,
那么p?q一定是真命题吗?不一定例1 把下列各组命题用“且”联结组成新命题,并判断其真假.(1)(2)解(1)(2)典例分析例2 把下列各组命题用“或”联结成新命题,并判断它们的真假.1.将下列命题用“且”联结成新命题,并判断它们的真假;
(1)p:菱形的对角线相等,
q:菱形的对角线互相平分
(2) p:35是5的倍数,
q:35是7的倍数。解:(1) p?q:菱形的对角线相等且互相平分。由于p假、q真,从而p?q假。由于p真、q真,从而p?q真。(2) p?q: 35是5的倍数且35是7的倍数。快问快答 (3)p: 5是10的约数,q:5是15的约数
p且q: 5是10的约数且是15的约数
(4)p: 矩形的对角线相等,q:矩形的对角线互相垂直
p且q:矩形对角线相等且互相垂直
(5)p:π是有理数,q:π是自然数
p且q:π是有理数且是自然数
真假假2.将下列命题用“或”联结成新命题,并判断它们的真假(2) p:9是奇数,q:9是质数;真真真真(1) p:12是3的倍数,q:12是8的倍数
p或q:12是3的倍数或是8的倍数
(4) P:N?Z. q:{0}?N;
p或q:9是奇数或是质数
(3) p:一次函数是单调函数,q:一次函数是奇函数
p或q:一次函数是单调函数或是奇函数 p或q:N?Z或{0}?N.
1.下面命题使用了什么逻辑联结词?并判断真假。9?19。
(2) x=?1是方程x2-1=0的解。
(3) A?B ?R (其中A={1,2},B={1,2,3})
(4)等腰三角形顶角的平分线平分底边并且垂直于底边;
(5)属于集合Q也属于集合R.或或且假真真且真且真课堂检测1.“且”:当p,q都是真命题时,p?q是真命题; 当p,q两个命题中有一个命题是假命题时,
p?q是假命题;口诀:全真才真,一假则假.当p,q都是假命题时,p ? q是假命题; 2.“或”:当p,q两个命题中有一个命题是真命题时,
p ? q是真命题;口诀:一真则真,全假才假.
课堂小结作业布置教材P13练习A,P14练习B课后拓展利用逻辑连接词的真假求参数取值范围谢谢大家!
(1)12能被3整除;
(2)12能被4整除;
(3)12能被3整除且能被4整除。可发现,命题(3)是由命题(1)(2)使用联结词“且”
联结得到的新命题。探究问题—1一般地,使用联结词“且” 把命题p和命题q联结起来就得到一个新命题。记作: p?q读作: p且q从串联电路来理解联结词“且”的含义:pqp闭合q断开 ?p断开q闭合 ? p闭合q闭合 ?逻辑联结词“或”下列三个命题间有什么关系?
27是7的倍数;
27是9的倍数;
27是7的倍数或是9的倍数。可发现,命题(3)是由命题(1)(2)使用联结词“或”
联结得到的新命题。探究问题二2一般地,使用联结词“或” 把命题p和命题q联结起来就得到一个新命题。记作: p?q读作: p或q从并联电路来理解联结词“或”的含义:pqp闭合q断开 ?p断开q闭合 ?p闭合q闭合 ?提示:或 且 且 或探究问题三1 真假假假真值表p∧q形式:全真才真,一假则假。
2真值表真假真真p∨q形式:一真则真,全假才假.如果p?q为真命题,
那么p?q一定是真命题吗?一定如果p?q 为真命题,
那么p?q一定是真命题吗?不一定例1 把下列各组命题用“且”联结组成新命题,并判断其真假.(1)(2)解(1)(2)典例分析例2 把下列各组命题用“或”联结成新命题,并判断它们的真假.1.将下列命题用“且”联结成新命题,并判断它们的真假;
(1)p:菱形的对角线相等,
q:菱形的对角线互相平分
(2) p:35是5的倍数,
q:35是7的倍数。解:(1) p?q:菱形的对角线相等且互相平分。由于p假、q真,从而p?q假。由于p真、q真,从而p?q真。(2) p?q: 35是5的倍数且35是7的倍数。快问快答 (3)p: 5是10的约数,q:5是15的约数
p且q: 5是10的约数且是15的约数
(4)p: 矩形的对角线相等,q:矩形的对角线互相垂直
p且q:矩形对角线相等且互相垂直
(5)p:π是有理数,q:π是自然数
p且q:π是有理数且是自然数
真假假2.将下列命题用“或”联结成新命题,并判断它们的真假(2) p:9是奇数,q:9是质数;真真真真(1) p:12是3的倍数,q:12是8的倍数
p或q:12是3的倍数或是8的倍数
(4) P:N?Z. q:{0}?N;
p或q:9是奇数或是质数
(3) p:一次函数是单调函数,q:一次函数是奇函数
p或q:一次函数是单调函数或是奇函数 p或q:N?Z或{0}?N.
1.下面命题使用了什么逻辑联结词?并判断真假。9?19。
(2) x=?1是方程x2-1=0的解。
(3) A?B ?R (其中A={1,2},B={1,2,3})
(4)等腰三角形顶角的平分线平分底边并且垂直于底边;
(5)属于集合Q也属于集合R.或或且假真真且真且真课堂检测1.“且”:当p,q都是真命题时,p?q是真命题; 当p,q两个命题中有一个命题是假命题时,
p?q是假命题;口诀:全真才真,一假则假.当p,q都是假命题时,p ? q是假命题; 2.“或”:当p,q两个命题中有一个命题是真命题时,
p ? q是真命题;口诀:一真则真,全假才假.
课堂小结作业布置教材P13练习A,P14练习B课后拓展利用逻辑连接词的真假求参数取值范围谢谢大家!
