2018年高中数学第一章常用逻辑用语1.3.2命题的四种形式课件2新人教B版选修2_1(18张)
文档属性
| 名称 | 2018年高中数学第一章常用逻辑用语1.3.2命题的四种形式课件2新人教B版选修2_1(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 488.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 22:42:14 | ||
图片预览





文档简介
课件18张PPT。1.3.2命题的四种形式知识回顾把下列命题改写成“若p,则q”的形式,并
写出它们的逆命题。
1、正方形的四条边相等;
2、两条平行直线不相交;
3、菱形的对角线互相垂直平分。解:1、原命题:若一个四边形是正方形,则它的四条边相等。逆命题:若一个四边形的四条边相等,则它是正方形。2、原命题:若两条直线平行,则这两条直线不相交。逆命题:若两条直线不相交,则这两条直线平行。3、原命题:若一个四边形是菱形,则它的对角线互相
垂直平分。逆命题:若一个四边形的对角线互相垂直平分,则
它是菱形。引例命题1:若同位角相等,则两直线平行;命题2:若两直线平行,则同位角相等;命题3:若同位角不相等,则两直线不平行;命题4:若两直线不平行,则同位角不相等。问:命题1与命题2、3、4的条件与结
论有什么关系? 变式训练:原命题:若同位角不相等,则两直线不平行逆命题:否命题:逆否命题:若两直线不平行,则同位角不相等若同位角相等,则两直线平行若两直线平行,则同位角相等例1:写出下列命题的逆命题、否命题、逆否命题并判断其
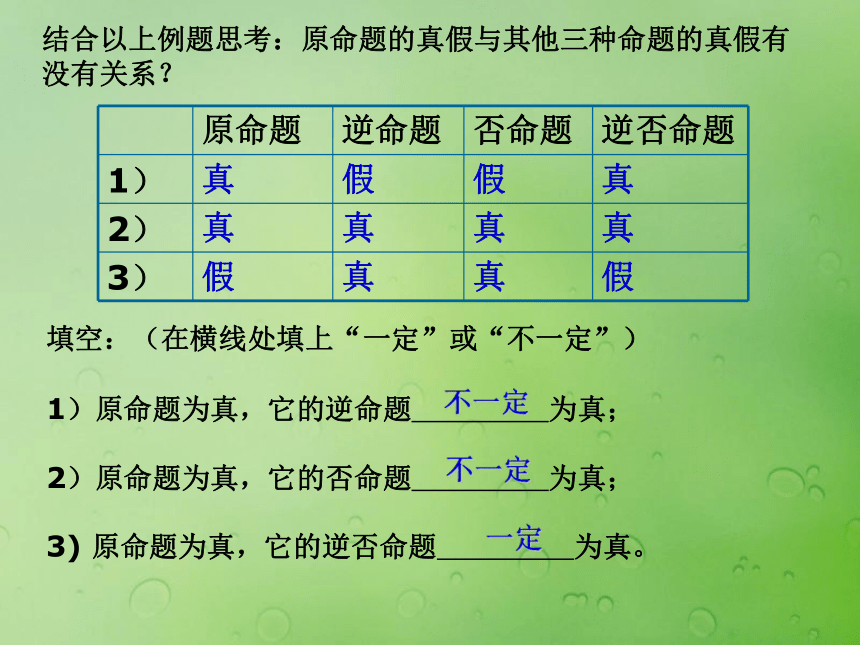
真假。1、若x=0且y=0,则xy=0。3、若a+b是偶数,则a和b都是偶数。2、若a-b>0,则a>b。逆命题:若a和b都是偶数,则a+b是偶数否命题:若a+b不是偶数,则a和b不都是偶数逆否命题:若a和b不都是偶数,则a+b不是偶数假假真真结合以上例题思考:原命题的真假与其他三种命题的真假有
没有关系?填空:(在横线处填上“一定”或“不一定”)
1)原命题为真,它的逆命题 为真;
2)原命题为真,它的否命题 为真;
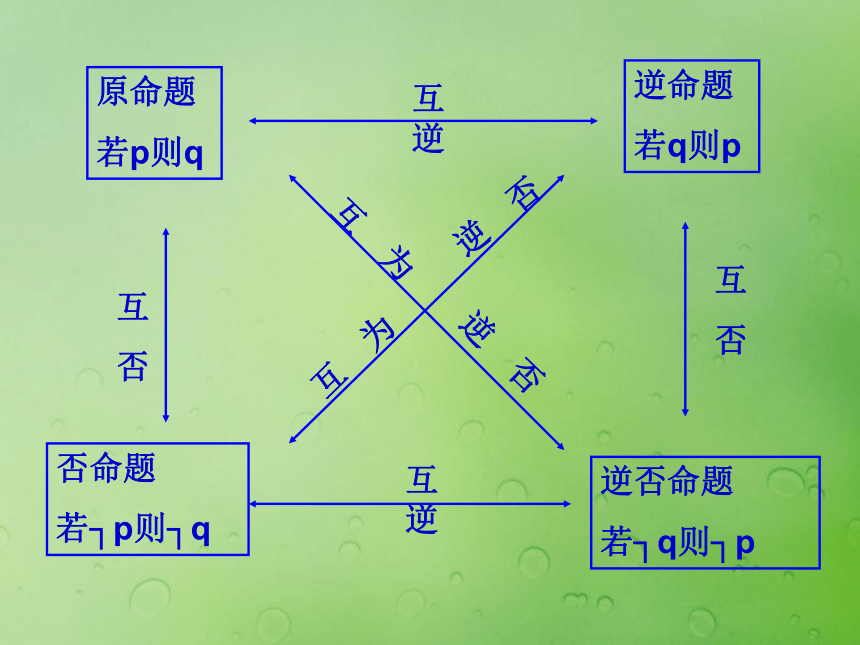
3) 原命题为真,它的逆否命题 为真。不一定不一定一定原命题
若p则q否命题
若┐p则┐q逆否命题
若┐q则┐p逆命题
若q则p互
否互 逆互 逆互
否互 为互 为逆 否逆 否结 论:原命题与逆否命题同真假。原命题的逆命题与否命题同真假。(2)两个命题为互逆命题或互否命题,它们的真假性
没有关系。(1)p?q??q??p四种命题的真假之间的关系如下:例2 写出下列命题的逆命题、否命题、逆否命题,并
判断这些命题的真假。 1、当 c>0时,若a>b,则ac>bc。2、若x=y,则 真逆命题:当 c>0时,若ac>bc ,则 a>b。
真否命题:当 c>0时,若a≤b,则ac≤bc。
真逆否命题:当 c>0时,若ac≤bc ,则 a≤b。
真逆命题:若 ,则x=y。否命题:若x≠y,则 。 逆否命题:若 ,则x≠y。真真假假例3与命题“若 ,则 ”等价的
命题是 ( )
A、若 ,则
B、若 ,则
C、若 ,则
D、若 ,则D巩固练习:判断命题的真假2)若 ,则实数a和b不都小于1。逆否命题:若x=1且y=2 ,则x+y=3。 逆否命题:若实数a和b都小于1 ,则 真真真真1、若x+y≠3,则x≠1或y≠2。命题的否定与否命题 的区别:1、概念:命题的否定: 对命题的 进行否定;
否命题:对原命题的 和 分别否定后组成的命题。 2、结构:对于“若p,则q”形式的命题,其命题的否定为
“若 ,则 ”,也就是不改变条件,而否定结论;
而否命题则为“若 ,则 ”。 3、真值:命题的否定的真值与原命题 ;
而否命题的真值与原命题 。 结论条件结论p非q非q非p相反无关例4、写出下列命题的否定形式及否命题。1、全等三角形的面积相等。命题的否定:全等三角形的面积不相等。否命题:不全等的三角形面积不相等。2、若 ,则实数m、n、a、b全为零。 否命题:若 ,则实数m、n、
a、b不全为零。
3、若xy=0,则x=0或y=0 否命题:若xy≠0,则x≠0且y≠0。 命题的否定:若xy=0,则x≠0且y≠0。 练习: 1、写出下列命题的否定形式和否命题
(1)若abc=0,则a、b、c中至少有一个为零。(2)若命题的否定:若abc=0,则a、b、c全不为零。否命题: 若abc≠0,则a、b、c全不为零。
命题的否定:若否命题: 若2、 命题“ 使得 ”的否定为( )A、B、C、D、c3、已知命题甲:“若p,则q”;命题乙:“若q,则p”;
命题丙:“若 ,则 ”;命题丁:“若 ,则 ”。
则下列命题正确的是( )
(1)若甲真则乙为真 (2)若乙真则丙为真
(3)若丙真则丁为真 (4)若丁真则甲为真
A、(1)(2) B、 (3)(4)
C、 (2)(3 ) D、 (2)(4) D4、判断命题“已知a、x为实数,若关于x的不等式
的解集非空,则 ”
的逆否命题的真假.分析:根据等价性,可直接判断原命题的真假。解:因为原不等式的解集非空,
所以 即
解得 ,所以原命题为真,
又因为原命题与其逆否命题等价,所以其逆否命题为真。 小结1、命题的四种形式;2、四种形式间的真假关系;3、四种形式间的等价关系;4、命题的否定与否命题的区别。
写出它们的逆命题。
1、正方形的四条边相等;
2、两条平行直线不相交;
3、菱形的对角线互相垂直平分。解:1、原命题:若一个四边形是正方形,则它的四条边相等。逆命题:若一个四边形的四条边相等,则它是正方形。2、原命题:若两条直线平行,则这两条直线不相交。逆命题:若两条直线不相交,则这两条直线平行。3、原命题:若一个四边形是菱形,则它的对角线互相
垂直平分。逆命题:若一个四边形的对角线互相垂直平分,则
它是菱形。引例命题1:若同位角相等,则两直线平行;命题2:若两直线平行,则同位角相等;命题3:若同位角不相等,则两直线不平行;命题4:若两直线不平行,则同位角不相等。问:命题1与命题2、3、4的条件与结
论有什么关系? 变式训练:原命题:若同位角不相等,则两直线不平行逆命题:否命题:逆否命题:若两直线不平行,则同位角不相等若同位角相等,则两直线平行若两直线平行,则同位角相等例1:写出下列命题的逆命题、否命题、逆否命题并判断其
真假。1、若x=0且y=0,则xy=0。3、若a+b是偶数,则a和b都是偶数。2、若a-b>0,则a>b。逆命题:若a和b都是偶数,则a+b是偶数否命题:若a+b不是偶数,则a和b不都是偶数逆否命题:若a和b不都是偶数,则a+b不是偶数假假真真结合以上例题思考:原命题的真假与其他三种命题的真假有
没有关系?填空:(在横线处填上“一定”或“不一定”)
1)原命题为真,它的逆命题 为真;
2)原命题为真,它的否命题 为真;
3) 原命题为真,它的逆否命题 为真。不一定不一定一定原命题
若p则q否命题
若┐p则┐q逆否命题
若┐q则┐p逆命题
若q则p互
否互 逆互 逆互
否互 为互 为逆 否逆 否结 论:原命题与逆否命题同真假。原命题的逆命题与否命题同真假。(2)两个命题为互逆命题或互否命题,它们的真假性
没有关系。(1)p?q??q??p四种命题的真假之间的关系如下:例2 写出下列命题的逆命题、否命题、逆否命题,并
判断这些命题的真假。 1、当 c>0时,若a>b,则ac>bc。2、若x=y,则 真逆命题:当 c>0时,若ac>bc ,则 a>b。
真否命题:当 c>0时,若a≤b,则ac≤bc。
真逆否命题:当 c>0时,若ac≤bc ,则 a≤b。
真逆命题:若 ,则x=y。否命题:若x≠y,则 。 逆否命题:若 ,则x≠y。真真假假例3与命题“若 ,则 ”等价的
命题是 ( )
A、若 ,则
B、若 ,则
C、若 ,则
D、若 ,则D巩固练习:判断命题的真假2)若 ,则实数a和b不都小于1。逆否命题:若x=1且y=2 ,则x+y=3。 逆否命题:若实数a和b都小于1 ,则 真真真真1、若x+y≠3,则x≠1或y≠2。命题的否定与否命题 的区别:1、概念:命题的否定: 对命题的 进行否定;
否命题:对原命题的 和 分别否定后组成的命题。 2、结构:对于“若p,则q”形式的命题,其命题的否定为
“若 ,则 ”,也就是不改变条件,而否定结论;
而否命题则为“若 ,则 ”。 3、真值:命题的否定的真值与原命题 ;
而否命题的真值与原命题 。 结论条件结论p非q非q非p相反无关例4、写出下列命题的否定形式及否命题。1、全等三角形的面积相等。命题的否定:全等三角形的面积不相等。否命题:不全等的三角形面积不相等。2、若 ,则实数m、n、a、b全为零。 否命题:若 ,则实数m、n、
a、b不全为零。
3、若xy=0,则x=0或y=0 否命题:若xy≠0,则x≠0且y≠0。 命题的否定:若xy=0,则x≠0且y≠0。 练习: 1、写出下列命题的否定形式和否命题
(1)若abc=0,则a、b、c中至少有一个为零。(2)若命题的否定:若abc=0,则a、b、c全不为零。否命题: 若abc≠0,则a、b、c全不为零。
命题的否定:若否命题: 若2、 命题“ 使得 ”的否定为( )A、B、C、D、c3、已知命题甲:“若p,则q”;命题乙:“若q,则p”;
命题丙:“若 ,则 ”;命题丁:“若 ,则 ”。
则下列命题正确的是( )
(1)若甲真则乙为真 (2)若乙真则丙为真
(3)若丙真则丁为真 (4)若丁真则甲为真
A、(1)(2) B、 (3)(4)
C、 (2)(3 ) D、 (2)(4) D4、判断命题“已知a、x为实数,若关于x的不等式
的解集非空,则 ”
的逆否命题的真假.分析:根据等价性,可直接判断原命题的真假。解:因为原不等式的解集非空,
所以 即
解得 ,所以原命题为真,
又因为原命题与其逆否命题等价,所以其逆否命题为真。 小结1、命题的四种形式;2、四种形式间的真假关系;3、四种形式间的等价关系;4、命题的否定与否命题的区别。
