高一数学人教版(必修2) 平面与直线的位置关系 练习含解析
文档属性
| 名称 | 高一数学人教版(必修2) 平面与直线的位置关系 练习含解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 454.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-25 00:00:00 | ||
图片预览


文档简介
高考资源网( www.ks5u.com),您身边的高考专家
高考资源网( www.ks5u.com),您身边的高考专家
11月18日 每周一测
高考频度:★★★★★ 难易程度:★★★☆☆
学霸推荐
1.如图所示,长方体ABCD-A1B1C1D1中,E、F分别是棱AA1和BB1的中点,过EF的平面EFGH分别交BC和AD于G、H,则HG和AB的位置关系是
A.平行 B.相交
C.异面 D.平行或异面
2.过平面α外的直线l作一组平面与α相交,如果所得的交线为a,b,c,…,则这些交线的位置关系为
A.都平行 B.都相交且一定交于同一点
C.都相交但不一定交于同一点 D.都平行或交于同一点
3.如图所示,P是三角形ABC所在平面外一点,平面α∥平面ABC,α分别交线段PA,PB,PC于A′,B′,C′,若PA′∶AA′=2∶3,则S△A′B′C′∶S△ABC=
A.2∶25 B.4∶25
C.2∶5 D.4∶5
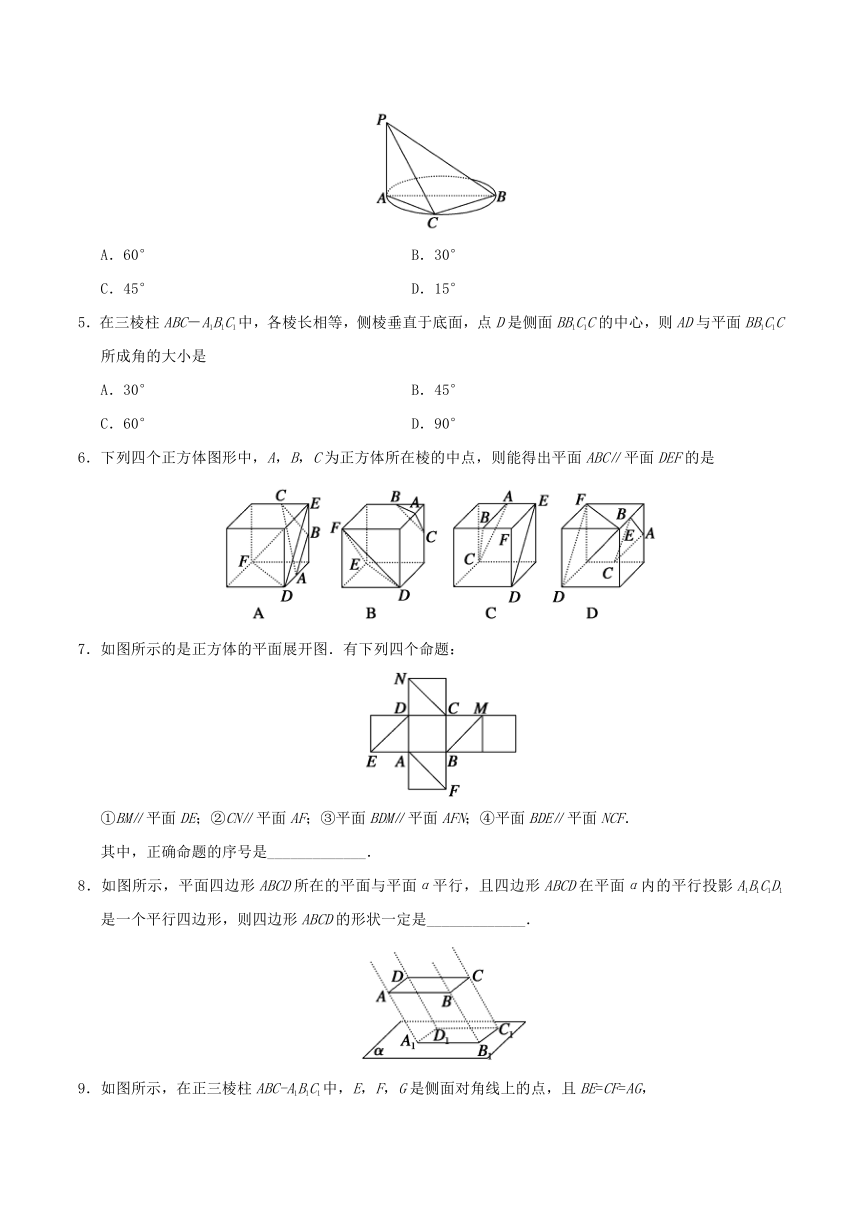
4.如图,AB是圆的直径,PA垂直于圆所在的平面,C是圆上一点(不同于A、B)且PA=AC,则二面角P-BC-A的大小为
A.60° B.30°
C.45° D.15°
5.在三棱柱ABC-A1B1C1中,各棱长相等,侧棱垂直于底面,点D是侧面BB1C1C的中心,则AD与平面BB1C1C所成角的大小是
A.30° B.45°
C.60° D.90°
6.下列四个正方体图形中,A,B,C为正方体所在棱的中点,则能得出平面ABC∥平面DEF的是
7.如图所示的是正方体的平面展开图.有下列四个命题:
①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.
其中,正确命题的序号是_____________.
8.如图所示,平面四边形ABCD所在的平面与平面α平行,且四边形ABCD在平面α内的平行投影A1B1C1D1是一个平行四边形,则四边形ABCD的形状一定是_____________.
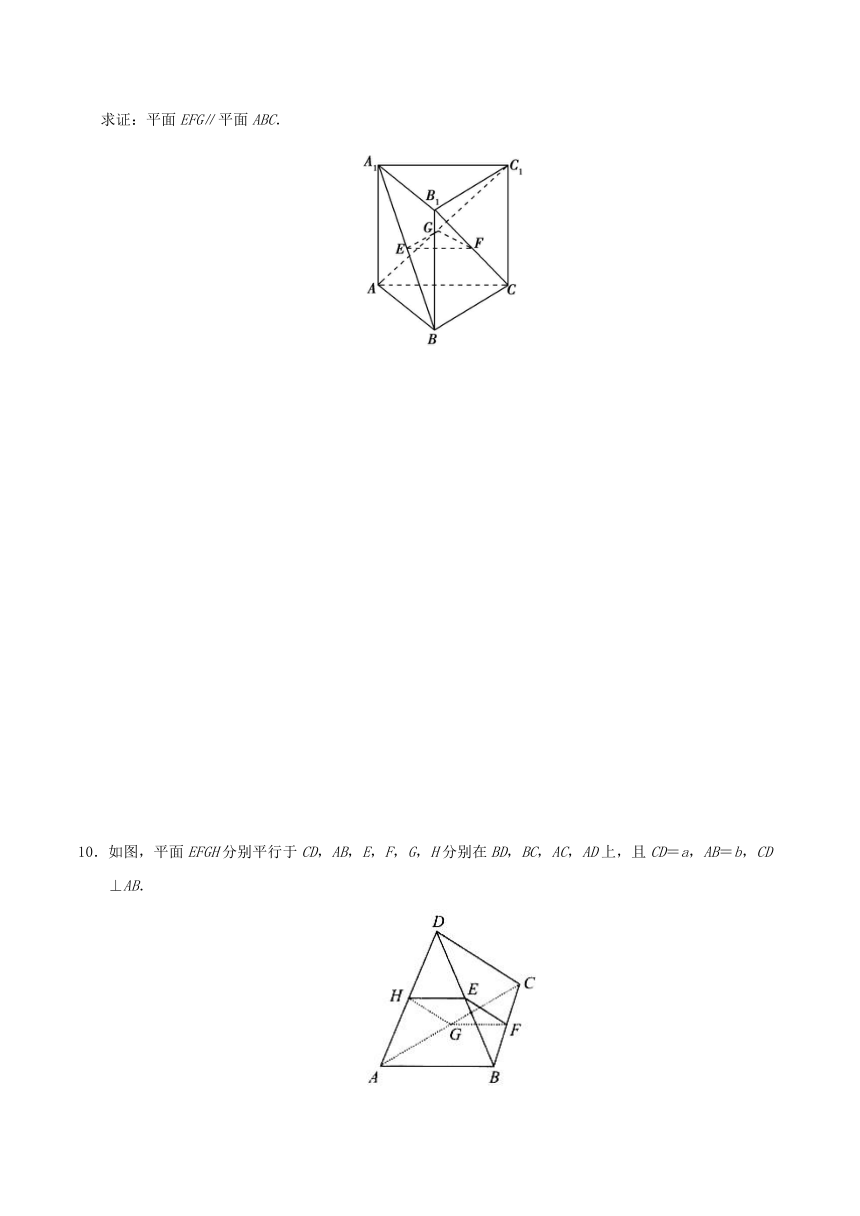
9.如图所示,在正三棱柱ABC-A1B1C1中,E,F,G是侧面对角线上的点,且BE=CF=AG,
求证:平面EFG∥平面ABC.
10.如图,平面EFGH分别平行于CD,AB,E,F,G,H分别在BD,BC,AC,AD上,且CD=a,AB=b,CD⊥AB.
(1)求证:EFGH是矩形.
(2)设DE=m,EB=n,求矩形EFGH的面积.
11.如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ与平面PAO平行?
12.如图,过点引三条不共面的直线其中,且.求证:平面⊥平面.
2.【答案】D
【解析】若l∥α,则l∥a,l∥b,l∥c,…,所以a∥b∥c∥…;若l∩α=P,则a,b,c,…交于点P.
3.【答案】B
【解析】由题意知A′B′∥AB,B′C′∥BC,C′A′∥CA,且PA′∶AA′=2∶3,∴===.∴S△A′B′C′∶S△ABC=4∶25.
4.【答案】C
【解析】易得BC⊥平面PAC,所以∠PCA是二面角P-BC-A的平面角,在Rt△PAC中,PA=AC,所以∠PCA=45°.故选C.
5.【答案】C
【解析】取BC的中点E,连接AE,ED,AD,则AE⊥平面BB1C1C,故∠ADE为直线AD与平面BB1C1C所成的角.设各棱长为a,则AE=a,DE=.∴tan∠ADE=.∴∠ADE=60°.
6.【答案】B
【解析】B中,可证AB∥DE,BC∥DF,故可以证明AB∥平面DEF,BC∥平面DEF.又AB∩BC=B,所以平面ABC∥平面DEF.故选B.
7.【答案】①②③④
【解析】展开图可以折成如图(1)所示的正方体.
8.【答案】平行四边形
【解析】由面面平行的性质定理可以推出四边形ABCD的两组对边分别平行,故四边形ABCD是平行四边形.
9.【答案】证明详见解析.
【解析】过点E作EP⊥BB1于P,连接PF.
在正三棱柱ABC-A1B1C1的侧面ABB1A1中,易知A1B1⊥BB1,
∵EP⊥BB1,∴EP∥A1B1∥AB,
∴,EP∥平面ABC.
又BE=CF,BA1=CB1,∴,
∴PF∥BC,则PF∥平面ABC.
又EP∩PF=P,
∴平面PEF∥平面ABC.
∵EF?平面PEF,∴EF∥平面ABC.
同理,GF∥平面ABC.
又EF∩GF=F,∴平面EFG∥平面ABC.
10.【答案】(1)证明详见解析;(2).
(2)由(1)可知在中,EF∥CD,DE=m,EB=n,
所以.
又CD=a,所以.
由HE∥AB,得.
又因为AB=b,所以.
又因为四边形EFGH为矩形,
所以.
11.【答案】当Q为CC1的中点时,平面D1BQ∥平面PAO.
【解析】Q为CC1的中点.证明如下:
如图,设平面D1BQ∩平面ADD1A1=D1M,点M在AA1上,
由于平面D1BQ∩平面BCC1B1=BQ,平面ADD1A1∥平面BCC1B1,
由面面平行的性质定理可得BQ∥D1M.
12.【答案】证明详见解析.
【解析】∵,
∴和都是等边三角形,
∴.
如图,取的中点,连接,∴.
在中,,
∴,
∴.
在中,, ,
欢迎广大教师踊跃来稿,稿酬丰厚。 www.ks5u.com
欢迎广大教师踊跃来稿,稿酬丰厚。 www.ks5u.com
高考资源网( www.ks5u.com),您身边的高考专家
11月18日 每周一测
高考频度:★★★★★ 难易程度:★★★☆☆
学霸推荐
1.如图所示,长方体ABCD-A1B1C1D1中,E、F分别是棱AA1和BB1的中点,过EF的平面EFGH分别交BC和AD于G、H,则HG和AB的位置关系是
A.平行 B.相交
C.异面 D.平行或异面
2.过平面α外的直线l作一组平面与α相交,如果所得的交线为a,b,c,…,则这些交线的位置关系为
A.都平行 B.都相交且一定交于同一点
C.都相交但不一定交于同一点 D.都平行或交于同一点
3.如图所示,P是三角形ABC所在平面外一点,平面α∥平面ABC,α分别交线段PA,PB,PC于A′,B′,C′,若PA′∶AA′=2∶3,则S△A′B′C′∶S△ABC=
A.2∶25 B.4∶25
C.2∶5 D.4∶5
4.如图,AB是圆的直径,PA垂直于圆所在的平面,C是圆上一点(不同于A、B)且PA=AC,则二面角P-BC-A的大小为
A.60° B.30°
C.45° D.15°
5.在三棱柱ABC-A1B1C1中,各棱长相等,侧棱垂直于底面,点D是侧面BB1C1C的中心,则AD与平面BB1C1C所成角的大小是
A.30° B.45°
C.60° D.90°
6.下列四个正方体图形中,A,B,C为正方体所在棱的中点,则能得出平面ABC∥平面DEF的是
7.如图所示的是正方体的平面展开图.有下列四个命题:
①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.
其中,正确命题的序号是_____________.
8.如图所示,平面四边形ABCD所在的平面与平面α平行,且四边形ABCD在平面α内的平行投影A1B1C1D1是一个平行四边形,则四边形ABCD的形状一定是_____________.
9.如图所示,在正三棱柱ABC-A1B1C1中,E,F,G是侧面对角线上的点,且BE=CF=AG,
求证:平面EFG∥平面ABC.
10.如图,平面EFGH分别平行于CD,AB,E,F,G,H分别在BD,BC,AC,AD上,且CD=a,AB=b,CD⊥AB.
(1)求证:EFGH是矩形.
(2)设DE=m,EB=n,求矩形EFGH的面积.
11.如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ与平面PAO平行?
12.如图,过点引三条不共面的直线其中,且.求证:平面⊥平面.
2.【答案】D
【解析】若l∥α,则l∥a,l∥b,l∥c,…,所以a∥b∥c∥…;若l∩α=P,则a,b,c,…交于点P.
3.【答案】B
【解析】由题意知A′B′∥AB,B′C′∥BC,C′A′∥CA,且PA′∶AA′=2∶3,∴===.∴S△A′B′C′∶S△ABC=4∶25.
4.【答案】C
【解析】易得BC⊥平面PAC,所以∠PCA是二面角P-BC-A的平面角,在Rt△PAC中,PA=AC,所以∠PCA=45°.故选C.
5.【答案】C
【解析】取BC的中点E,连接AE,ED,AD,则AE⊥平面BB1C1C,故∠ADE为直线AD与平面BB1C1C所成的角.设各棱长为a,则AE=a,DE=.∴tan∠ADE=.∴∠ADE=60°.
6.【答案】B
【解析】B中,可证AB∥DE,BC∥DF,故可以证明AB∥平面DEF,BC∥平面DEF.又AB∩BC=B,所以平面ABC∥平面DEF.故选B.
7.【答案】①②③④
【解析】展开图可以折成如图(1)所示的正方体.
8.【答案】平行四边形
【解析】由面面平行的性质定理可以推出四边形ABCD的两组对边分别平行,故四边形ABCD是平行四边形.
9.【答案】证明详见解析.
【解析】过点E作EP⊥BB1于P,连接PF.
在正三棱柱ABC-A1B1C1的侧面ABB1A1中,易知A1B1⊥BB1,
∵EP⊥BB1,∴EP∥A1B1∥AB,
∴,EP∥平面ABC.
又BE=CF,BA1=CB1,∴,
∴PF∥BC,则PF∥平面ABC.
又EP∩PF=P,
∴平面PEF∥平面ABC.
∵EF?平面PEF,∴EF∥平面ABC.
同理,GF∥平面ABC.
又EF∩GF=F,∴平面EFG∥平面ABC.
10.【答案】(1)证明详见解析;(2).
(2)由(1)可知在中,EF∥CD,DE=m,EB=n,
所以.
又CD=a,所以.
由HE∥AB,得.
又因为AB=b,所以.
又因为四边形EFGH为矩形,
所以.
11.【答案】当Q为CC1的中点时,平面D1BQ∥平面PAO.
【解析】Q为CC1的中点.证明如下:
如图,设平面D1BQ∩平面ADD1A1=D1M,点M在AA1上,
由于平面D1BQ∩平面BCC1B1=BQ,平面ADD1A1∥平面BCC1B1,
由面面平行的性质定理可得BQ∥D1M.
12.【答案】证明详见解析.
【解析】∵,
∴和都是等边三角形,
∴.
如图,取的中点,连接,∴.
在中,,
∴,
∴.
在中,, ,
欢迎广大教师踊跃来稿,稿酬丰厚。 www.ks5u.com
欢迎广大教师踊跃来稿,稿酬丰厚。 www.ks5u.com
