四川省成都市高中数学 第三章 函数的应用综合检测 新人教A版必修1
文档属性
| 名称 | 四川省成都市高中数学 第三章 函数的应用综合检测 新人教A版必修1 |  | |
| 格式 | zip | ||
| 文件大小 | 682.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-25 08:57:33 | ||
图片预览




文档简介
第1课时 方程的根与函数的零点
基础达标(水平一)
1.函数f(x)=x-的零点是( ).
A.1 B.-1
C.1和-1 D.不存在
【解析】∵x-==0,∴x=±1.
【答案】C
2.函数f(x)=2x+3x的零点所在的一个区间是( ).
A.(-2,-1) B.(-1,0)
C.(0,1) D.(1,2)
【解析】∵f(x)为增函数,f(-1)=-<0,f(0)=1>0,
∴f(x)的零点位于区间(-1,0)内.
【答案】B
3.已知函数f(x)=则函数f(x)的零点为( ).
A.,0 B.-2,0
C. D.0
【解析】当x≤1时,由f(x)=0,得2x-1=0,所以x=0.当x>1时,由f(x)=0,得1+log2x=0,所以x=,不合题意,所以函数的零点为0,选D.
【答案】D
4.已知函数f(x)=(x-a)(x-b)-2,并且α,β是函数f(x)的两个零点,则实数a,b,α,β的大小关系可能是( ).
A.a<αC.α【解析】∵α,β是函数f(x)的两个零点,
∴f(α)=f(β)=0.
∵f(x)=(x-a)(x-b)-2,
∴f(a)=f(b)=-2<0.
结合二次函数f(x)的图象(如图)可知,a和b必在α与β之间,只有选项C满足.
【答案】C
5.根据表格中的数据,可以判断方程ex-x-2=0的一个根所在的区间是 .?
x
-1
0
1
2
3
ex
0.37
1
2.72
7.39
20.09
x+2
1
2
3
4
5
【解析】令f(x)=ex-x-2,则f(1)·f(2)<0,故方程ex-x-2=0的一个根所在的区间为(1,2).
【答案】(1,2)
6.方程ln x=8-2x的实数根x∈(k,k+1),k∈Z,则k= .?
【解析】令f(x)=ln x+2x-8,则f(x)在区间(0,+∞)内单调递增.
∵f(3)=ln 3-2<0,f(4)=ln 4>0,
∴函数f(x)的零点在(3,4)内,∴k=3.
【答案】3
7.已知方程ax2-2x+1=0的一个根在区间(0,1)上,另一个根在区间(1,2)上,求实数a的取值范围.
【解析】当a=0时,方程为-2x+1=0,只有一个根,不符合题意.
当a>0时,设f(x)=ax2-2x+1,
∵方程的根分别在区间(0,1),(1,2)上,
∴即解得当a<0时,设方程的两个根分别为x1,x2,
则x1·x2=<0,即x1,x2一正一负,不符合题意.
综上,实数a的取值范围为.
拓展提升(水平二)
8.已知f(x)是定义域为R的奇函数,且在(0,+∞)内的零点有1008个,则f(x)的零点的个数为( ).
A.1008 B.1009 C.2016 D.2017
【解析】因为f(x)为奇函数,且在(0,+∞)内有1008个零点,所以在(-∞,0)上也有1008个零点,又因为f(0)=0,所以共有2016+1=2017个零点.
【答案】D
9.方程0.9x-x=0的实数解的个数是( ).
A.0 B.1 C.2 D.3
【解析】设f(x)=0.9x-x,则f(x)为R上的减函数,且f(0)>0,f(21)<0,故方程0.9x-x=0的实数解的个数是1.
【答案】B
10.若函数f(x)唯一的零点在区间(1,3)或(1,4)或(1,5)内,则
①函数f(x)的零点在区间(1,2)或(2,3)内;
②函数f(x)在区间(3,5)内无零点;
③函数f(x)在区间(2,5)内有零点;
④函数f(x)在区间(2,4)内不一定有零点;
⑤函数f(x)的零点必在区间(1,5)内.
以上说法错误的是 .(将序号填在横线上)?
【解析】由于三个区间是包含关系,而(1,5)范围最大,故零点可能在区间(1,5)的任何一个子区间内,故①②③错误.
【答案】①②③
11.设函数g(x)=ax2+bx+c(a>0),且g(1)=-.
(1)求证:函数g(x)有两个零点.
(2)讨论函数g(x)在区间(0,2)内的零点个数.
【解析】(1)∵g(1)=a+b+c=-,
∴3a+2b+2c=0,∴c=-a-b.
∴g(x)=ax2+bx-a-b,∴Δ=b2+4a=(2a+b)2+2a2,
∵a>0,∴Δ>0恒成立,
故函数f(x)有两个零点.
(2)根据g(0)=c,g(2)=4a+2b+c,由(1)知3a+2b+2c=0,∴g(2)=a-c.
①当c>0时,有g(0)>0,又∵a>0,∴g(1)=-<0,
故函数g(x)在区间(0,1)内有一个零点,故在区间(0,2)内至少有一个零点.
②当c≤0时,g(1)<0,g(0)=c≤0,g(2)=a-c>0,
∴函数f(x)在区间(1,2)内有一个零点,
综合①②,可知函数g(x)在区间(0,2)内至少有一个零点.
第2课时 函数零点的应用
基础达标(水平一)
1.函数f(x)=的零点有( ).
A.0个 B.1个 C.2个 D.3个
【解析】由f(x)==0得x=1或x=-2(舍去),∴函数f(x)只有1个零点.
【答案】B
2.已知函数f(x)=若方程f(x)=k无实数根,则实数k的取值范围为( ).
A.kC.k< D.k≥
【解析】在同一平面直角坐标系内画出函数y=f(x)与y=k的图象如图所示,方程f(x)=k无实数根,即两个函数图象无交点,故k【答案】A
3.若函数f(x)是奇函数,且x0是y=f(x)+ex的一个零点,则-x0一定是下列哪个函数的零点( ).
A.y=f(-x)ex-1 B.y=f(x)e-x+1
C.y=exf(x)-1 D.y=exf(x)+1
【解析】由已知可得f(x0)=-,则f(x0)=-1,f(-x0)=1,故-x0一定是y=exf(x)-1的零点.
【答案】C
4.函数f(x)=ax2+bx+c,若f(1)>0,f(2)<0,则f(x)在区间(1,2)上( )零点.
A.至多有一个 B.有一个或两个
C.有且仅有一个 D.没有
【解析】若a=0,则b≠0,此时f(x)=bx+c为单调函数.
∵f(1)>0,f(2)<0,∴f(x)在区间(1,2)上有且仅有一个零点.
若a≠0,则f(x)为开口向上或向下的抛物线.若f(x)在区间(1,2)上有两个零点或无零点,则必有f(1)·f(2)>0.
∵f(1)>0,f(2)<0,∴f(x)在区间(1,2)上有且仅有一个零点,故选C.
【答案】C
5.若函数y=2-|x-1|-m有零点,则实数m的取值范围是 .?
【解析】由函数y=2-|x-1|=的图象(图略)可知0【答案】06.若函数f(x)=ax-x-a(a>0且a≠1)有两个零点,则实数a的取值范围是 .?
【解析】函数f(x)的零点的个数就是函数y=ax与函数y=x+a图象交点的个数,由函数的图象可知当a>1时,两函数图象有两个交点;当01.
【答案】(1,+∞)
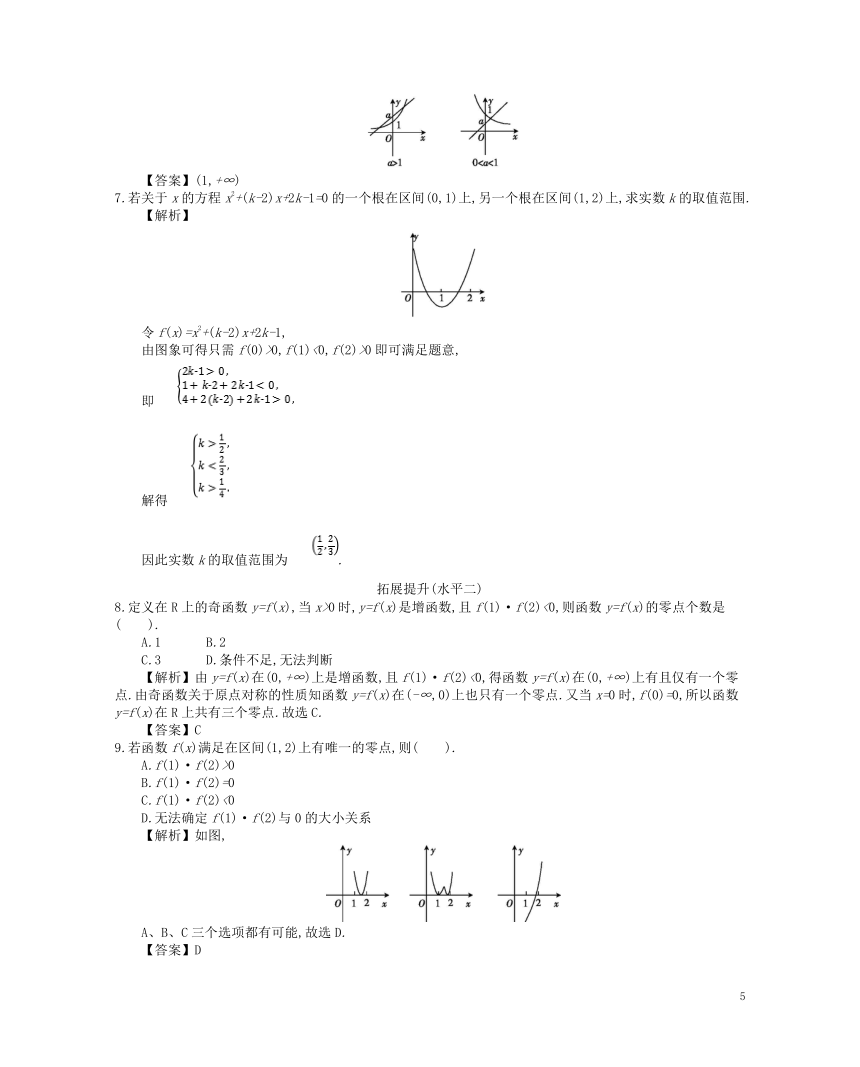
7.若关于x的方程x2+(k-2)x+2k-1=0的一个根在区间(0,1)上,另一个根在区间(1,2)上,求实数k的取值范围.
【解析】
令f(x)=x2+(k-2)x+2k-1,
由图象可得只需f(0)>0,f(1)<0,f(2)>0即可满足题意,
即
解得
因此实数k的取值范围为.
拓展提升(水平二)
8.定义在R上的奇函数y=f(x),当x>0时,y=f(x)是增函数,且f(1)·f(2)<0,则函数y=f(x)的零点个数是( ).
A.1 B.2
C.3 D.条件不足,无法判断
【解析】由y=f(x)在(0,+∞)上是增函数,且f(1)·f(2)<0,得函数y=f(x)在(0,+∞)上有且仅有一个零点.由奇函数关于原点对称的性质知函数y=f(x)在(-∞,0)上也只有一个零点.又当x=0时,f(0)=0,所以函数y=f(x)在R上共有三个零点.故选C.
【答案】C
9.若函数f(x)满足在区间(1,2)上有唯一的零点,则( ).
A.f(1)·f(2)>0
B.f(1)·f(2)=0
C.f(1)·f(2)<0
D.无法确定f(1)·f(2)与0的大小关系
【解析】如图,
A、B、C三个选项都有可能,故选D.
【答案】D
10.已知函数f(x)=|ln x|,g(x)=则方程|f(x)+g(x)|=1的实根个数为 .?
【解析】当0 当x>1时,f(x)+g(x)=ln x+x2-6单调递减,值域为(-5,+∞),方程f(x)+g(x)=1有1个解,方程f(x)+g(x)=-1有1个解.
综上所述,原方程有3个实根.
【答案】3
11.已知函数f(x)=x2-2x-3,x∈[-1,4].
(1)画出函数y=f(x)的图象,并写出其值域;
(2)当m为何值时,函数g(x)=f(x)+m在区间[-1,4]内有两个零点?
【解析】(1)依题意,f(x)=(x-1)2-4,x∈[-1,4],
其图象如图所示.
由图可知,函数f(x)的值域为[-4,5].
(2)∵函数g(x)=f(x)+m在区间[-1,4]上有两个零点,
∴方程f(x)=-m在x∈[-1,4]上有两个相异的实数根,
即函数y=f(x)与直线y=-m的图象有两个交点.
由(1)所作的图象可知,-4<-m≤0,∴0≤m<4.
∴当0≤m<4时,函数g(x)=f(x)+m在区间[-1,4]内有两个零点.
第3课时 用二分法求方程的近似解
基础达标(水平一)
1.若函数f(x)在[3,5]上连续,且满足f(3)·f(5)<0,取区间(3,5)内的中点值4之后,发现有f(3)·f(4)>0,则f(x)( ).
A.在[3,4]上有零点 B.在[4,5]上有零点
C.在[3,4]上无零点 D.在[4,5]上无零点
【解析】根据f(3)·f(4)>0无法判断函数f(x)在区间[3,4]上是否有零点,故排除A、C,但可推出f(4)·f(5)<0,所以可确定函数f(x)在区间[4,5]上有零点.
【答案】B
2.设函数f(x)=3x+3x-8,用二分法求方程3x+3x-8=0在x∈(1,2)内近似解的过程中得f(1)<0,f(1.5)>0,f(1.25)<0,则方程的根所在的区间为( )(区间长度0.25).
A.(1,1.25) B.(1,1.5)
C.(1.5,2) D.(1.25,1.5)
【解析】∵f(1)<0,f(1.25)<0,f(1.5)>0,∴方程的根落在(1.25,1.5)上.
【答案】D
3.用二分法求函数f(x)的一个正实数零点时,经计算f(0.64)<0,f(0.72)>0,f(0.68)<0,则函数的一个精确度为0.1的正实数零点的近似值为( ).
A.0.9 B.0.7 C.0.5 D.0.4
【解析】因为f(0.72)>0,f(0.68)<0,所以零点在区间(0.68,0.72)内,又|0.72-0.68|=0.04<0.1,所以零点在区间[0.68,0.72]内,故只有B选项符合要求.
【答案】B
4.在用二分法求函数f(x)在(a,b)上的唯一零点x0的过程中,取(a,b)上的中点c=,若f(c)=0,则函数f(x)在(a,b)上的唯一零点x0( ).
A.在(a,c)上 B.在(c,b)上
C.在(a,c)或(c,d)上 D.等于
【解析】∵c=,且f(c)=0,∴x0=.故选D.
【答案】D
5.已知函数f(x)=-log2x,若实数x0是方程-log2x=0的解,且0【解析】在同一平面直角坐标系中作出函数y=和y=log2x的图象(图略),发现x0>1,并且当00.
【答案】正
6.用二分法求连续函数f(x)=0在(1,5)上的近似解(精确度为0.1)的部分过程如下:f(1)·f(5)<0,取(1,5)的中点x1==3,计算得f(1)·f(x1)<0,f(x1)·f(5)>0,则此时能判断函数f(x)一定有零点的最小区间为 .?
【解析】因为函数f(x)为连续函数,且f(1)·f(3)<0,所以函数f(x)在区间(1,3)上一定有零点.
【答案】(1,3)
7.某娱乐节目有一个给选手在限定时间内猜一物品售价的环节,某次猜一品牌手机的价格,手机价格在500~1000元,选手开始报价1000元,主持人回答高了;紧接着报900元,高了;700元,低了;800元,低了;880元,高了;850元,低了;851元,恭喜你猜中了.表面上看猜价格具有很大的碰运气的成分,实际上体现了“逼近”的思想,试设计出可行的猜价方案.
【解析】取价格区间[500,1000]的中点750,低了;就再取[750,1000]的中点875,高了;就取[750,875]的中点,遇到小数,则取整数,照此猜下去可以猜价:750,875,812,843,859,851,经过6次即能猜中价格.
拓展提升(水平二)
8.用二分法求函数f(x)=ln x+2x-6在区间(2,3)内的零点近似值,至少经过( )次二分后精确度达到0.01.
A.5 B.6 C.7 D.8
【解析】区间(2,3)的长度等于1,每经过一次操作,区间长度变为原来的一半,经过n次操作后,区间长度变为,故有≤0.01,∴n≥7,∴至少需要操作7次.故选C.
【答案】C
9.已知曲线y=与y=x的交点的横坐标是x0,则x0的取值范围是( ).
A. B. C. D.(1,2)
【解析】设f(x)=-x,则函数f(x)为R上的减函数,f(0)=1>0,f=-<0,显然f(0)·f<0.所以x0的取值范围为.故选A.
【答案】A
10.某方程有一个无理根在区间D=(1,3)内,若用二分法求此根的近似值,将区间D等分 次后,所得近似值的精确度为0.1.?
【解析】由≤0.1(n∈N*),得2n≥20,∴n>4,故需将区间D等分5次.
【答案】5
11.如图,有一块边长为15 cm的正方形铁皮,将其四角各截去一个边长为x cm的小正方形,然后折成一个无盖的盒子.
(1)求盒子的容积y(以x为自变量)的函数解析式,并写出这个函数的定义域.
(2)如果要做一个容积为150 cm3的无盖盒子,那么截去的小正方形的边长x是多少(结果精确到0.1 cm)?
【解析】(1)盒子的容积y是以x为自变量的函数,解析式为y=x(15-2x)2,x∈(0,7.5).
(2)如果要做成一个容积是150 cm3的盒子,
则(15-2x)2·x=150.
令f(x)=(15-2x)2·x-150,由f(0)·f(1)<0,f(4)·f(5)<0,可以确定f(x)在(0,1)和(4,5)内各有一个零点,即方程(15-2x)2·x=150在区间(0,1)和(4,5)内各有一个解.
取区间(0,1)的中点x1=0.5,∵f(0.5)=-52,
∴零点x0∈(0.5,1).
再取中点x2=0.75,∵f(0.75)≈-13.31,∴零点x0∈(0.75,1).
继续有x0∈(0.75,0.875);x0∈(0.8125,0.875).
此时|0.875-0.8125|=0.0625<0.1,
∴方程在区间(0,1)内结果精确到0.1 cm的近似解为0.8.
同理,可得方程在区间(4,5)内精确度为0.1的近似解为4.7,所以要做成一个容积为150 cm3的无盖盒子,截去小正方形的边长大约是0.8 cm或4.7 cm.
第4课时 几类不同增长的函数模型
基础达标(水平一)
1.y1=2x,y2=x2,y3=log2x,当2A.y1>y2>y3 B.y2>y1>y3
C.y1>y3>y2 D.y2>y3>y1
【解析】在同一平面直角坐标系内画出这三个函数的图象(图略),在区间(2,4)内,从上到下图象依次对应的函数为y2=x2,y1=2x,y3=log2x,故y2>y1>y3.也可取特殊值,如3,代入即可.
【答案】B
2.在某种金属材料的耐高温实验中,温度随着时间变化的情况由微机记录后显示的图象如图所示.现给出下列说法:
①前5 min温度增加的速度越来越快;②前5 min温度增加的速度越来越慢;
③5 min以后温度保持匀速增加;
④5 min以后温度保持不变.
其中正确的说法是( ).
A.①③ B.②④ C.①④ D.②③
【解析】因为温度y关于时间t的图象是先凸后平,即5 min前每当t增加一个单位,y相应的增量越来越小,而5 min后y关于t的增量保持为0,故②④正确.
【答案】B
3.某商品降价20%,由于原材料上涨,欲恢复原价,则需提价( ).
A.10% B.15% C.20% D.25%
【解析】设该商品原价为a,需提价x,依题意得
a(1-0.2)(1+x)=a,
即0.8+0.8x=1,
得x=0.25=25%,故选D.
【答案】D
4.某林区的森林蓄积量每年比上一年平均增长10.4%,要增长到原来的x倍,需经过y年,则函数y=f(x)的图象大致为( ).
【解析】设该林区的森林原有蓄积量为a,由题意可得ax=a(1+0.104)y,故y=log1.104x(x≥1),函数为对数函数,所以函数y=f(x)的图象大致为D中图象,故选D.
【答案】D
5.某种动物的繁殖数量y(只)与时间x(年)的关系式为y=alog2(x+1),已知该动物第一年繁殖100只,则第15年会繁殖 只.?
【解析】由题意100=alog2(1+1),解得a=100,将x=15代入,得y=400.
【答案】400
6.下图表示一位骑自行车和一位骑摩托车的旅行者在相距80 km的甲、乙两城间从甲城行驶到乙城的路程与时间之间的函数关系,有人根据函数图象,提出了关于这两个旅行者的如下信息:
①骑自行车者比骑摩托车者早出发3 h,晚到1 h;
②骑自行车者是变速运动,骑摩托车者是匀速运动;
③骑摩托车者在出发1.5 h后追上了骑自行车者;
④骑摩托车者在出发1.5 h后与骑自行车者速度一样.
其中,正确信息的序号是 .?
【解析】看时间轴易知①正确;骑摩托车者行驶的路程与时间的函数图象是直线,所以是匀速运动,而骑自行车者行驶的路程与时间的函数图象是折线,所以是变速运动,因此②正确;两条曲线的交点的横坐标对应着4.5,故③正确;④错误.
【答案】①②③
7.某人对东北一种松树的生长情况进行了研究,收集了其高度h(米)与生长时间t(年)的相关数据,选择h=mt+b与h=loga(t+1)两种函数模型来刻画h与t的关系,你认为哪种函数模型更符合该松树的生长情况?并预测第8年的松树高度.
t(年)
1
2
3
4
5
6
h(米)
0.6
1
1.3
1.5
1.6
1.7
【解析】据表中数据作出散点图如图:
由图可以看出用一次函数模型不吻合,选用对数函数模型比较合理.
不妨将(2,1)代入到h=loga(t+1)中,得1=loga3,解得a=3.
故可用函数h=log3(t+1)来拟合这个实际问题.
当t=8时,求得h=log3(8+1)=2,
故可预测第8年松树的高度为2米.
拓展提升(水平二)
8.某公司为开发新产品,计划逐年加大研发资金的投入.若该公司2015年全年投入的研发资金为130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是( ).
(参考数据:lg 1.12≈0.05,lg 1.3≈0.11,lg 2≈0.30)
A.2018年 B.2019年 C.2020年 D.2021年
【解析】设第n年开始超过200万元,
则130×(1+12%)n-2015>200,
整理得(n-2015)lg 1.12>lg 2-lg 1.3,
n-2015>=3.8,故n=2019.
因此开始超过200万元的年份是2019年.故选B.
【答案】B
9.如图,点P在边长为1的正方形边上运动,设M为CD的中点,则当P沿ABCM运动时,点P经过的路程x与△APM的面积y之间的函数y=f(x)的图象大致是( ).
【解析】依题意,当0当1当2综上可知,选项A符合题意.
【答案】A
10.为了鼓励居民节约用水,我市某地水费按以下规定收取:
①当每户每月用水量不超过10吨(含10吨)时,水费单价3.20元/吨;
②当每户每月用水量超过10吨时,超过10吨的部分水费单价5.00元/吨.
(1)某用户某月用水量为x吨,需付水费为y元,则水费y (元)与用水量x (吨)之间的函数关系式为 ;?
(2)若小华家四月份付水费42元,问他家四月份用水 吨.?
【解析】(1)当0当x>10时,y=32+5(x-10).
即函数关系式为y=
(2)设小华家四月份用水量为x吨.
∵42>3.20×10,
∴小华家四月份用水量超过10吨,
由题意得3.20×10+(x-10)×5=42,
∴x=12(吨).即小华家四月份的用水量为12吨.
【答案】(1)y= (2)12
11.函数y=2x-2和y=x2的图象如图所示,其中有且只有x=x1,x2,x3时,两函数数值相等,且x1<0(1)请指出图中曲线C1,C2分别对应的函数;
(2)现给下列三个结论:
①当x∈(-∞,-1)时,2x-2②x2∈(1,2);
③x3?(4,5).
请你选择一个结论判定其是否成立,并说明理由.
【解析】(1)C1为y=x2,C2为y=2x-2.
(2)结论①成立,理由如下:
∵函数y=2x-2在(-∞,-1]上是增函数,
∴x∈(-∞,-1)时,2x-2<2-1-2=.
又∵函数y=x2在(-∞,-1]上是减函数,
∴x∈(-∞,-1)时,x2>×(-1)2=.
而<,∴当x∈(-∞,-1)时,2x-2结论②成立,理由如下:
构造函数f(x)=2x-2-x2,
则f(1)=>0,f(2)=-<0,
∴f(x)在区间(1,2)内有零点,
∴x2∈(1,2),同理f(x)在区间(5,6)内有零点,
∴x3∈(5,6).
结论③成立,理由同②.
第5课时 函数模型的应用实例
基础达标(水平一)
1.“弯弓射雕”描述了游牧民族的豪迈气概.当弓箭手以每秒a米的速度从地面垂直向上射箭时,t秒后的高度x米可由x=at-5t2确定.已知射出2秒后箭离地面高100米,则弓箭能达到的最大高度为( ).
A.160米 B.170米 C.180米 D.190米
【解析】由x=at-5t2且t=2时,x=100,解得a=60.所以x=60t-5t2.
由x=-5t2+60t=-5(t-6)2+180,
知当t=6时,x取得最大值为180,
即弓箭能达到的最大高度为180米.
【答案】C
2.某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表.那么各班可推选的代表人数y与该班人数x之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为( ).
A.y= B.y=
C.y= D.y=
【解析】当各班人数除以10的余数大于6时再增选一名代表,可以看作先用该班人数除以10再用这个余数与3相加,若和大于等于10就增选一名代表,将二者合并便得到推选代表人数y与该班人数x之间的函数关系,用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为y=.故选B.
【答案】B
3.马先生两年前购买了一部手机,现在这款手机的价格已降为1000元,设这款手机每年降价20%,那么两年前这部手机的价格为( ).
A.1535.5元 B.1440元
C.1620元 D.1562.5元
【解析】设这部手机两年前的价格为a元,则有a(1-0.2)2=1000,解得a=1562.5.
【答案】D
4.加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足的函数关系p=at2+bt+c(a,b,c是常数),右图记录了三次实验的数据,根据函数模型和实验数据,可以得到最佳加工时间为( ).
A.3.50分钟 B.3.75分钟
C.4.00分钟 D.4.25分钟
【解析】由图形可知,三点(3,0.7),(4,0.8),(5,0.5)都在函数p=at2+bt+c的图象上,所以解得a=-0.2,b=1.5,c=-2,
所以p=-0.2t2+1.5t-2=-0.2+,因为t>0,所以当t==3.75时,p取最大值,故此时的t=3.75分钟为最佳加工时间.
【答案】B
5.某商家将彩电价格先按原价提高40%,然后在广告上写上“大酬宾,八折优惠”,结果每台彩电比原价多赚270元,那么每台彩电的原价为 元.?
【解析】设原价为x元,则x(1+40%)·80%-x=270,解得x=2250.
【答案】2250
6.为了在“十一”黄金周期间降价促销,某超市对顾客实行购物优惠活动,规定一次购物付款总额:①如果不超过200元,则不予优惠;②如果超过200元,但不超过500元,则按标价给予9折优惠;③如果超过500元,其中500元按第②条给予优惠,超过500元的部分给予7折优惠.小云和她的母亲两次去购物,分别付款168元和423元,假设她们一次性购买上述同样的商品,则应付款额为 元.?
【解析】依题意,一次性购买x元商品和实际付款数f(x)之间的函数关系式为
f(x)=
当f(x)=168时,由168÷0.9≈187<200,故此时x=168;当f(x)=423时,由423÷0.9=470∈(200,500],故此时x=470.∴两次共购得价值为470+168=638元的商品,∴500×0.9+(638-500)×0.7=546.6元,故若一次性购买上述商品,应付款额为546.6元.
【答案】546.6
7.根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时,两类产品的收益分别为0.125万元和0.5万元(如图所示).
(1)分别写出两种产品的收益与投资额之间的函数关系式.
(2)若该家庭现有资金20万元,全部用于理财投资,问:怎样分配资金能使投资获得最大的收益?其最大收益为多少?
【解析】(1)设投资额为x万元,稳健型产品的收益为y1=f(x),风险型产品的收益为y2=g(x),
由题设知,f(x)=k1x,g(x)=k2,
由图①知,f(1)=,故k1=.
由图②知,g(1)=,故k2=.
所以f(x)=x(x≥0),g(x)=(x≥0).
(2)设该家庭债券类投资为x万元,股票类投资为(20-x)万元,
则y=f(x)+g(20-x)=+(0≤x≤20),
令t=(0≤t≤2),
则x=20-t2,y=+t=-(t2-4t-20)=-(t-2)2+3.
所以当t=2,即x=16时,ymax=3.
故当债券类投资为16万元,股票类投资为4万元时收益最大,最大收益为3万元.
拓展提升(水平二)
8.已知世界人口在过去40年内翻了一番,则每年人口的平均增长率约是( ).(参考数据:lg 2≈0.301,100.0075≈1.017)
A.1.5% B.1.6% C.1.7% D.1.8%
【解析】设每年人口的平均增长率是x,
由题意得,(1+x)40=2,则40lg(1+x)=lg 2,
即lg(1+x)=≈0.0075,所以x≈1.7%.
【答案】C
9.若某辆汽车每次加油都把油箱加满,下表记录了该车相邻两次加油时的情况.
加油时间
加油量/升
加油时的累计里程/千米
2018年5月1日
12
35000
2018年5月15日
48
35600
注:“累计里程”指汽车从出厂开始累计行驶的路程.
在这段时间内,该车每100千米平均耗油量为( ).
A.6升 B.8升 C.10升 D.12升
【解析】由表格信息可知,汽车行驶35600-35000=600千米耗油48升,所以每100千米的平均耗油量为8升,故选B.
【答案】B
10.某地区发生里氏8.0级特大地震.地震专家对发生的余震进行了监测,记录的部分数据如下表:
强度(J)
1.6×1019
3.2×1019
4.5×1019
6.4×1019
震级(里氏)
5.0
5.2
5.3
5.4
注:地震强度是指地震时释放的能量.
地震强度x和震级y的模拟函数关系可以选用y=alg x+b(a,b为常数).利用散点图可知a的值等于 .(取lg 2=0.3进行计算)?
【解析】由记录的部分数据可知,
当x=1.6×1019时,y=5,
当x=3.2×1019时,y=5.2,
所以5=alg(1.6×1019)+b, ①
5.2=alg(3.2×1019)+b, ②
由②-①得0.2=alg,
所以a===.
【答案】
11.某种特色水果每年的上市时间是从4月1日开始持续5个月的时间.上市初期价格呈现上涨趋势,中期价格开始下跌,后期价格在原有价格基础之上继续下跌.现有三种价格变化的模拟函数:①f(x)=p·qx;②f(x)=px2+qx+7;③f(x)=logq(x+p),其中p,q均为常数且q>1.(注:x表示上市时间,f(x)表示价格,记x=0表示4月1日,x=1表示5月1日,…,以此类推,x∈[0,5])
(1)在上述三个价格模拟函数中,哪一个更能体现该种水果的价格变化趋势?并简要说明理由.
(2)对(1)中所选的函数f(x),若f(2)=11,f(3)=10,记g(x)=,经过多年的统计发现,当函数g(x)取得最大值时,拓展外销市场的效果最为明显,请预测明年拓展外销市场的时间是几月1日?
【解析】(1)根据题意,该种水果的价格变化趋势是先增加后减少,基本符合开口向下的二次函数图象的变化趋势,故应该选择②.
(2)由f(2)=11,f(3)=10,
得解得
故f(x)=-x2+4x+7.
所以g(x)===-=-,此函数在[0,2]上单调递增,在[2,5]上单调递减,所以当x=2时,g(x)最大.
所以明年拓展外销市场的时间应为6月1日.
第三章章末小结
一、选择题
1.下列函数中,既是奇函数又有零点的增函数的是( ).
A.y= B.y=
C.y=log3x D.y=x3
【解析】A,C错,y=与y=log3x是非奇非偶函数;B是奇函数,但无零点,只有D正确.
【答案】D
2.下列关于函数f(x),x∈[a,b]的命题中,正确的是( ).
A.若x0∈[a,b]且满足f(x0)=0,则x0是f(x)的一个零点
B.若x0是f(x)在[a,b]上的零点,则可以用二分法求x0的近似值
C.函数f(x)的零点是方程f(x)=0的根,但f(x)=0的根不一定是函数f(x)的零点
D.用二分法求方程的根时,得到的都是近似解
【解析】选项A正确.使用“二分法”必须满足“二分法”的使用条件,选项B错误.f(x)=0的根也一定是函数f(x)的零点,选项C错误.用二分法求方程的根时,得到的也可能是精确解,选项D错误.故选A.
【答案】A
3.若函数f(x)=x2lg a-2x+1有两个零点,则实数a的取值范围是( ).
A.0 C.0【解析】lg a≠0且Δ=4-4lg a>0,解得0【答案】D
4.设函数y=x3与y=的图象的交点坐标为(x0,y0),则x0所在的区间是( ).
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
【解析】由题意知x0为方程x3=的根,令f(x)=x3-22-x,
∵f(0)=-4<0,f(1)=-1<0,f(2)=7>0,
∴x0∈(1,2).
【答案】B
5.如图,在直角梯形OABC中,AB∥OC,AB=1,OC=BC=2,直线l:x=t截此梯形所得位于l左方的图形面积为S,则函数S=f(t)的图象大致为( ).
【解析】由题意可得S=f(t)=?
∴函数S=f(t)的图象在[0,1]上为抛物线的一段,在(1,2]上为一条线段.
【答案】C
6.用二分法求方程f(x)=0在区间(1,2)内的唯一实数解x0时,经计算得f(1)=,f(2)=-5,f=9,则下列结论正确的是( ).
A.x0∈
B.x0=
C.x0∈
D.x0∈或x0∈
【解析】∵f(2)·f<0,∴x0∈.
【答案】C
7.已知函数f(x)=x2+2(m-1)x-5m-2,若函数f(x)的两个零点x1,x2满足x1<1,x2>1,则实数m的取值范围是( ).
A.(1,+∞) B.(-∞,1)
C.(-1,+∞) D.(-∞,-1)
【解析】函数f(x)=x2+2(m-1)x-5m-2开口向上,函数f(x)的两个零点x1,x2满足x1<1,x2>1,可得1+2(m-1)-5m-2<0,
解得m>-1.
【答案】C
8.函数f(x)=lg x-的零点所在的区间是( ).
A.(0,1) B.(1,10)
C.(10,100) D.(100,+∞)
【解析】∵f(1)=-1<0,f(10)=1-=>0,
∴f(1)·f(10)<0,由函数零点存在性定理知,函数f(x)=lg x-的零点所在的区间是(1,10),故选B.
【答案】B
9.已知a是函数f(x)的一个零点,且x1A.f(x1)·f(x2)>0 B.f(x1)·f(x2)<0
C.f(x1)·f(x2)≥0 D.以上都不对
【解析】定理的逆定理不成立,故f(x1)·f(x2)的值不确定.
【答案】D
10. 二次函数f(x)=ax2+bx+c的部分对应值如下表:
x
-3
-2
-1
0
1
2
3
4
f(x)
6
m
-4
-6
-6
-4
n
6
不求a,b,c的值,判断方程ax2+bx+c=0的两个根所在的区间是( ).
A.(-3,-1)和(2,4) B.(-3,-1)和(-1,1)
C.(-1,1)和(1,2) D.(-∞,-3)和(4,+∞)
【解析】因为f(-3)=6>0,f(-1)=-4<0,所以方程在区间(-3,-1)内必有根.又f(2)=-4<0,f(4)=6>0,所以方程在区间(2,4)内必有根.
【答案】A
11.函数f(x)=|x|+k有两个零点,则( ).
A.k=0 B.k>0 C.0≤k<1 D.k<0
【解析】在同一平面直角坐标系中作出函数y1=|x|和y2=-k的图象,如图所示.若函数f(x)有两个零点,则必有-k>0,即k<0.
【答案】D
12.设函数f(x)在(-∞,+∞)上有意义,对于给定的正数k,定义函数fk(x)=取k=,f(x)=,则fk(x)=的零点有( ).
A.0个 B.1个
C.2个 D.不确定,随k的变化而变化
【解析】取k=,f(x)=,则fk(x)=的图象如图所示.
则fk(x)=的零点就是fk(x)与y==的交点,故交点有两个,即零点有两个.
【答案】C
二、填空题
13.对于函数y=f(x),如果f(x0)=x0,我们就称实数x0是函数f(x)的不动点.设函数f(x)=3+log2x,则函数f(x)的不动点一共有 个.?
【解析】由题意得3+log2x=x,即log2x=x-3,
画出函数y=log2x和y=x-3的图象,如图所示.
结合图象,函数有2个交点,即函数f(x)的不动点一共有2个.
【答案】2
14.若函数f(x)=|2x-2|-b有两个零点,则实数b的取值范围是 .?
【解析】由f(x)=|2x-2|-b=0,得|2x-2|=b.
在同一平面直角坐标系中画出y=|2x-2|与y=b的图象(如图),
则当0【答案】(0,2)
15.已知函数y=lox与y=kx的图象有公共点A,且点A的横坐标为2,则k的值为 .?
【解析】当x=2时,y=lo2=-,
∵点在直线y=kx上,∴k=-.
【答案】-
16.函数f(x)=若关于x的方程f(x)=kx-k至少有两个不相等的实数根,则实数k的取值范围为 .?
【解析】由函数图象(图略)可知,当直线y=kx-k过点时,直线的斜率最小,即k=-;当直线y=kx-k与函数y=x2-x(x>0)相切时有一个交点,k=y'=1,故当函数f(x)与直线y=kx-k有两个不同的交点,即关于x的方程f(x)=kx-k至少有两个不相等的实数根时,则实数k的取值范围是∪(1,+∞).
【答案】∪(1,+∞)
三、解答题
17.若二次函数f(x)=-x2+2ax+4a+1的一个零点小于-1,另一个零点大于3,求实数a的取值范围.
【解析】因为二次函数f(x)=-x2+2ax+4a+1的图象开口向下,且在区间(-∞,-1)内与区间(3,+∞)内各有一个零点,所以
即
即解得a>.
故实数a的取值范围是.
18.已知函数f(x)=lg (a>0)为奇函数,函数g(x)=+b(b∈R).
(1)求a的值;
(2)若b>1,讨论方程g(x)=ln |x|实数根的个数.
【解析】(1)由f(x)=lg(a>0)为奇函数,得f(-x)+f(x)=0,
即lg +lg =lg =0,
所以=1,解得a=1(a=-1舍去).
(2)当b>1时,设h(x)=g(x)-ln |x|=+b-ln |x|,
则h(x)是偶函数且在(0,+∞)上单调递减,
又h(1)=2+b>0,h(e2b)=-b<-1<0,
所以h(x)在(0,+∞)上有唯一的零点,方程g(x)=ln |x|有2个实数根.
19.某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元.该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.
(1)当一次订购量为多少个时,零件的实际出厂单价恰好降为51元?
(2)设一次订购量为x个,零件的实际出厂单价为P元,写出P关于x的函数表达式.
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂单价-成本)
【解析】(1)设每个零件的实际出厂单价恰好降为51元时,一次订购量为x0个,则x0=100+=550.
因此,当一次订购量为550个时,每个零件的实际出厂单价恰好降为51元.
(2)当0当100当x≥550时,P=51.
所以P=f(x)=(x∈N).
(3)设销售商的一次订购量为x个时,工厂获得的利润为L元,
则L=(P-40)x=.
当x=500时,L=6000;
当x=1000时,L=11000.
因此,当销售商一次订购500个零件时,该厂获得的利润是6000元;
如果订购1000个,该厂获得的利润是11000元.
20.某公司制定了一个激励销售人员的奖励方案:当销售利润不超过10万元时,按销售利润的15%进行奖励;当销售利润超过10万元时,若超出A万元,则超出部分按2log5(A+1)进行奖励.记奖金为y(单位:万元),销售利润为x(单位:万元).
(1)写出奖金y关于销售利润x的关系式.
(2)如果业务员老江获得5.5万元的奖金,那么他的销售利润是多少万元?
【解析】(1)由题意知,y=
(2)由题意知,1.5+2log5(x-9)=5.5,
2log5(x-9)=4,
log5(x-9)=2,
得x-9=52,
解得x=34.
故业务员老江的销售利润是34万元.
21.某医药研究所开发一种新药,据监测,如果成人按规定的剂量服用,服用药后每毫升血液中的含药量y(微克)与服药的时间t(小时)之间的关系近似满足如图所示的曲线,其中OA是线段,曲线AB是函数y=kat(t≥1,a>0,且k,a是常数)的图象.
(1)写出服药后y关于t的函数关系式.
(2)据监测,每毫升血液中的含药量不少于2微克时治疗疾病有效.假设某人第一次服药为早上6:00,为保持疗效,第二次服药最迟应当在当天几点钟?
(3)若按(2)中的最迟时间服用第二次药,则第二次服药3小时后,该病人每毫升血液中的含药量为多少微克?(精确到0.1)
【解析】(1)当0≤t<1时,y=8t;
当t≥1时,由解得
∴y=
(2)由8×≥2,解得t≤5.∴第一次服药5小时后,即第二次服药最迟应当在当天上午11点钟服药.
(3)第二次服药3小时后,每毫升血液中含第一次所服药的药量为y1=8×=(微克),含第二次服药的药量为y2=8×=4(微克),∴y1+y2=+4≈4.7(微克).
故第二次服药3小时后,该病人每毫升血液中的含药量约为4.7微克.
22.已知函数f(x)=
(1)计算f的值;
(2)写出f(x)的单调区间;
(3)设函数g(x)=f(x)+c,若函数g(x)有三个零点,求实数c的取值范围.
【解析】(1)由已知得f=f(-2)=-2×(-2)2-4×(-2)+1=1.
所以f=f(1)=1+1=2.
(2)当x≤0时,函数f(x)=-2x2-4x+1=-2(x+1)2+3.
由函数的性质可知,f(x)在区间(-∞,-1)内单调递增,在区间[-1,0]内单调递减;
当x>0时,函数f(x)=x+1,显然f(x)在区间(0,+∞)上单调递增.
综上,f(x)的单调递增区间是(-∞,-1)和(0,+∞),单调递减区间是[-1,0].
(3)作出f(x)的图象,如图.
函数g(x)有三个零点,即方程f(x)+c=0有三个不同实根,
又方程f(x)+c=0等价于方程f(x)=-c,
所以当f(x)的图象与直线y=-c有三个交点时,
函数g(x)有三个零点.
数形结合得1<-c<3,即-3因此,函数g(x)有三个零点,实数c的取值范围是(-3,-1).
基础达标(水平一)
1.函数f(x)=x-的零点是( ).
A.1 B.-1
C.1和-1 D.不存在
【解析】∵x-==0,∴x=±1.
【答案】C
2.函数f(x)=2x+3x的零点所在的一个区间是( ).
A.(-2,-1) B.(-1,0)
C.(0,1) D.(1,2)
【解析】∵f(x)为增函数,f(-1)=-<0,f(0)=1>0,
∴f(x)的零点位于区间(-1,0)内.
【答案】B
3.已知函数f(x)=则函数f(x)的零点为( ).
A.,0 B.-2,0
C. D.0
【解析】当x≤1时,由f(x)=0,得2x-1=0,所以x=0.当x>1时,由f(x)=0,得1+log2x=0,所以x=,不合题意,所以函数的零点为0,选D.
【答案】D
4.已知函数f(x)=(x-a)(x-b)-2,并且α,β是函数f(x)的两个零点,则实数a,b,α,β的大小关系可能是( ).
A.a<α
∴f(α)=f(β)=0.
∵f(x)=(x-a)(x-b)-2,
∴f(a)=f(b)=-2<0.
结合二次函数f(x)的图象(如图)可知,a和b必在α与β之间,只有选项C满足.
【答案】C
5.根据表格中的数据,可以判断方程ex-x-2=0的一个根所在的区间是 .?
x
-1
0
1
2
3
ex
0.37
1
2.72
7.39
20.09
x+2
1
2
3
4
5
【解析】令f(x)=ex-x-2,则f(1)·f(2)<0,故方程ex-x-2=0的一个根所在的区间为(1,2).
【答案】(1,2)
6.方程ln x=8-2x的实数根x∈(k,k+1),k∈Z,则k= .?
【解析】令f(x)=ln x+2x-8,则f(x)在区间(0,+∞)内单调递增.
∵f(3)=ln 3-2<0,f(4)=ln 4>0,
∴函数f(x)的零点在(3,4)内,∴k=3.
【答案】3
7.已知方程ax2-2x+1=0的一个根在区间(0,1)上,另一个根在区间(1,2)上,求实数a的取值范围.
【解析】当a=0时,方程为-2x+1=0,只有一个根,不符合题意.
当a>0时,设f(x)=ax2-2x+1,
∵方程的根分别在区间(0,1),(1,2)上,
∴即解得
则x1·x2=<0,即x1,x2一正一负,不符合题意.
综上,实数a的取值范围为.
拓展提升(水平二)
8.已知f(x)是定义域为R的奇函数,且在(0,+∞)内的零点有1008个,则f(x)的零点的个数为( ).
A.1008 B.1009 C.2016 D.2017
【解析】因为f(x)为奇函数,且在(0,+∞)内有1008个零点,所以在(-∞,0)上也有1008个零点,又因为f(0)=0,所以共有2016+1=2017个零点.
【答案】D
9.方程0.9x-x=0的实数解的个数是( ).
A.0 B.1 C.2 D.3
【解析】设f(x)=0.9x-x,则f(x)为R上的减函数,且f(0)>0,f(21)<0,故方程0.9x-x=0的实数解的个数是1.
【答案】B
10.若函数f(x)唯一的零点在区间(1,3)或(1,4)或(1,5)内,则
①函数f(x)的零点在区间(1,2)或(2,3)内;
②函数f(x)在区间(3,5)内无零点;
③函数f(x)在区间(2,5)内有零点;
④函数f(x)在区间(2,4)内不一定有零点;
⑤函数f(x)的零点必在区间(1,5)内.
以上说法错误的是 .(将序号填在横线上)?
【解析】由于三个区间是包含关系,而(1,5)范围最大,故零点可能在区间(1,5)的任何一个子区间内,故①②③错误.
【答案】①②③
11.设函数g(x)=ax2+bx+c(a>0),且g(1)=-.
(1)求证:函数g(x)有两个零点.
(2)讨论函数g(x)在区间(0,2)内的零点个数.
【解析】(1)∵g(1)=a+b+c=-,
∴3a+2b+2c=0,∴c=-a-b.
∴g(x)=ax2+bx-a-b,∴Δ=b2+4a=(2a+b)2+2a2,
∵a>0,∴Δ>0恒成立,
故函数f(x)有两个零点.
(2)根据g(0)=c,g(2)=4a+2b+c,由(1)知3a+2b+2c=0,∴g(2)=a-c.
①当c>0时,有g(0)>0,又∵a>0,∴g(1)=-<0,
故函数g(x)在区间(0,1)内有一个零点,故在区间(0,2)内至少有一个零点.
②当c≤0时,g(1)<0,g(0)=c≤0,g(2)=a-c>0,
∴函数f(x)在区间(1,2)内有一个零点,
综合①②,可知函数g(x)在区间(0,2)内至少有一个零点.
第2课时 函数零点的应用
基础达标(水平一)
1.函数f(x)=的零点有( ).
A.0个 B.1个 C.2个 D.3个
【解析】由f(x)==0得x=1或x=-2(舍去),∴函数f(x)只有1个零点.
【答案】B
2.已知函数f(x)=若方程f(x)=k无实数根,则实数k的取值范围为( ).
A.k
【解析】在同一平面直角坐标系内画出函数y=f(x)与y=k的图象如图所示,方程f(x)=k无实数根,即两个函数图象无交点,故k
3.若函数f(x)是奇函数,且x0是y=f(x)+ex的一个零点,则-x0一定是下列哪个函数的零点( ).
A.y=f(-x)ex-1 B.y=f(x)e-x+1
C.y=exf(x)-1 D.y=exf(x)+1
【解析】由已知可得f(x0)=-,则f(x0)=-1,f(-x0)=1,故-x0一定是y=exf(x)-1的零点.
【答案】C
4.函数f(x)=ax2+bx+c,若f(1)>0,f(2)<0,则f(x)在区间(1,2)上( )零点.
A.至多有一个 B.有一个或两个
C.有且仅有一个 D.没有
【解析】若a=0,则b≠0,此时f(x)=bx+c为单调函数.
∵f(1)>0,f(2)<0,∴f(x)在区间(1,2)上有且仅有一个零点.
若a≠0,则f(x)为开口向上或向下的抛物线.若f(x)在区间(1,2)上有两个零点或无零点,则必有f(1)·f(2)>0.
∵f(1)>0,f(2)<0,∴f(x)在区间(1,2)上有且仅有一个零点,故选C.
【答案】C
5.若函数y=2-|x-1|-m有零点,则实数m的取值范围是 .?
【解析】由函数y=2-|x-1|=的图象(图略)可知0
【解析】函数f(x)的零点的个数就是函数y=ax与函数y=x+a图象交点的个数,由函数的图象可知当a>1时,两函数图象有两个交点;当0
【答案】(1,+∞)
7.若关于x的方程x2+(k-2)x+2k-1=0的一个根在区间(0,1)上,另一个根在区间(1,2)上,求实数k的取值范围.
【解析】
令f(x)=x2+(k-2)x+2k-1,
由图象可得只需f(0)>0,f(1)<0,f(2)>0即可满足题意,
即
解得
因此实数k的取值范围为.
拓展提升(水平二)
8.定义在R上的奇函数y=f(x),当x>0时,y=f(x)是增函数,且f(1)·f(2)<0,则函数y=f(x)的零点个数是( ).
A.1 B.2
C.3 D.条件不足,无法判断
【解析】由y=f(x)在(0,+∞)上是增函数,且f(1)·f(2)<0,得函数y=f(x)在(0,+∞)上有且仅有一个零点.由奇函数关于原点对称的性质知函数y=f(x)在(-∞,0)上也只有一个零点.又当x=0时,f(0)=0,所以函数y=f(x)在R上共有三个零点.故选C.
【答案】C
9.若函数f(x)满足在区间(1,2)上有唯一的零点,则( ).
A.f(1)·f(2)>0
B.f(1)·f(2)=0
C.f(1)·f(2)<0
D.无法确定f(1)·f(2)与0的大小关系
【解析】如图,
A、B、C三个选项都有可能,故选D.
【答案】D
10.已知函数f(x)=|ln x|,g(x)=则方程|f(x)+g(x)|=1的实根个数为 .?
【解析】当0
综上所述,原方程有3个实根.
【答案】3
11.已知函数f(x)=x2-2x-3,x∈[-1,4].
(1)画出函数y=f(x)的图象,并写出其值域;
(2)当m为何值时,函数g(x)=f(x)+m在区间[-1,4]内有两个零点?
【解析】(1)依题意,f(x)=(x-1)2-4,x∈[-1,4],
其图象如图所示.
由图可知,函数f(x)的值域为[-4,5].
(2)∵函数g(x)=f(x)+m在区间[-1,4]上有两个零点,
∴方程f(x)=-m在x∈[-1,4]上有两个相异的实数根,
即函数y=f(x)与直线y=-m的图象有两个交点.
由(1)所作的图象可知,-4<-m≤0,∴0≤m<4.
∴当0≤m<4时,函数g(x)=f(x)+m在区间[-1,4]内有两个零点.
第3课时 用二分法求方程的近似解
基础达标(水平一)
1.若函数f(x)在[3,5]上连续,且满足f(3)·f(5)<0,取区间(3,5)内的中点值4之后,发现有f(3)·f(4)>0,则f(x)( ).
A.在[3,4]上有零点 B.在[4,5]上有零点
C.在[3,4]上无零点 D.在[4,5]上无零点
【解析】根据f(3)·f(4)>0无法判断函数f(x)在区间[3,4]上是否有零点,故排除A、C,但可推出f(4)·f(5)<0,所以可确定函数f(x)在区间[4,5]上有零点.
【答案】B
2.设函数f(x)=3x+3x-8,用二分法求方程3x+3x-8=0在x∈(1,2)内近似解的过程中得f(1)<0,f(1.5)>0,f(1.25)<0,则方程的根所在的区间为( )(区间长度0.25).
A.(1,1.25) B.(1,1.5)
C.(1.5,2) D.(1.25,1.5)
【解析】∵f(1)<0,f(1.25)<0,f(1.5)>0,∴方程的根落在(1.25,1.5)上.
【答案】D
3.用二分法求函数f(x)的一个正实数零点时,经计算f(0.64)<0,f(0.72)>0,f(0.68)<0,则函数的一个精确度为0.1的正实数零点的近似值为( ).
A.0.9 B.0.7 C.0.5 D.0.4
【解析】因为f(0.72)>0,f(0.68)<0,所以零点在区间(0.68,0.72)内,又|0.72-0.68|=0.04<0.1,所以零点在区间[0.68,0.72]内,故只有B选项符合要求.
【答案】B
4.在用二分法求函数f(x)在(a,b)上的唯一零点x0的过程中,取(a,b)上的中点c=,若f(c)=0,则函数f(x)在(a,b)上的唯一零点x0( ).
A.在(a,c)上 B.在(c,b)上
C.在(a,c)或(c,d)上 D.等于
【解析】∵c=,且f(c)=0,∴x0=.故选D.
【答案】D
5.已知函数f(x)=-log2x,若实数x0是方程-log2x=0的解,且0
【答案】正
6.用二分法求连续函数f(x)=0在(1,5)上的近似解(精确度为0.1)的部分过程如下:f(1)·f(5)<0,取(1,5)的中点x1==3,计算得f(1)·f(x1)<0,f(x1)·f(5)>0,则此时能判断函数f(x)一定有零点的最小区间为 .?
【解析】因为函数f(x)为连续函数,且f(1)·f(3)<0,所以函数f(x)在区间(1,3)上一定有零点.
【答案】(1,3)
7.某娱乐节目有一个给选手在限定时间内猜一物品售价的环节,某次猜一品牌手机的价格,手机价格在500~1000元,选手开始报价1000元,主持人回答高了;紧接着报900元,高了;700元,低了;800元,低了;880元,高了;850元,低了;851元,恭喜你猜中了.表面上看猜价格具有很大的碰运气的成分,实际上体现了“逼近”的思想,试设计出可行的猜价方案.
【解析】取价格区间[500,1000]的中点750,低了;就再取[750,1000]的中点875,高了;就取[750,875]的中点,遇到小数,则取整数,照此猜下去可以猜价:750,875,812,843,859,851,经过6次即能猜中价格.
拓展提升(水平二)
8.用二分法求函数f(x)=ln x+2x-6在区间(2,3)内的零点近似值,至少经过( )次二分后精确度达到0.01.
A.5 B.6 C.7 D.8
【解析】区间(2,3)的长度等于1,每经过一次操作,区间长度变为原来的一半,经过n次操作后,区间长度变为,故有≤0.01,∴n≥7,∴至少需要操作7次.故选C.
【答案】C
9.已知曲线y=与y=x的交点的横坐标是x0,则x0的取值范围是( ).
A. B. C. D.(1,2)
【解析】设f(x)=-x,则函数f(x)为R上的减函数,f(0)=1>0,f=-<0,显然f(0)·f<0.所以x0的取值范围为.故选A.
【答案】A
10.某方程有一个无理根在区间D=(1,3)内,若用二分法求此根的近似值,将区间D等分 次后,所得近似值的精确度为0.1.?
【解析】由≤0.1(n∈N*),得2n≥20,∴n>4,故需将区间D等分5次.
【答案】5
11.如图,有一块边长为15 cm的正方形铁皮,将其四角各截去一个边长为x cm的小正方形,然后折成一个无盖的盒子.
(1)求盒子的容积y(以x为自变量)的函数解析式,并写出这个函数的定义域.
(2)如果要做一个容积为150 cm3的无盖盒子,那么截去的小正方形的边长x是多少(结果精确到0.1 cm)?
【解析】(1)盒子的容积y是以x为自变量的函数,解析式为y=x(15-2x)2,x∈(0,7.5).
(2)如果要做成一个容积是150 cm3的盒子,
则(15-2x)2·x=150.
令f(x)=(15-2x)2·x-150,由f(0)·f(1)<0,f(4)·f(5)<0,可以确定f(x)在(0,1)和(4,5)内各有一个零点,即方程(15-2x)2·x=150在区间(0,1)和(4,5)内各有一个解.
取区间(0,1)的中点x1=0.5,∵f(0.5)=-52,
∴零点x0∈(0.5,1).
再取中点x2=0.75,∵f(0.75)≈-13.31,∴零点x0∈(0.75,1).
继续有x0∈(0.75,0.875);x0∈(0.8125,0.875).
此时|0.875-0.8125|=0.0625<0.1,
∴方程在区间(0,1)内结果精确到0.1 cm的近似解为0.8.
同理,可得方程在区间(4,5)内精确度为0.1的近似解为4.7,所以要做成一个容积为150 cm3的无盖盒子,截去小正方形的边长大约是0.8 cm或4.7 cm.
第4课时 几类不同增长的函数模型
基础达标(水平一)
1.y1=2x,y2=x2,y3=log2x,当2
C.y1>y3>y2 D.y2>y3>y1
【解析】在同一平面直角坐标系内画出这三个函数的图象(图略),在区间(2,4)内,从上到下图象依次对应的函数为y2=x2,y1=2x,y3=log2x,故y2>y1>y3.也可取特殊值,如3,代入即可.
【答案】B
2.在某种金属材料的耐高温实验中,温度随着时间变化的情况由微机记录后显示的图象如图所示.现给出下列说法:
①前5 min温度增加的速度越来越快;②前5 min温度增加的速度越来越慢;
③5 min以后温度保持匀速增加;
④5 min以后温度保持不变.
其中正确的说法是( ).
A.①③ B.②④ C.①④ D.②③
【解析】因为温度y关于时间t的图象是先凸后平,即5 min前每当t增加一个单位,y相应的增量越来越小,而5 min后y关于t的增量保持为0,故②④正确.
【答案】B
3.某商品降价20%,由于原材料上涨,欲恢复原价,则需提价( ).
A.10% B.15% C.20% D.25%
【解析】设该商品原价为a,需提价x,依题意得
a(1-0.2)(1+x)=a,
即0.8+0.8x=1,
得x=0.25=25%,故选D.
【答案】D
4.某林区的森林蓄积量每年比上一年平均增长10.4%,要增长到原来的x倍,需经过y年,则函数y=f(x)的图象大致为( ).
【解析】设该林区的森林原有蓄积量为a,由题意可得ax=a(1+0.104)y,故y=log1.104x(x≥1),函数为对数函数,所以函数y=f(x)的图象大致为D中图象,故选D.
【答案】D
5.某种动物的繁殖数量y(只)与时间x(年)的关系式为y=alog2(x+1),已知该动物第一年繁殖100只,则第15年会繁殖 只.?
【解析】由题意100=alog2(1+1),解得a=100,将x=15代入,得y=400.
【答案】400
6.下图表示一位骑自行车和一位骑摩托车的旅行者在相距80 km的甲、乙两城间从甲城行驶到乙城的路程与时间之间的函数关系,有人根据函数图象,提出了关于这两个旅行者的如下信息:
①骑自行车者比骑摩托车者早出发3 h,晚到1 h;
②骑自行车者是变速运动,骑摩托车者是匀速运动;
③骑摩托车者在出发1.5 h后追上了骑自行车者;
④骑摩托车者在出发1.5 h后与骑自行车者速度一样.
其中,正确信息的序号是 .?
【解析】看时间轴易知①正确;骑摩托车者行驶的路程与时间的函数图象是直线,所以是匀速运动,而骑自行车者行驶的路程与时间的函数图象是折线,所以是变速运动,因此②正确;两条曲线的交点的横坐标对应着4.5,故③正确;④错误.
【答案】①②③
7.某人对东北一种松树的生长情况进行了研究,收集了其高度h(米)与生长时间t(年)的相关数据,选择h=mt+b与h=loga(t+1)两种函数模型来刻画h与t的关系,你认为哪种函数模型更符合该松树的生长情况?并预测第8年的松树高度.
t(年)
1
2
3
4
5
6
h(米)
0.6
1
1.3
1.5
1.6
1.7
【解析】据表中数据作出散点图如图:
由图可以看出用一次函数模型不吻合,选用对数函数模型比较合理.
不妨将(2,1)代入到h=loga(t+1)中,得1=loga3,解得a=3.
故可用函数h=log3(t+1)来拟合这个实际问题.
当t=8时,求得h=log3(8+1)=2,
故可预测第8年松树的高度为2米.
拓展提升(水平二)
8.某公司为开发新产品,计划逐年加大研发资金的投入.若该公司2015年全年投入的研发资金为130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是( ).
(参考数据:lg 1.12≈0.05,lg 1.3≈0.11,lg 2≈0.30)
A.2018年 B.2019年 C.2020年 D.2021年
【解析】设第n年开始超过200万元,
则130×(1+12%)n-2015>200,
整理得(n-2015)lg 1.12>lg 2-lg 1.3,
n-2015>=3.8,故n=2019.
因此开始超过200万元的年份是2019年.故选B.
【答案】B
9.如图,点P在边长为1的正方形边上运动,设M为CD的中点,则当P沿ABCM运动时,点P经过的路程x与△APM的面积y之间的函数y=f(x)的图象大致是( ).
【解析】依题意,当0
【答案】A
10.为了鼓励居民节约用水,我市某地水费按以下规定收取:
①当每户每月用水量不超过10吨(含10吨)时,水费单价3.20元/吨;
②当每户每月用水量超过10吨时,超过10吨的部分水费单价5.00元/吨.
(1)某用户某月用水量为x吨,需付水费为y元,则水费y (元)与用水量x (吨)之间的函数关系式为 ;?
(2)若小华家四月份付水费42元,问他家四月份用水 吨.?
【解析】(1)当0
即函数关系式为y=
(2)设小华家四月份用水量为x吨.
∵42>3.20×10,
∴小华家四月份用水量超过10吨,
由题意得3.20×10+(x-10)×5=42,
∴x=12(吨).即小华家四月份的用水量为12吨.
【答案】(1)y= (2)12
11.函数y=2x-2和y=x2的图象如图所示,其中有且只有x=x1,x2,x3时,两函数数值相等,且x1<0
(2)现给下列三个结论:
①当x∈(-∞,-1)时,2x-2
③x3?(4,5).
请你选择一个结论判定其是否成立,并说明理由.
【解析】(1)C1为y=x2,C2为y=2x-2.
(2)结论①成立,理由如下:
∵函数y=2x-2在(-∞,-1]上是增函数,
∴x∈(-∞,-1)时,2x-2<2-1-2=.
又∵函数y=x2在(-∞,-1]上是减函数,
∴x∈(-∞,-1)时,x2>×(-1)2=.
而<,∴当x∈(-∞,-1)时,2x-2
构造函数f(x)=2x-2-x2,
则f(1)=>0,f(2)=-<0,
∴f(x)在区间(1,2)内有零点,
∴x2∈(1,2),同理f(x)在区间(5,6)内有零点,
∴x3∈(5,6).
结论③成立,理由同②.
第5课时 函数模型的应用实例
基础达标(水平一)
1.“弯弓射雕”描述了游牧民族的豪迈气概.当弓箭手以每秒a米的速度从地面垂直向上射箭时,t秒后的高度x米可由x=at-5t2确定.已知射出2秒后箭离地面高100米,则弓箭能达到的最大高度为( ).
A.160米 B.170米 C.180米 D.190米
【解析】由x=at-5t2且t=2时,x=100,解得a=60.所以x=60t-5t2.
由x=-5t2+60t=-5(t-6)2+180,
知当t=6时,x取得最大值为180,
即弓箭能达到的最大高度为180米.
【答案】C
2.某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表.那么各班可推选的代表人数y与该班人数x之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为( ).
A.y= B.y=
C.y= D.y=
【解析】当各班人数除以10的余数大于6时再增选一名代表,可以看作先用该班人数除以10再用这个余数与3相加,若和大于等于10就增选一名代表,将二者合并便得到推选代表人数y与该班人数x之间的函数关系,用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为y=.故选B.
【答案】B
3.马先生两年前购买了一部手机,现在这款手机的价格已降为1000元,设这款手机每年降价20%,那么两年前这部手机的价格为( ).
A.1535.5元 B.1440元
C.1620元 D.1562.5元
【解析】设这部手机两年前的价格为a元,则有a(1-0.2)2=1000,解得a=1562.5.
【答案】D
4.加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足的函数关系p=at2+bt+c(a,b,c是常数),右图记录了三次实验的数据,根据函数模型和实验数据,可以得到最佳加工时间为( ).
A.3.50分钟 B.3.75分钟
C.4.00分钟 D.4.25分钟
【解析】由图形可知,三点(3,0.7),(4,0.8),(5,0.5)都在函数p=at2+bt+c的图象上,所以解得a=-0.2,b=1.5,c=-2,
所以p=-0.2t2+1.5t-2=-0.2+,因为t>0,所以当t==3.75时,p取最大值,故此时的t=3.75分钟为最佳加工时间.
【答案】B
5.某商家将彩电价格先按原价提高40%,然后在广告上写上“大酬宾,八折优惠”,结果每台彩电比原价多赚270元,那么每台彩电的原价为 元.?
【解析】设原价为x元,则x(1+40%)·80%-x=270,解得x=2250.
【答案】2250
6.为了在“十一”黄金周期间降价促销,某超市对顾客实行购物优惠活动,规定一次购物付款总额:①如果不超过200元,则不予优惠;②如果超过200元,但不超过500元,则按标价给予9折优惠;③如果超过500元,其中500元按第②条给予优惠,超过500元的部分给予7折优惠.小云和她的母亲两次去购物,分别付款168元和423元,假设她们一次性购买上述同样的商品,则应付款额为 元.?
【解析】依题意,一次性购买x元商品和实际付款数f(x)之间的函数关系式为
f(x)=
当f(x)=168时,由168÷0.9≈187<200,故此时x=168;当f(x)=423时,由423÷0.9=470∈(200,500],故此时x=470.∴两次共购得价值为470+168=638元的商品,∴500×0.9+(638-500)×0.7=546.6元,故若一次性购买上述商品,应付款额为546.6元.
【答案】546.6
7.根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时,两类产品的收益分别为0.125万元和0.5万元(如图所示).
(1)分别写出两种产品的收益与投资额之间的函数关系式.
(2)若该家庭现有资金20万元,全部用于理财投资,问:怎样分配资金能使投资获得最大的收益?其最大收益为多少?
【解析】(1)设投资额为x万元,稳健型产品的收益为y1=f(x),风险型产品的收益为y2=g(x),
由题设知,f(x)=k1x,g(x)=k2,
由图①知,f(1)=,故k1=.
由图②知,g(1)=,故k2=.
所以f(x)=x(x≥0),g(x)=(x≥0).
(2)设该家庭债券类投资为x万元,股票类投资为(20-x)万元,
则y=f(x)+g(20-x)=+(0≤x≤20),
令t=(0≤t≤2),
则x=20-t2,y=+t=-(t2-4t-20)=-(t-2)2+3.
所以当t=2,即x=16时,ymax=3.
故当债券类投资为16万元,股票类投资为4万元时收益最大,最大收益为3万元.
拓展提升(水平二)
8.已知世界人口在过去40年内翻了一番,则每年人口的平均增长率约是( ).(参考数据:lg 2≈0.301,100.0075≈1.017)
A.1.5% B.1.6% C.1.7% D.1.8%
【解析】设每年人口的平均增长率是x,
由题意得,(1+x)40=2,则40lg(1+x)=lg 2,
即lg(1+x)=≈0.0075,所以x≈1.7%.
【答案】C
9.若某辆汽车每次加油都把油箱加满,下表记录了该车相邻两次加油时的情况.
加油时间
加油量/升
加油时的累计里程/千米
2018年5月1日
12
35000
2018年5月15日
48
35600
注:“累计里程”指汽车从出厂开始累计行驶的路程.
在这段时间内,该车每100千米平均耗油量为( ).
A.6升 B.8升 C.10升 D.12升
【解析】由表格信息可知,汽车行驶35600-35000=600千米耗油48升,所以每100千米的平均耗油量为8升,故选B.
【答案】B
10.某地区发生里氏8.0级特大地震.地震专家对发生的余震进行了监测,记录的部分数据如下表:
强度(J)
1.6×1019
3.2×1019
4.5×1019
6.4×1019
震级(里氏)
5.0
5.2
5.3
5.4
注:地震强度是指地震时释放的能量.
地震强度x和震级y的模拟函数关系可以选用y=alg x+b(a,b为常数).利用散点图可知a的值等于 .(取lg 2=0.3进行计算)?
【解析】由记录的部分数据可知,
当x=1.6×1019时,y=5,
当x=3.2×1019时,y=5.2,
所以5=alg(1.6×1019)+b, ①
5.2=alg(3.2×1019)+b, ②
由②-①得0.2=alg,
所以a===.
【答案】
11.某种特色水果每年的上市时间是从4月1日开始持续5个月的时间.上市初期价格呈现上涨趋势,中期价格开始下跌,后期价格在原有价格基础之上继续下跌.现有三种价格变化的模拟函数:①f(x)=p·qx;②f(x)=px2+qx+7;③f(x)=logq(x+p),其中p,q均为常数且q>1.(注:x表示上市时间,f(x)表示价格,记x=0表示4月1日,x=1表示5月1日,…,以此类推,x∈[0,5])
(1)在上述三个价格模拟函数中,哪一个更能体现该种水果的价格变化趋势?并简要说明理由.
(2)对(1)中所选的函数f(x),若f(2)=11,f(3)=10,记g(x)=,经过多年的统计发现,当函数g(x)取得最大值时,拓展外销市场的效果最为明显,请预测明年拓展外销市场的时间是几月1日?
【解析】(1)根据题意,该种水果的价格变化趋势是先增加后减少,基本符合开口向下的二次函数图象的变化趋势,故应该选择②.
(2)由f(2)=11,f(3)=10,
得解得
故f(x)=-x2+4x+7.
所以g(x)===-=-,此函数在[0,2]上单调递增,在[2,5]上单调递减,所以当x=2时,g(x)最大.
所以明年拓展外销市场的时间应为6月1日.
第三章章末小结
一、选择题
1.下列函数中,既是奇函数又有零点的增函数的是( ).
A.y= B.y=
C.y=log3x D.y=x3
【解析】A,C错,y=与y=log3x是非奇非偶函数;B是奇函数,但无零点,只有D正确.
【答案】D
2.下列关于函数f(x),x∈[a,b]的命题中,正确的是( ).
A.若x0∈[a,b]且满足f(x0)=0,则x0是f(x)的一个零点
B.若x0是f(x)在[a,b]上的零点,则可以用二分法求x0的近似值
C.函数f(x)的零点是方程f(x)=0的根,但f(x)=0的根不一定是函数f(x)的零点
D.用二分法求方程的根时,得到的都是近似解
【解析】选项A正确.使用“二分法”必须满足“二分法”的使用条件,选项B错误.f(x)=0的根也一定是函数f(x)的零点,选项C错误.用二分法求方程的根时,得到的也可能是精确解,选项D错误.故选A.
【答案】A
3.若函数f(x)=x2lg a-2x+1有两个零点,则实数a的取值范围是( ).
A.0
4.设函数y=x3与y=的图象的交点坐标为(x0,y0),则x0所在的区间是( ).
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
【解析】由题意知x0为方程x3=的根,令f(x)=x3-22-x,
∵f(0)=-4<0,f(1)=-1<0,f(2)=7>0,
∴x0∈(1,2).
【答案】B
5.如图,在直角梯形OABC中,AB∥OC,AB=1,OC=BC=2,直线l:x=t截此梯形所得位于l左方的图形面积为S,则函数S=f(t)的图象大致为( ).
【解析】由题意可得S=f(t)=?
∴函数S=f(t)的图象在[0,1]上为抛物线的一段,在(1,2]上为一条线段.
【答案】C
6.用二分法求方程f(x)=0在区间(1,2)内的唯一实数解x0时,经计算得f(1)=,f(2)=-5,f=9,则下列结论正确的是( ).
A.x0∈
B.x0=
C.x0∈
D.x0∈或x0∈
【解析】∵f(2)·f<0,∴x0∈.
【答案】C
7.已知函数f(x)=x2+2(m-1)x-5m-2,若函数f(x)的两个零点x1,x2满足x1<1,x2>1,则实数m的取值范围是( ).
A.(1,+∞) B.(-∞,1)
C.(-1,+∞) D.(-∞,-1)
【解析】函数f(x)=x2+2(m-1)x-5m-2开口向上,函数f(x)的两个零点x1,x2满足x1<1,x2>1,可得1+2(m-1)-5m-2<0,
解得m>-1.
【答案】C
8.函数f(x)=lg x-的零点所在的区间是( ).
A.(0,1) B.(1,10)
C.(10,100) D.(100,+∞)
【解析】∵f(1)=-1<0,f(10)=1-=>0,
∴f(1)·f(10)<0,由函数零点存在性定理知,函数f(x)=lg x-的零点所在的区间是(1,10),故选B.
【答案】B
9.已知a是函数f(x)的一个零点,且x1
C.f(x1)·f(x2)≥0 D.以上都不对
【解析】定理的逆定理不成立,故f(x1)·f(x2)的值不确定.
【答案】D
10. 二次函数f(x)=ax2+bx+c的部分对应值如下表:
x
-3
-2
-1
0
1
2
3
4
f(x)
6
m
-4
-6
-6
-4
n
6
不求a,b,c的值,判断方程ax2+bx+c=0的两个根所在的区间是( ).
A.(-3,-1)和(2,4) B.(-3,-1)和(-1,1)
C.(-1,1)和(1,2) D.(-∞,-3)和(4,+∞)
【解析】因为f(-3)=6>0,f(-1)=-4<0,所以方程在区间(-3,-1)内必有根.又f(2)=-4<0,f(4)=6>0,所以方程在区间(2,4)内必有根.
【答案】A
11.函数f(x)=|x|+k有两个零点,则( ).
A.k=0 B.k>0 C.0≤k<1 D.k<0
【解析】在同一平面直角坐标系中作出函数y1=|x|和y2=-k的图象,如图所示.若函数f(x)有两个零点,则必有-k>0,即k<0.
【答案】D
12.设函数f(x)在(-∞,+∞)上有意义,对于给定的正数k,定义函数fk(x)=取k=,f(x)=,则fk(x)=的零点有( ).
A.0个 B.1个
C.2个 D.不确定,随k的变化而变化
【解析】取k=,f(x)=,则fk(x)=的图象如图所示.
则fk(x)=的零点就是fk(x)与y==的交点,故交点有两个,即零点有两个.
【答案】C
二、填空题
13.对于函数y=f(x),如果f(x0)=x0,我们就称实数x0是函数f(x)的不动点.设函数f(x)=3+log2x,则函数f(x)的不动点一共有 个.?
【解析】由题意得3+log2x=x,即log2x=x-3,
画出函数y=log2x和y=x-3的图象,如图所示.
结合图象,函数有2个交点,即函数f(x)的不动点一共有2个.
【答案】2
14.若函数f(x)=|2x-2|-b有两个零点,则实数b的取值范围是 .?
【解析】由f(x)=|2x-2|-b=0,得|2x-2|=b.
在同一平面直角坐标系中画出y=|2x-2|与y=b的图象(如图),
则当0
15.已知函数y=lox与y=kx的图象有公共点A,且点A的横坐标为2,则k的值为 .?
【解析】当x=2时,y=lo2=-,
∵点在直线y=kx上,∴k=-.
【答案】-
16.函数f(x)=若关于x的方程f(x)=kx-k至少有两个不相等的实数根,则实数k的取值范围为 .?
【解析】由函数图象(图略)可知,当直线y=kx-k过点时,直线的斜率最小,即k=-;当直线y=kx-k与函数y=x2-x(x>0)相切时有一个交点,k=y'=1,故当函数f(x)与直线y=kx-k有两个不同的交点,即关于x的方程f(x)=kx-k至少有两个不相等的实数根时,则实数k的取值范围是∪(1,+∞).
【答案】∪(1,+∞)
三、解答题
17.若二次函数f(x)=-x2+2ax+4a+1的一个零点小于-1,另一个零点大于3,求实数a的取值范围.
【解析】因为二次函数f(x)=-x2+2ax+4a+1的图象开口向下,且在区间(-∞,-1)内与区间(3,+∞)内各有一个零点,所以
即
即解得a>.
故实数a的取值范围是.
18.已知函数f(x)=lg (a>0)为奇函数,函数g(x)=+b(b∈R).
(1)求a的值;
(2)若b>1,讨论方程g(x)=ln |x|实数根的个数.
【解析】(1)由f(x)=lg(a>0)为奇函数,得f(-x)+f(x)=0,
即lg +lg =lg =0,
所以=1,解得a=1(a=-1舍去).
(2)当b>1时,设h(x)=g(x)-ln |x|=+b-ln |x|,
则h(x)是偶函数且在(0,+∞)上单调递减,
又h(1)=2+b>0,h(e2b)=-b<-1<0,
所以h(x)在(0,+∞)上有唯一的零点,方程g(x)=ln |x|有2个实数根.
19.某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元.该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.
(1)当一次订购量为多少个时,零件的实际出厂单价恰好降为51元?
(2)设一次订购量为x个,零件的实际出厂单价为P元,写出P关于x的函数表达式.
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂单价-成本)
【解析】(1)设每个零件的实际出厂单价恰好降为51元时,一次订购量为x0个,则x0=100+=550.
因此,当一次订购量为550个时,每个零件的实际出厂单价恰好降为51元.
(2)当0
所以P=f(x)=(x∈N).
(3)设销售商的一次订购量为x个时,工厂获得的利润为L元,
则L=(P-40)x=.
当x=500时,L=6000;
当x=1000时,L=11000.
因此,当销售商一次订购500个零件时,该厂获得的利润是6000元;
如果订购1000个,该厂获得的利润是11000元.
20.某公司制定了一个激励销售人员的奖励方案:当销售利润不超过10万元时,按销售利润的15%进行奖励;当销售利润超过10万元时,若超出A万元,则超出部分按2log5(A+1)进行奖励.记奖金为y(单位:万元),销售利润为x(单位:万元).
(1)写出奖金y关于销售利润x的关系式.
(2)如果业务员老江获得5.5万元的奖金,那么他的销售利润是多少万元?
【解析】(1)由题意知,y=
(2)由题意知,1.5+2log5(x-9)=5.5,
2log5(x-9)=4,
log5(x-9)=2,
得x-9=52,
解得x=34.
故业务员老江的销售利润是34万元.
21.某医药研究所开发一种新药,据监测,如果成人按规定的剂量服用,服用药后每毫升血液中的含药量y(微克)与服药的时间t(小时)之间的关系近似满足如图所示的曲线,其中OA是线段,曲线AB是函数y=kat(t≥1,a>0,且k,a是常数)的图象.
(1)写出服药后y关于t的函数关系式.
(2)据监测,每毫升血液中的含药量不少于2微克时治疗疾病有效.假设某人第一次服药为早上6:00,为保持疗效,第二次服药最迟应当在当天几点钟?
(3)若按(2)中的最迟时间服用第二次药,则第二次服药3小时后,该病人每毫升血液中的含药量为多少微克?(精确到0.1)
【解析】(1)当0≤t<1时,y=8t;
当t≥1时,由解得
∴y=
(2)由8×≥2,解得t≤5.∴第一次服药5小时后,即第二次服药最迟应当在当天上午11点钟服药.
(3)第二次服药3小时后,每毫升血液中含第一次所服药的药量为y1=8×=(微克),含第二次服药的药量为y2=8×=4(微克),∴y1+y2=+4≈4.7(微克).
故第二次服药3小时后,该病人每毫升血液中的含药量约为4.7微克.
22.已知函数f(x)=
(1)计算f的值;
(2)写出f(x)的单调区间;
(3)设函数g(x)=f(x)+c,若函数g(x)有三个零点,求实数c的取值范围.
【解析】(1)由已知得f=f(-2)=-2×(-2)2-4×(-2)+1=1.
所以f=f(1)=1+1=2.
(2)当x≤0时,函数f(x)=-2x2-4x+1=-2(x+1)2+3.
由函数的性质可知,f(x)在区间(-∞,-1)内单调递增,在区间[-1,0]内单调递减;
当x>0时,函数f(x)=x+1,显然f(x)在区间(0,+∞)上单调递增.
综上,f(x)的单调递增区间是(-∞,-1)和(0,+∞),单调递减区间是[-1,0].
(3)作出f(x)的图象,如图.
函数g(x)有三个零点,即方程f(x)+c=0有三个不同实根,
又方程f(x)+c=0等价于方程f(x)=-c,
所以当f(x)的图象与直线y=-c有三个交点时,
函数g(x)有三个零点.
数形结合得1<-c<3,即-3
