2018年高中数学第1章立体几何初步1.2.1平面的基本性质课件8苏教版必修2(14张)
文档属性
| 名称 | 2018年高中数学第1章立体几何初步1.2.1平面的基本性质课件8苏教版必修2(14张) |

|
|
| 格式 | zip | ||
| 文件大小 | 984.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 07:30:36 | ||
图片预览






文档简介
课件14张PPT。1.2.1 平面的基本性质(1)复习回顾与情境创设:空间几何体 利用平面几何知识研究立体几何,是立体几何中最基本的数学方法和数学
思想现实生活中哪些事物能够给我们以平面的形象,它们的共同特征主要哪些?
平面图形投影问题:平静的湖面,干净的地面,课桌面,黑板面等
画面会给你留下怎样的印象呢?问题:当我们想象海平面是一平如镜时,它有什么特点?以上问题给了我们“平面”的直观形象,平面是一个不加定义的概念,
具有“平”、“无限延展”、“无厚薄”的特点.很大、很平.1.平面的认识.① 一个平面的面积可以等于100cm2吗?
②通常200页书会比20页书厚一些,那么200个平面
重合在一起时比20个平面重合在一起时厚吗?无限延展(无边界、无面积)没有厚薄之分本节课除了认识平面外,还要解决以下问题:(1)如何表示平面?(2) 空间的点、直线和平面具有怎样的位置关系?(3)如何用数学语言来表述和研究这些位置关系?Ⅰ. 水平放置的平面(通常画成平行四边形) 锐角为45?;
短边长为长边的一半.
Ⅱ.平面的表示:
①用顶点字母表示,如平面ABCD.
②平行四边形也可用对角顶点的字母表示.如平面AC.
③用一个小写希腊字母表示(通常标在锐角),如平面?.
Ⅲ. 两个相交平面
被遮住的部分用虚线表示或不画2.平面的画法及表示.ABCD? 通常我们画出直线的一部分来表示直线;同
样地,我们也可以画出平面的一部分来表示平面.右图中正方体的底面是什么形状?
为何画成了平行四边形?在长方体ABCD—A1B1C1D1中,正方体的三个
面所在平面A1C1,A1B,BC1分别记作?,?,?.
① A1??,B1_____ ?,C1 _____ ?,D1 _____ ?;
② A??,B _____ ?,A1 _____ ?,B1 _____ ?;
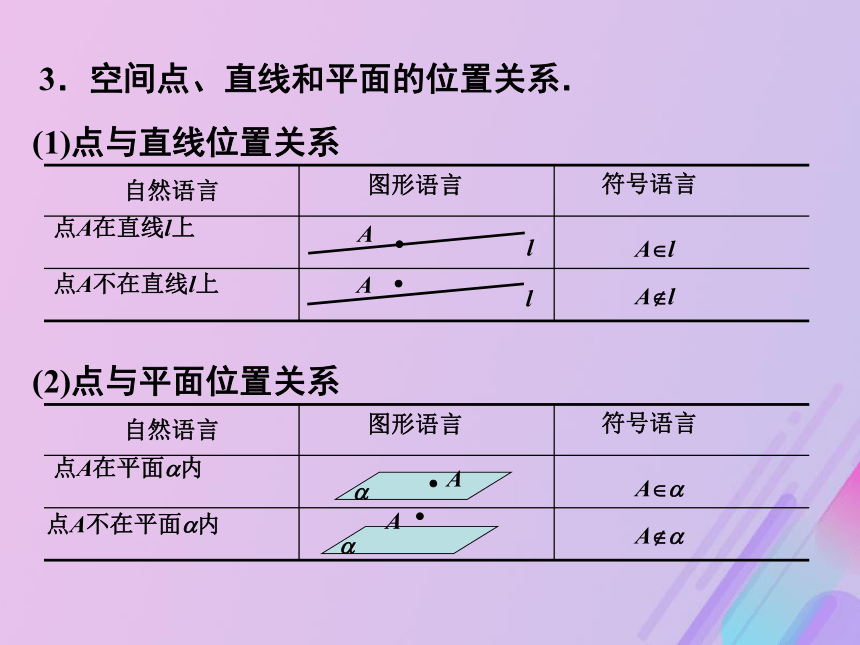
④ ?∩?=A1B1, ?∩?=_____,?∩?=_____.BB1AA1DD1CC1?????? BB1B1C13.空间点、直线和平面的位置关系.(1)点与直线位置关系点A在直线l上A?l点A不在直线l上图形语言符号语言lAlAA?l(2)点与平面位置关系图形语言符号语言点A在平面?内点A不在平面?内A??A??AA??3.空间点、直线和平面的位置关系.3.空间点、直线和平面的位置关系.(3)直线与直线位置关系(平面内)图形语言符号语言l2A(4)直线与平面位置关系符号语言A直线AB在平面?内直线l与平面?交于P点AB∥?直线l1与直线l2相交直线l1与直线l2平行l1l1∩l2=Al2l1l1∥l2直线AB与平面?平行类似地,还有平面与平面的位置关系图形语言P??BA?BAB??l∩?=P 如果一条直线上的两点在一个平面内,那么这
条直线上所有的点都在这个平面内. 4.平面的基本性质.P?Q如图,P??,Q??,则直线PQ与平面?的位置关系为PQ∩?=PA?B公理1:用符号语言可表示为A??B???AB??公理1利用点与平面的位置关系确定直线与平面的位置关系? l??.或表示为A?lB?lA??B??或利用直线与平面的位置关系确定点与平面的位置关系 如果两个平面有一个公共点,那么它们还有其他公共点,这
些公共点的集合是经过此公共点的一条直线 .
符号表示:P??,P?? ? ?∩?=l,P?l .4.平面的基本性质.P??,P??,且?∩?=l ? P?l.公理2常用于:①找两平面的交线;②判定点在线上:即常用于判定三点共线或三线共点.公理2:例1.如图,在长方体ABCD—A1B1C1D1中,P为棱BB1的中点,画出由A1,C1,P三点所确定的平面?与长方体表面的交线. P 因为点P既在平面?内又在平面AB1内,所以点P在平面?与平面AB1的交线上.同理点A1在平面?与平面AB1的交线上.因此,PA1就是平面?与平面AB1的交线 同理,连结PC1,A1C1,它们都是平面?与长方体表面交线的一部分.公理3可表述为:不在同一条直线上的三点,可以确定一个平面.公理3:经过不在同一直线上的三点,有且只有一个平面.有——存在性只有——惟一性例2:已知△ABC在平面?外,它的三边所在直线分别交?于P,Q,R.
求证:P,Q,R三点共线.?三点共线 ? 点在线上PRQ找两个平面的交线:
如图,点P是长方体ABCD-A1B1C1D1的棱AB上一点(不同于端点A,B),试画出由D1,C,P三点所确定的平面?与长方体表面的交线.PQR1.下列叙述中,正确的是_______.
①因为P??,Q??,所以PQ??;
②因为P??,Q??,所以?∩?=PQ;
③因为AB??,C?AB,D?AB,所以CD??;
④因为AB??,AB??,所以?∩?=AB. 2.用符号表示下列语句,并画出图形:
(1) 点A在平面?内,点B在平面?外;
(2)直线l 经过平面?外一点P和平面?内一点Q;
(3) 直线l在平面?内,直线m不在平面?内;
(4) 平面?和?相交于直线AB;
(5) 直线l是平面?和?的交线,直线m在平面?内,l 和m相交于点P.练习:
思想现实生活中哪些事物能够给我们以平面的形象,它们的共同特征主要哪些?
平面图形投影问题:平静的湖面,干净的地面,课桌面,黑板面等
画面会给你留下怎样的印象呢?问题:当我们想象海平面是一平如镜时,它有什么特点?以上问题给了我们“平面”的直观形象,平面是一个不加定义的概念,
具有“平”、“无限延展”、“无厚薄”的特点.很大、很平.1.平面的认识.① 一个平面的面积可以等于100cm2吗?
②通常200页书会比20页书厚一些,那么200个平面
重合在一起时比20个平面重合在一起时厚吗?无限延展(无边界、无面积)没有厚薄之分本节课除了认识平面外,还要解决以下问题:(1)如何表示平面?(2) 空间的点、直线和平面具有怎样的位置关系?(3)如何用数学语言来表述和研究这些位置关系?Ⅰ. 水平放置的平面(通常画成平行四边形) 锐角为45?;
短边长为长边的一半.
Ⅱ.平面的表示:
①用顶点字母表示,如平面ABCD.
②平行四边形也可用对角顶点的字母表示.如平面AC.
③用一个小写希腊字母表示(通常标在锐角),如平面?.
Ⅲ. 两个相交平面
被遮住的部分用虚线表示或不画2.平面的画法及表示.ABCD? 通常我们画出直线的一部分来表示直线;同
样地,我们也可以画出平面的一部分来表示平面.右图中正方体的底面是什么形状?
为何画成了平行四边形?在长方体ABCD—A1B1C1D1中,正方体的三个
面所在平面A1C1,A1B,BC1分别记作?,?,?.
① A1??,B1_____ ?,C1 _____ ?,D1 _____ ?;
② A??,B _____ ?,A1 _____ ?,B1 _____ ?;
④ ?∩?=A1B1, ?∩?=_____,?∩?=_____.BB1AA1DD1CC1?????? BB1B1C13.空间点、直线和平面的位置关系.(1)点与直线位置关系点A在直线l上A?l点A不在直线l上图形语言符号语言lAlAA?l(2)点与平面位置关系图形语言符号语言点A在平面?内点A不在平面?内A??A??AA??3.空间点、直线和平面的位置关系.3.空间点、直线和平面的位置关系.(3)直线与直线位置关系(平面内)图形语言符号语言l2A(4)直线与平面位置关系符号语言A直线AB在平面?内直线l与平面?交于P点AB∥?直线l1与直线l2相交直线l1与直线l2平行l1l1∩l2=Al2l1l1∥l2直线AB与平面?平行类似地,还有平面与平面的位置关系图形语言P??BA?BAB??l∩?=P 如果一条直线上的两点在一个平面内,那么这
条直线上所有的点都在这个平面内. 4.平面的基本性质.P?Q如图,P??,Q??,则直线PQ与平面?的位置关系为PQ∩?=PA?B公理1:用符号语言可表示为A??B???AB??公理1利用点与平面的位置关系确定直线与平面的位置关系? l??.或表示为A?lB?lA??B??或利用直线与平面的位置关系确定点与平面的位置关系 如果两个平面有一个公共点,那么它们还有其他公共点,这
些公共点的集合是经过此公共点的一条直线 .
符号表示:P??,P?? ? ?∩?=l,P?l .4.平面的基本性质.P??,P??,且?∩?=l ? P?l.公理2常用于:①找两平面的交线;②判定点在线上:即常用于判定三点共线或三线共点.公理2:例1.如图,在长方体ABCD—A1B1C1D1中,P为棱BB1的中点,画出由A1,C1,P三点所确定的平面?与长方体表面的交线. P 因为点P既在平面?内又在平面AB1内,所以点P在平面?与平面AB1的交线上.同理点A1在平面?与平面AB1的交线上.因此,PA1就是平面?与平面AB1的交线 同理,连结PC1,A1C1,它们都是平面?与长方体表面交线的一部分.公理3可表述为:不在同一条直线上的三点,可以确定一个平面.公理3:经过不在同一直线上的三点,有且只有一个平面.有——存在性只有——惟一性例2:已知△ABC在平面?外,它的三边所在直线分别交?于P,Q,R.
求证:P,Q,R三点共线.?三点共线 ? 点在线上PRQ找两个平面的交线:
如图,点P是长方体ABCD-A1B1C1D1的棱AB上一点(不同于端点A,B),试画出由D1,C,P三点所确定的平面?与长方体表面的交线.PQR1.下列叙述中,正确的是_______.
①因为P??,Q??,所以PQ??;
②因为P??,Q??,所以?∩?=PQ;
③因为AB??,C?AB,D?AB,所以CD??;
④因为AB??,AB??,所以?∩?=AB. 2.用符号表示下列语句,并画出图形:
(1) 点A在平面?内,点B在平面?外;
(2)直线l 经过平面?外一点P和平面?内一点Q;
(3) 直线l在平面?内,直线m不在平面?内;
(4) 平面?和?相交于直线AB;
(5) 直线l是平面?和?的交线,直线m在平面?内,l 和m相交于点P.练习:
