2018年高中数学第1章立体几何初步1.2.4平面与平面的位置关系课件10苏教版必修2(21张)
文档属性
| 名称 | 2018年高中数学第1章立体几何初步1.2.4平面与平面的位置关系课件10苏教版必修2(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 07:33:06 | ||
图片预览







文档简介
课件21张PPT。两个平面的位置关系
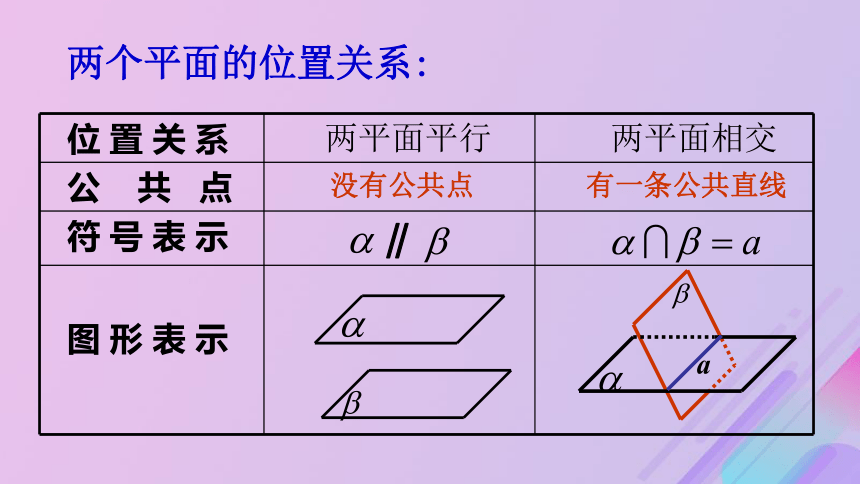
----两平面平行 1. 直线与平面平行的判定定理2. 直线与平面平行的性质定理思考: 空间两个平面可能有哪几种位置关系?温故知新导问题情境:问题1:空间两个平面有哪些位置关系?
问题2:它们公共点的情况是怎样的?
问题3:两个平面没有公共点是什么位置关系?
有公共点是什么位置关系?
导面面平行的定义:
如果两个平面没有公共点,那么就说这两个平面互相平行.两平面相交:
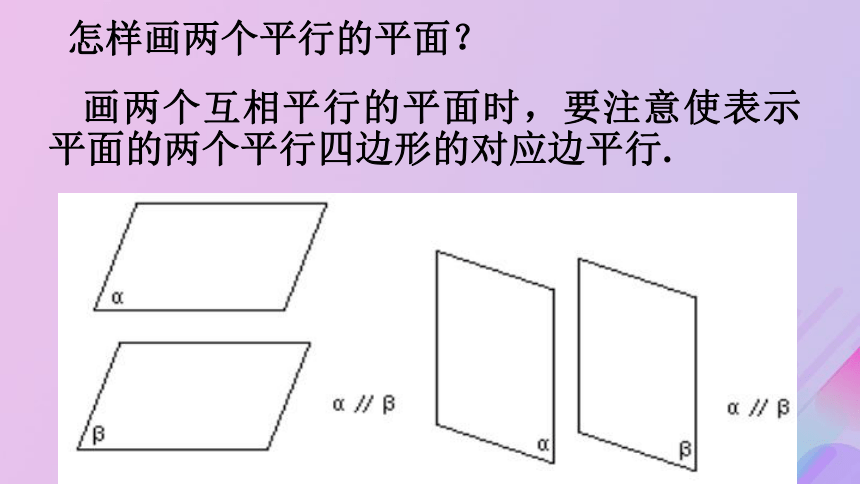
如果两个平面有一个公共点,由公理2可知,那么它们相交于经过这个点的一条直线.此时我们说这两平面相交.建构数学两个平面的位置关系:没有公共点有一条公共直线∥ 画两个互相平行的平面时,要注意使表示平面的两个平行四边形的对应边平行.怎样画两个平行的平面?怎么判断两平面平行?目前判断面面平行只能利用定义.
思有没有更简单的方法?
2.如果一个平面内的两条直线平行于
另一个平面,那么这两个平面是否平行?1. 如果一个平面内的一条直线平行于另一个平面,那么这两个平面是否平行?
探究:议3. 如果一个平面内的两条相交直线都平行
于另一个平面,那么这两个平面是否平行?如何通过线面平行实现面面平行?抽象概括:平面与平面平行的判定定理: 如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.线不在多,贵在相交? //β木工师傅用气泡式水准仪在桌面上交叉放两次,如果水准仪的气泡都是居中的,就可以判定这个桌面和水平面平行,这是什么道理?生活中的应用:用用小试身手:1.判断下列命题是否正确,并说明理由:
(1)若平面?内的两条直线分别与平面?平行,则?与?平行;
(2)若平面?内的无数条直线分别与平面?平行,则?与?平行;
(3)若平面?内的任意一条直线分别与平面?平行,则?与?平行;
2.已知平面α // 平面β,直线 α,求证: // β.D1DCBAC1B1A1例 1: 已知长方体ABCD-A1B1C1D1
求证:平面AB1D1 // 平面C1BD.数学应用:D1DCBAC1B1A1RQP变式:
已知长方体ABCD-A1B1C1D1
(如图), P, Q, R分别为A1A,
A1B1, A1D1 的中点.
求证:平面PQR // 平面C1BD.当堂检测: 1. 判断下列命题是否正确,并说明理由:
(1)若 则 ;
(2)若平面?内的两条相交直线分别与平面?内的两条相交 直线平行,则?与?平行;
(3)平行于同一条直线的两个平面平行;
(4)过已知平面外一条直线,必能作出一个平面与已知平面平行.2.在棱长为a的正方体ABCD-A1B1C1D1中,E,F,G,M,N,Q分别为棱AA1,A1B1,A1D1与BC,CC1,CD的中点.求证:平面EFG∥平面MNQ.本节课学习了
哪些内容?
----两平面平行 1. 直线与平面平行的判定定理2. 直线与平面平行的性质定理思考: 空间两个平面可能有哪几种位置关系?温故知新导问题情境:问题1:空间两个平面有哪些位置关系?
问题2:它们公共点的情况是怎样的?
问题3:两个平面没有公共点是什么位置关系?
有公共点是什么位置关系?
导面面平行的定义:
如果两个平面没有公共点,那么就说这两个平面互相平行.两平面相交:
如果两个平面有一个公共点,由公理2可知,那么它们相交于经过这个点的一条直线.此时我们说这两平面相交.建构数学两个平面的位置关系:没有公共点有一条公共直线∥ 画两个互相平行的平面时,要注意使表示平面的两个平行四边形的对应边平行.怎样画两个平行的平面?怎么判断两平面平行?目前判断面面平行只能利用定义.
思有没有更简单的方法?
2.如果一个平面内的两条直线平行于
另一个平面,那么这两个平面是否平行?1. 如果一个平面内的一条直线平行于另一个平面,那么这两个平面是否平行?
探究:议3. 如果一个平面内的两条相交直线都平行
于另一个平面,那么这两个平面是否平行?如何通过线面平行实现面面平行?抽象概括:平面与平面平行的判定定理: 如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.线不在多,贵在相交? //β木工师傅用气泡式水准仪在桌面上交叉放两次,如果水准仪的气泡都是居中的,就可以判定这个桌面和水平面平行,这是什么道理?生活中的应用:用用小试身手:1.判断下列命题是否正确,并说明理由:
(1)若平面?内的两条直线分别与平面?平行,则?与?平行;
(2)若平面?内的无数条直线分别与平面?平行,则?与?平行;
(3)若平面?内的任意一条直线分别与平面?平行,则?与?平行;
2.已知平面α // 平面β,直线 α,求证: // β.D1DCBAC1B1A1例 1: 已知长方体ABCD-A1B1C1D1
求证:平面AB1D1 // 平面C1BD.数学应用:D1DCBAC1B1A1RQP变式:
已知长方体ABCD-A1B1C1D1
(如图), P, Q, R分别为A1A,
A1B1, A1D1 的中点.
求证:平面PQR // 平面C1BD.当堂检测: 1. 判断下列命题是否正确,并说明理由:
(1)若 则 ;
(2)若平面?内的两条相交直线分别与平面?内的两条相交 直线平行,则?与?平行;
(3)平行于同一条直线的两个平面平行;
(4)过已知平面外一条直线,必能作出一个平面与已知平面平行.2.在棱长为a的正方体ABCD-A1B1C1D1中,E,F,G,M,N,Q分别为棱AA1,A1B1,A1D1与BC,CC1,CD的中点.求证:平面EFG∥平面MNQ.本节课学习了
哪些内容?
