2018年高中数学第2章平面解析几何初步2.1.3两条直线的平行与垂直课件11苏教版必修2(21张)
文档属性
| 名称 | 2018年高中数学第2章平面解析几何初步2.1.3两条直线的平行与垂直课件11苏教版必修2(21张) |  | |
| 格式 | zip | ||
| 文件大小 | 513.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 07:35:34 | ||
图片预览







文档简介
课件21张PPT。3.1.2 两条直线平行与垂直的判定
思考
1.能根据两条直线的斜率判定两条直线是否平行或垂直.
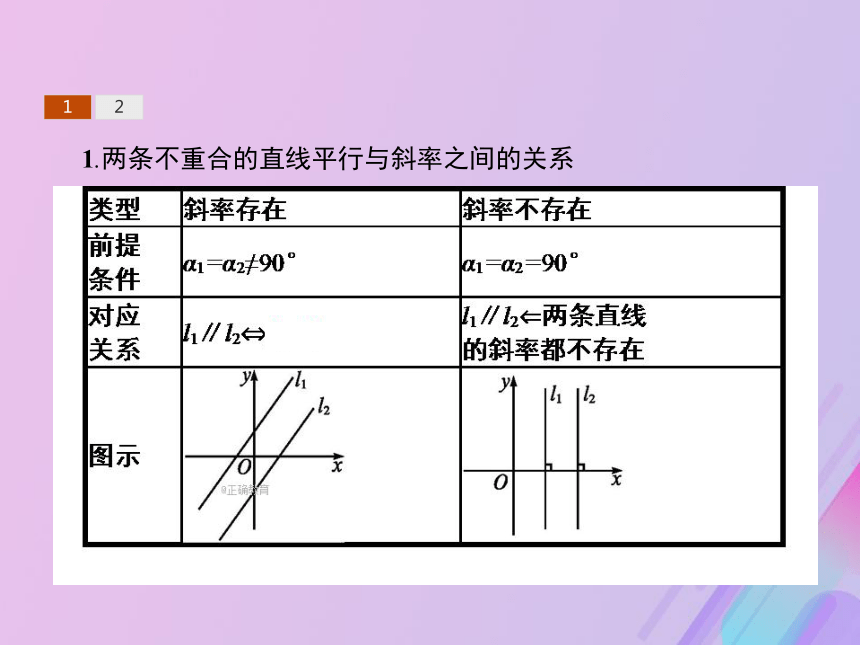
2.能根据两条直线的平行或垂直关系确定两条直线斜率的关系.121.两条不重合的直线平行与斜率之间的关系 12归纳总结1.当直线l1∥直线l2时,可能它们的斜率都存在且相等,也可能斜率都不存在.
2.直线l1,l2的斜率分别为k1,k2,当k1=k2时,l1∥l2或l1与l2重合.
3.对于不重合的直线l1,l2,其倾斜角分别为α,β,有l1∥l2?α=β.L1// L2? k1=k212【做一做1】 已知直线l1∥l2,直线l2的斜率k2=3,则直线l1的斜率k1等于( )
A.可能不存在 B.3
解析:∵l1∥l2,∴k1=k2,
∵k2=3,∴k1=3.
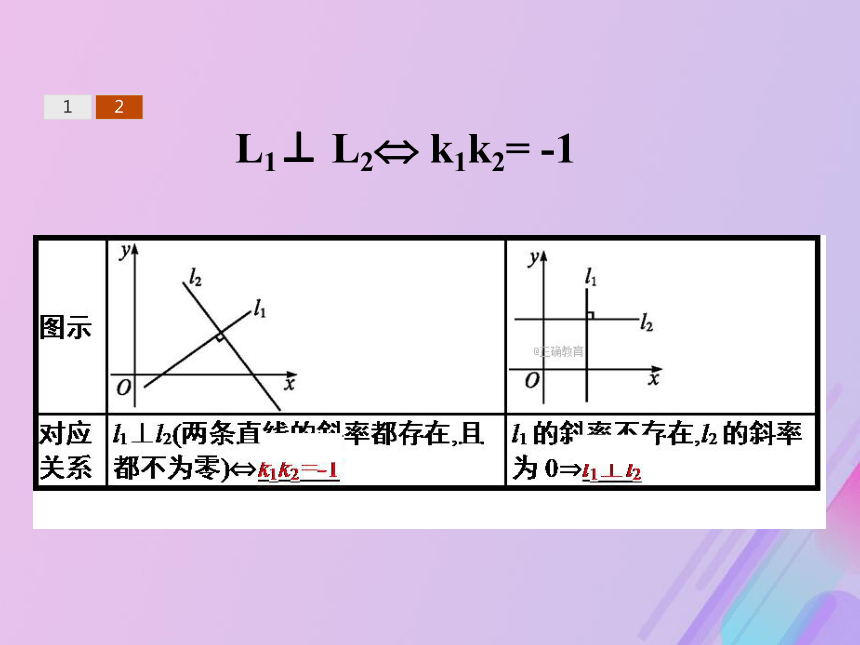
答案:B2.两条直线垂直与斜率之间的关系 12 L1⊥ L2? k1k2= -112题型一题型二题型三题型四【例1】 判断下列各小题中的直线l1与l2是平行还是垂直:
(1)l1经过点A(0,1),B(1,0),l2经过点M(-1,3),N(2,0);
(2)l1经过点A(-1,-2),B(1,2),l2经过点M(-2,-1),N(0,-2);
(3)l1经过点A(1,3),B(1,-4),l2经过点M(2,1),N(2,3);
(4)l1经过点A(3,2),B(3,-1),l2经过点M(1,1),N(2,1).题型一题型二题型一题型二题型一题型二题型一题型二反思判断两条直线l1与l2平行还是垂直时,当它们的斜率都存在时,若k1k2=-1,则l1⊥l2;若k1=k2,再从l1和l2上各取一点P,Q,并计算kPQ,当kPQ≠k1时,l1∥l2,当kPQ=k1=k2时,l1与l2重合;当它们中有一条直线的斜率不存在时,画出图形来判断它们是平行还是垂直.题型一题型二【变式训练1】 顺次连接A(-4,3),B(2,5),C(6,3),D(-3,0)四点所组成的图形是( )
A.平行四边形 B.直角梯形
C.等腰梯形 D.以上都不对题型一题型二【例2】 已知?ABCD的三个顶点分别是A(0,1),B(1,0),C(4,3),求顶点D的坐标.
解:设点D(m,n),由题意得AB∥DC,AD∥BC,
则有kAB=kDC,kAD=kBC,题型一题型二反思解决与平行有关的问题时,常借助于它们的斜率之间的关系来解决,即不重合的两条直线l1与l2平行?k1=k2或k1与k2都不存在.题型一题型二题型一题型二例3 已知直线l1经过点A(3,a),B(a-2,3),直线l2经过点C(2,3),D(-1,a-2),若l1⊥l2,求a的值.
解:由题意知l2的斜率k2一定存在,l1的斜率可能不存在.
当l1的斜率不存在时,3=a-2,即a=5,此时k2=0,
则l1⊥l2,满足题意.
当l1的斜率k1存在时,a≠5,
由斜率公式,得题型一题型二反思解决与垂直有关的问题时,常借助于它们的斜率之间的关系来解决,即l1⊥l2?k1k2=-1或k1与k2中的一个为0,一个不存在.课堂小结
1、L1// L2? k1=k前提:两条直线不重合,斜率都存在) 2
2、L1⊥ L2? k1k2= -1
两条直线都有斜率,
并且都不等于零 作业:同步练习
1.能根据两条直线的斜率判定两条直线是否平行或垂直.
2.能根据两条直线的平行或垂直关系确定两条直线斜率的关系.121.两条不重合的直线平行与斜率之间的关系 12归纳总结1.当直线l1∥直线l2时,可能它们的斜率都存在且相等,也可能斜率都不存在.
2.直线l1,l2的斜率分别为k1,k2,当k1=k2时,l1∥l2或l1与l2重合.
3.对于不重合的直线l1,l2,其倾斜角分别为α,β,有l1∥l2?α=β.L1// L2? k1=k212【做一做1】 已知直线l1∥l2,直线l2的斜率k2=3,则直线l1的斜率k1等于( )
A.可能不存在 B.3
解析:∵l1∥l2,∴k1=k2,
∵k2=3,∴k1=3.
答案:B2.两条直线垂直与斜率之间的关系 12 L1⊥ L2? k1k2= -112题型一题型二题型三题型四【例1】 判断下列各小题中的直线l1与l2是平行还是垂直:
(1)l1经过点A(0,1),B(1,0),l2经过点M(-1,3),N(2,0);
(2)l1经过点A(-1,-2),B(1,2),l2经过点M(-2,-1),N(0,-2);
(3)l1经过点A(1,3),B(1,-4),l2经过点M(2,1),N(2,3);
(4)l1经过点A(3,2),B(3,-1),l2经过点M(1,1),N(2,1).题型一题型二题型一题型二题型一题型二题型一题型二反思判断两条直线l1与l2平行还是垂直时,当它们的斜率都存在时,若k1k2=-1,则l1⊥l2;若k1=k2,再从l1和l2上各取一点P,Q,并计算kPQ,当kPQ≠k1时,l1∥l2,当kPQ=k1=k2时,l1与l2重合;当它们中有一条直线的斜率不存在时,画出图形来判断它们是平行还是垂直.题型一题型二【变式训练1】 顺次连接A(-4,3),B(2,5),C(6,3),D(-3,0)四点所组成的图形是( )
A.平行四边形 B.直角梯形
C.等腰梯形 D.以上都不对题型一题型二【例2】 已知?ABCD的三个顶点分别是A(0,1),B(1,0),C(4,3),求顶点D的坐标.
解:设点D(m,n),由题意得AB∥DC,AD∥BC,
则有kAB=kDC,kAD=kBC,题型一题型二反思解决与平行有关的问题时,常借助于它们的斜率之间的关系来解决,即不重合的两条直线l1与l2平行?k1=k2或k1与k2都不存在.题型一题型二题型一题型二例3 已知直线l1经过点A(3,a),B(a-2,3),直线l2经过点C(2,3),D(-1,a-2),若l1⊥l2,求a的值.
解:由题意知l2的斜率k2一定存在,l1的斜率可能不存在.
当l1的斜率不存在时,3=a-2,即a=5,此时k2=0,
则l1⊥l2,满足题意.
当l1的斜率k1存在时,a≠5,
由斜率公式,得题型一题型二反思解决与垂直有关的问题时,常借助于它们的斜率之间的关系来解决,即l1⊥l2?k1k2=-1或k1与k2中的一个为0,一个不存在.课堂小结
1、L1// L2? k1=k前提:两条直线不重合,斜率都存在) 2
2、L1⊥ L2? k1k2= -1
两条直线都有斜率,
并且都不等于零 作业:同步练习
