2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.1.2椭圆的几何性质课件(25张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.1.2椭圆的几何性质课件(25张) |  | |
| 格式 | zip | ||
| 文件大小 | 636.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 07:44:34 | ||
图片预览




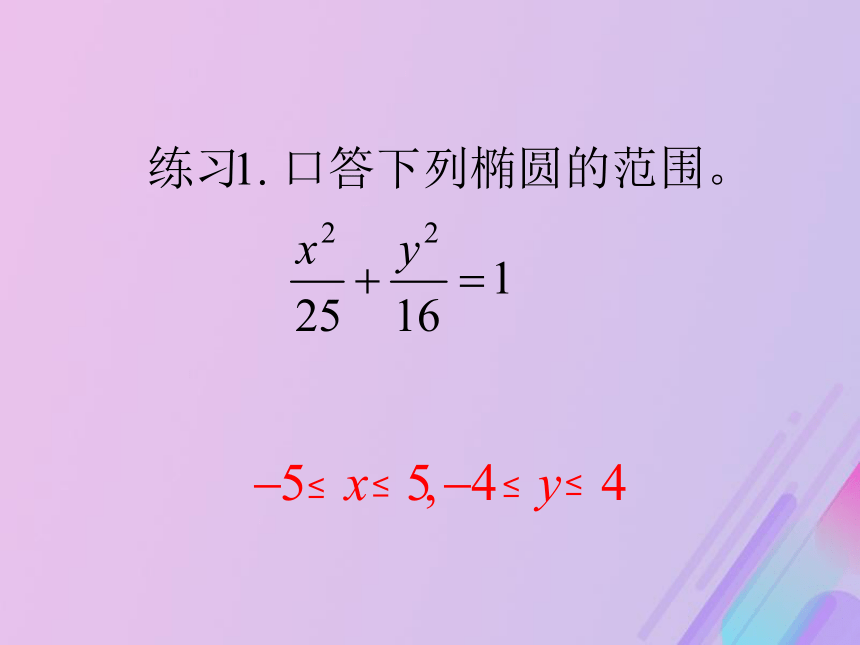



文档简介
课件25张PPT。2.1.2 椭圆的简单几何性质复习:1.椭圆的定义:到两定点F1、F2的距离之和为常数(大于|F1F2 |)的动点的轨迹叫做椭圆。2.椭圆的标准方程是:3.椭圆中a,b,c的关系是:a2=b2+c2当焦点在X轴上时当焦点在Y轴上时 -a≤x≤a, -b≤y≤b 知
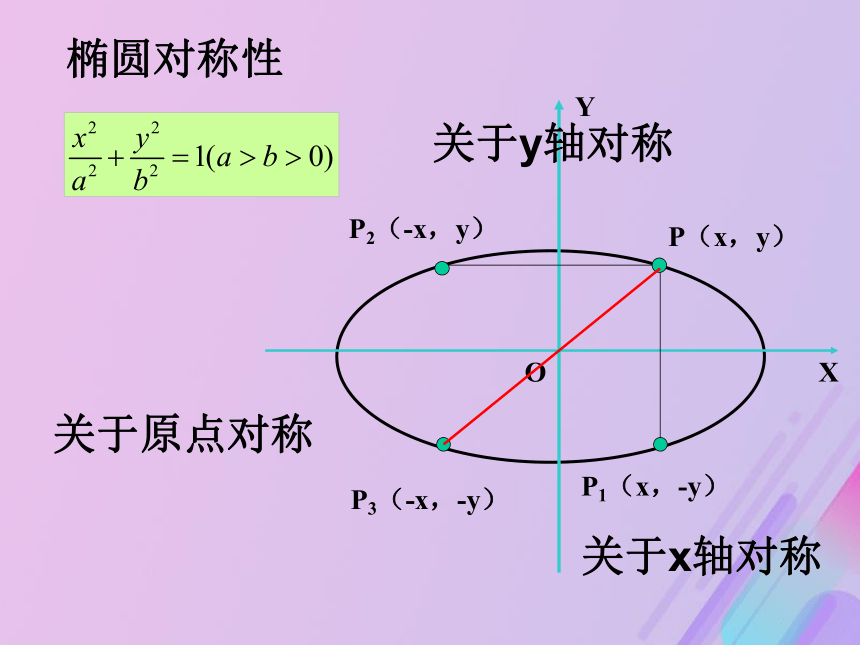
椭圆落在x=±a,y= ± b组成的矩形中一、范围: 关于x轴对称关于y轴对称关于原点对称椭圆对称性二、椭圆的对称性 把(X)换成(-X),方程不变,说明椭圆关于( )轴对称;
把(Y)换成(-Y),方程不变,说明椭圆关于( )轴对称;
把(X)换成(-X), (Y)换成(-Y),方程还是不变,说明椭圆关于( )对称;中心:椭圆的对称中心叫做椭圆的中心。 所以,坐标轴是椭圆的对称轴,原点是椭圆的对称中心。Y X 原点 练习2.三、椭圆的顶点令 x=0,得 y=?,说明椭圆与 y轴的交点( ),
令 y=0,得 x=?, 说明椭圆与 x轴的交点( )*顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。0, ±b±a, 0*长轴、短轴: 线段A1A2、B1B2分别叫做椭圆的长轴和短轴。a、b分别叫做椭圆的长半轴长和短半轴长。练习3练习4. 画出下列椭圆的草图(1)(2)问题2:圆的形状都是相同的,而椭圆却有些比较“扁”,有些比较“圆”,用什么样的量来刻画椭圆“扁”的程度呢?四、椭圆的离心率离心率:椭圆的焦距与长轴长的比:叫做椭圆的离心率。[1]离心率的取值范围:[2]离心率对椭圆形状的影响:02)e 越接近 0,c 就越接近 0,从而 b就越大,椭圆就越圆[3]e与a,b的关系:练习5小结一:基本元素{1}基本量:a、b、c、e、(共四个量){2}基本点:顶点、焦点、中心(共七个点){3}基本线:对称轴(共两条线)请考虑:基本量之间、基本点之间、基本线之间以及它们相互之间的关系(位置、数量之间的关系)|MF1|+|MF2|=2a (2a>|F1F2|)(c,0)、(?c,0)(0,c)、(0,?c)(?a,0)、(0,?b)|x|? a |y|? b|x|? b |y|? a关于x轴、y轴、原点对称(?b,0)、(0,?a)小结二:一个框,四个点,注意光滑和圆扁,莫忘对称要体现 练习6.已知椭圆方程为 则它的长轴长是: ;
短轴长是: ;
焦距是: ;
离心率等于: ;
焦点坐标是: ___;
顶点坐标是: _______;
外切矩形的面积等于: 。 2 例1 求椭圆 16 x2 + 25y2 =400的长轴和短轴的长、离心率、焦点和顶点坐标。解:把已知方程化成标准方程椭圆的长轴长是:离心率:焦点坐标是:四个顶点坐标是:椭圆的短轴长是:2a=102b=8思考1:分析:题目没有指出焦点的位置,要考虑两种位置 小结:1.知识小结:
(1) 学习了椭圆的范围、对称性、顶点坐标、离心率等概念及其几何意义。
(2) 研究了椭圆的几个基本量a,b,c,e及顶点、焦点、对称中心及其相互之间的关系
2.数学思想方法:
(1)数与形的结合,用代数的方法解决几何问题。
(2)分类讨论的数学思想
椭圆落在x=±a,y= ± b组成的矩形中一、范围: 关于x轴对称关于y轴对称关于原点对称椭圆对称性二、椭圆的对称性 把(X)换成(-X),方程不变,说明椭圆关于( )轴对称;
把(Y)换成(-Y),方程不变,说明椭圆关于( )轴对称;
把(X)换成(-X), (Y)换成(-Y),方程还是不变,说明椭圆关于( )对称;中心:椭圆的对称中心叫做椭圆的中心。 所以,坐标轴是椭圆的对称轴,原点是椭圆的对称中心。Y X 原点 练习2.三、椭圆的顶点令 x=0,得 y=?,说明椭圆与 y轴的交点( ),
令 y=0,得 x=?, 说明椭圆与 x轴的交点( )*顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。0, ±b±a, 0*长轴、短轴: 线段A1A2、B1B2分别叫做椭圆的长轴和短轴。a、b分别叫做椭圆的长半轴长和短半轴长。练习3练习4. 画出下列椭圆的草图(1)(2)问题2:圆的形状都是相同的,而椭圆却有些比较“扁”,有些比较“圆”,用什么样的量来刻画椭圆“扁”的程度呢?四、椭圆的离心率离心率:椭圆的焦距与长轴长的比:叫做椭圆的离心率。[1]离心率的取值范围:[2]离心率对椭圆形状的影响:0
短轴长是: ;
焦距是: ;
离心率等于: ;
焦点坐标是: ___;
顶点坐标是: _______;
外切矩形的面积等于: 。 2 例1 求椭圆 16 x2 + 25y2 =400的长轴和短轴的长、离心率、焦点和顶点坐标。解:把已知方程化成标准方程椭圆的长轴长是:离心率:焦点坐标是:四个顶点坐标是:椭圆的短轴长是:2a=102b=8思考1:分析:题目没有指出焦点的位置,要考虑两种位置 小结:1.知识小结:
(1) 学习了椭圆的范围、对称性、顶点坐标、离心率等概念及其几何意义。
(2) 研究了椭圆的几个基本量a,b,c,e及顶点、焦点、对称中心及其相互之间的关系
2.数学思想方法:
(1)数与形的结合,用代数的方法解决几何问题。
(2)分类讨论的数学思想
