2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.3.1抛物线级其标准方程课件(16张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.3.1抛物线级其标准方程课件(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 07:45:50 | ||
图片预览



文档简介
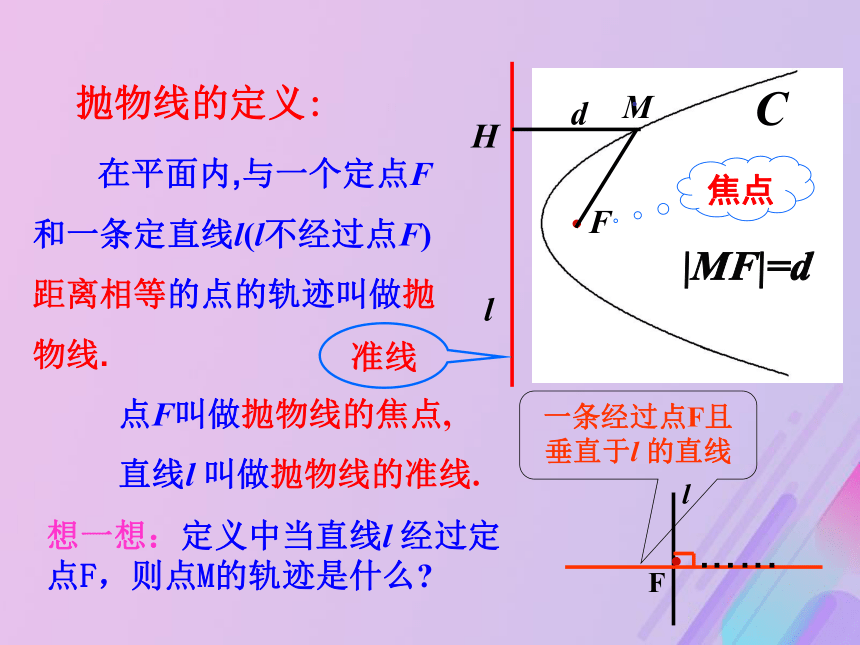
课件16张PPT。2.3.1 抛物线的定义及其标准方程 一条经过点F且垂直于l 的直线抛物线的定义: 在平面内,与一个定点F和一条定直线l(l不经过点F) 距离相等的点的轨迹叫做抛物线.|MF|=d焦点d准线点F叫做抛物线的焦点,
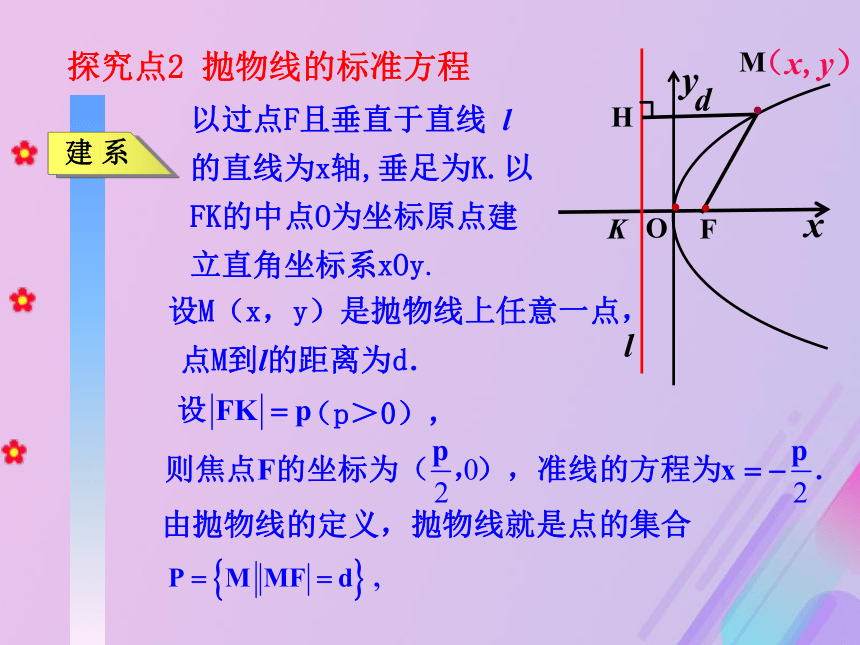
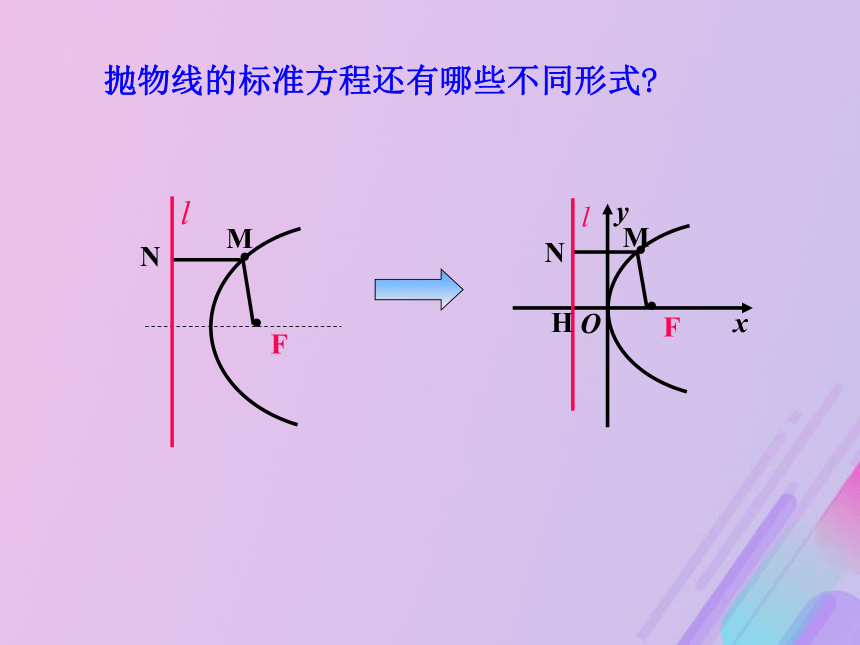
直线l 叫做抛物线的准线.想一想:定义中当直线l 经过定点F,则点M的轨迹是什么?······以过点F且垂直于直线 l 的直线为x轴,垂足为K.以FK的中点O为坐标原点建立直角坐标系xOy.KOFMl···(x,y)设M(x,y)是抛物线上任意一点,H点M到l的距离为d.d由抛物线的定义,抛物线就是点的集合探究点2 抛物线的标准方程两边平方,整理得KOFMl···(x, y)Hd其中p为正常数,它的几何意义是: 焦点到准线的距离.方程 y2 = 2px(p>0)表示焦点在x轴正半轴上的抛物线.抛物线的标准方程还有哪些不同形式?O准线方程焦点坐标标准方程焦点位置 图
形 四种抛物线及其它们的标准方程 x轴的
正半轴上 x轴的
负半轴上 y轴的
正半轴上 y轴的
负半轴上y2=2px(p>0)y2=-2px (p>0)x2=2py (p>0)x2=-2py (p>0)....(1)若一次项的变量为X(或Y),则焦点就在X轴(或Y轴)上; 如何判断抛物线的焦点位置,开口方向?(2)一次项的系数的正负决定了开口方向 即:焦点与一次项变量有关;正负决定开口方向! 【提升总结】【例1】(1)已知抛物线的标准方程是y2=6x,求它的焦点坐标和准线方程.
(2)已知抛物线的焦点是F(0,-2),求它的标准方程.解:(1)因为p=3,故抛物线的焦点坐标为 ,
准线方程为(2)因为抛物线的焦点在y轴的负半轴上,且 故所求抛物线的标准方程为x2=-8y.1.根据下列条件写出抛物线的标准方程.
(1)焦点是(0,-3);
(2)准线是 .
2.求下列抛物线的焦点坐标与准线方程.
(1)y=8x2;
(2)x2+8y=0.x2=-12yy2=2x【提升总结】(1)用待定系数法求抛物线标准方程,应
先确定抛物线的形式,再求p值.(2)求抛物线的
焦点坐标和准线方程要先化成抛物线的标准方程.【变式练习】2、设抛物线y2=8x上一点P到y轴的距离是4,则
点P到该抛物线焦点的距离是( )
A.12 B.4 C.6 D.8 C1、若抛物线 上一点P到其焦点的距离为3,则点P的横坐标等于( ) 23.已知动圆M 经过点A(3,0),且与直线l:x=-3相切,求动圆圆心M的轨迹方程.解析:设动点M(x,y),
设圆M与直线l:x=-3的切点为N,
则|MA|=|MN|,即动点M到定点A和定直线l:x=-3
的距离相等,
所以点M的轨迹是抛物线,
且以A(3,0)为焦点,以直线l:x=-3为准线,
所以 =3,所以p=6.
所以圆心M的轨迹方程是y2=12x.平面内与一个定点F的距离和一条定直线l (l不经过点F)的距离相等的点的轨迹叫做抛物线.一个定义:两类问题:三项注意:四种形式:1.求抛物线标准方程;
2.已知方程求焦点坐标和准线方程.1.定义的前提条件:直线l不经过点F;
2.p的几何意义:焦点到准线的距离;
3.标准方程表示的是顶点在原点,对称轴为坐标轴的抛物线.抛物线的标准方程有四种:
y2=2px(p>0),y2=-2px(p>0),
x2=2py(p>0),x2=-2py(p>0). 追赶时间的人,生活就会宠爱他;放弃时间的人,生活就会冷落他.
直线l 叫做抛物线的准线.想一想:定义中当直线l 经过定点F,则点M的轨迹是什么?······以过点F且垂直于直线 l 的直线为x轴,垂足为K.以FK的中点O为坐标原点建立直角坐标系xOy.KOFMl···(x,y)设M(x,y)是抛物线上任意一点,H点M到l的距离为d.d由抛物线的定义,抛物线就是点的集合探究点2 抛物线的标准方程两边平方,整理得KOFMl···(x, y)Hd其中p为正常数,它的几何意义是: 焦点到准线的距离.方程 y2 = 2px(p>0)表示焦点在x轴正半轴上的抛物线.抛物线的标准方程还有哪些不同形式?O准线方程焦点坐标标准方程焦点位置 图
形 四种抛物线及其它们的标准方程 x轴的
正半轴上 x轴的
负半轴上 y轴的
正半轴上 y轴的
负半轴上y2=2px(p>0)y2=-2px (p>0)x2=2py (p>0)x2=-2py (p>0)....(1)若一次项的变量为X(或Y),则焦点就在X轴(或Y轴)上; 如何判断抛物线的焦点位置,开口方向?(2)一次项的系数的正负决定了开口方向 即:焦点与一次项变量有关;正负决定开口方向! 【提升总结】【例1】(1)已知抛物线的标准方程是y2=6x,求它的焦点坐标和准线方程.
(2)已知抛物线的焦点是F(0,-2),求它的标准方程.解:(1)因为p=3,故抛物线的焦点坐标为 ,
准线方程为(2)因为抛物线的焦点在y轴的负半轴上,且 故所求抛物线的标准方程为x2=-8y.1.根据下列条件写出抛物线的标准方程.
(1)焦点是(0,-3);
(2)准线是 .
2.求下列抛物线的焦点坐标与准线方程.
(1)y=8x2;
(2)x2+8y=0.x2=-12yy2=2x【提升总结】(1)用待定系数法求抛物线标准方程,应
先确定抛物线的形式,再求p值.(2)求抛物线的
焦点坐标和准线方程要先化成抛物线的标准方程.【变式练习】2、设抛物线y2=8x上一点P到y轴的距离是4,则
点P到该抛物线焦点的距离是( )
A.12 B.4 C.6 D.8 C1、若抛物线 上一点P到其焦点的距离为3,则点P的横坐标等于( ) 23.已知动圆M 经过点A(3,0),且与直线l:x=-3相切,求动圆圆心M的轨迹方程.解析:设动点M(x,y),
设圆M与直线l:x=-3的切点为N,
则|MA|=|MN|,即动点M到定点A和定直线l:x=-3
的距离相等,
所以点M的轨迹是抛物线,
且以A(3,0)为焦点,以直线l:x=-3为准线,
所以 =3,所以p=6.
所以圆心M的轨迹方程是y2=12x.平面内与一个定点F的距离和一条定直线l (l不经过点F)的距离相等的点的轨迹叫做抛物线.一个定义:两类问题:三项注意:四种形式:1.求抛物线标准方程;
2.已知方程求焦点坐标和准线方程.1.定义的前提条件:直线l不经过点F;
2.p的几何意义:焦点到准线的距离;
3.标准方程表示的是顶点在原点,对称轴为坐标轴的抛物线.抛物线的标准方程有四种:
y2=2px(p>0),y2=-2px(p>0),
x2=2py(p>0),x2=-2py(p>0). 追赶时间的人,生活就会宠爱他;放弃时间的人,生活就会冷落他.
