2018年高中数学第二章圆锥曲线与方程2.1.1曲线与方程的概念课件3新人教B版选修2_1(14张)
文档属性
| 名称 | 2018年高中数学第二章圆锥曲线与方程2.1.1曲线与方程的概念课件3新人教B版选修2_1(14张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 00:00:00 | ||
图片预览





文档简介
课件14张PPT。第二章
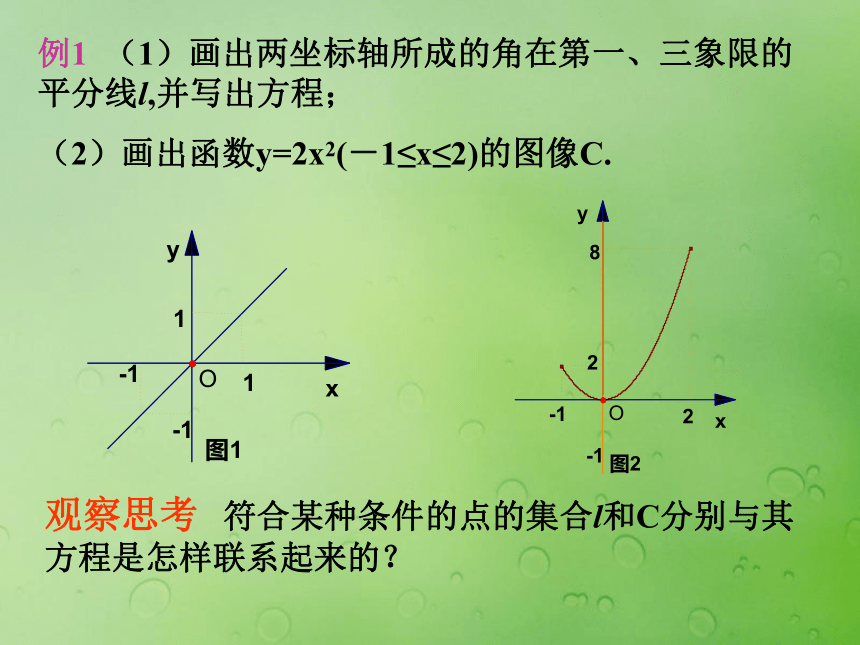
圆锥曲线与方程 用垂直于圆锥的轴平面截圆锥,截口曲线是——圆,改变平面与圆锥轴线的夹角得到的图形是什么? 圆、椭圆、双曲线、抛物线统称为圆锥曲线. 行星绕太阳运行轨道是椭圆;探照灯反射镜面是抛物线绕对称轴旋转形成抛物面;发电厂冷却塔外形是双曲线.曲线与方程 解析几何重要内容之一是利用代数方法来研究几何中曲线问题.即通过建立坐标系,利用平面内点和有序数对之间一一对应关系,建立曲线方程,并通过对方程的讨论来研究曲线的几何性质——用坐标法研究几何图形是解析几何思想的精髓. 圆锥曲线发现与研究始于古希腊.当时人们从纯几何学观点研究这种与圆密切相关的曲线,它们的几何性质是圆的几何性质推广.17世纪初期,笛卡儿发明了坐标系,开始用代数方法研究圆锥曲线.例1 (1)画出两坐标轴所成的角在第一、三象限的平分线l,并写出方程;
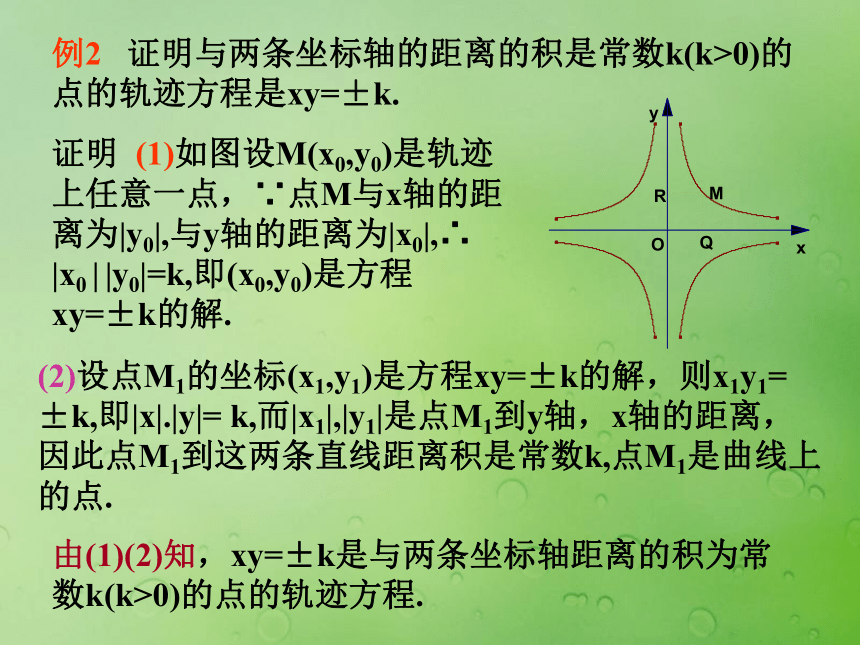
(2)画出函数y=2x2(-1≤x≤2)的图像C.观察思考 符合某种条件的点的集合l和C分别与其方程是怎样联系起来的?“曲线的方程”与“方程的曲线(图形)”定义: 一般地,在直角坐标系中,如果某曲线C上的点与一个二元方程f(x,y)=0的解建立如下关系:1.曲线上的点的坐标都是这个方程的解;2.以这个方程的解为坐标的点都在曲线上,那么这个方程叫做曲线的方程,这条曲线叫方程的曲线.练习 举3个例子,每个例子画一条曲线,写一个方程.第一个例子满足定义中两个条件;第二个例子满足定义中(1),不满足(2);第三个例子满足定义中的(2)不满足(1).例2 证明与两条坐标轴的距离的积是常数k(k>0)的点的轨迹方程是xy=±k.证明 (1)如图设M(x0,y0)是轨迹上任意一点,∵点M与x轴的距离为|y0|,与y轴的距离为|x0|,∴ |x0 | |y0|=k,即(x0,y0)是方程xy=±k的解.(2)设点M1的坐标(x1,y1)是方程xy=±k的解,则x1y1= ±k,即|x|.|y|= k,而|x1|,|y1|是点M1到y轴,x轴的距离,因此点M1到这两条直线距离积是常数k,点M1是曲线上的点.由(1)(2)知,xy=±k是与两条坐标轴距离的积为常数k(k>0)的点的轨迹方程.归纳 证明已知曲线C的方程是f(x,y)=0方法和步骤:
(1)设M(x0,y0)是曲线C上任一点,证明(x0,y0)是f(x,y)=0的解;(2)设(x0,y0)是f(x,y)=0的解,证明点M(x0,y0)在曲线C上. 最后不要忘了归纳总结例2 求曲线y=x2关于直线y=x的对称图形的方程.例3 求曲线y=x3-x关于点(1,2)的对称曲线的方程.求曲线方程步骤
(1)建立适当坐标系,设点M的坐标(x,y)
(2)写出适合条件P的点M的集合P={M|p(M)}
(3)用坐标表示条件p(M),列出方程f(x,y)=0
(4)化方程f(x,y)=0为最简形式
(5)说明化简后的方程的解为坐标的点都在曲线上.
注 化简前后方程解集是相同的,(5)可以省略不写,如有特殊情况,适当说明.归纳 证明已知曲线C的方程是f(x,y)=0方法和步骤:
(1)设M(x0,y0)是曲线C上任一点,证明(x0,y0)是f(x,y)=0的解;
(2)设(x0,y0)是f(x,y)=0的解,证明点M(x0,y0)在曲线C上.
最后不要忘了归纳总结练习:
1.如果曲线C上的点满足方程F(x,y)=0,则以下说法正确的是( )
A.曲线C 的方程是F(x,y)=0
B.方程F(x,y)=0的曲线是C
C.坐标满足方程F(x,y)=0的点在曲线C上
D.坐标不满足方程F(x,y)=0的点不在曲线C上2.判断下列结论的正误,并说明理由.
(1)过点A(3,0)且垂直于y 轴的直线的方程为y=0;
(2)到x轴距离为2的点的直线方程为y=-2;
(3)△ABC的顶点A(0,-3),B(1,0),C(-1,0)
D为BC中点,则中线AD的方程为x=0 D???3.方程(3x-4y-12)·[log2(x+2y)-3]=0 的曲线经过点A(0,-3)、B(0,4)、
C( )、D(4,0)中的( )
A.0个 B.1个 C.2个 D.3个 4.如果两条曲线的方程F1(x,y)=0和F2(x,y)=0,它们的交点M(x0,y0),
求证:方程F1(x,y)+λF2(x,y)=0表示的曲线也经过M点.(λ为任意常数)分析:只要将M点的坐标代入方程.
F1(x,y)+λF2(x,y)=0,看点M的坐标是否满足方程即可B 小结:
1.“曲线的方程”、“方程的曲线”的定义.
牢记关系(1)、(2)两者缺一不可,它们都是“曲线的方程”和“方程的曲线”的必要条件.两者满足了,“曲线的方程”和“方程的曲线”才具备充分性.
2.曲线的研究转化为方程来研究,即几何问题的研究转化为代数问题.这种“以数论形”的思想是解析几何的基本思想和基本方法
作业:P40习题2.1 第1、2题 例3 设A,B两点的坐标分别是(-1,-1),(3,7),求线段AB的垂直平分线的方程.解 (1)设点M(x,y)是线段AB的垂直平分线上任一点,即(2)点M属于集合P={M||MA|=|MB|}.(3)点M适合条件用坐标表示为:(4)上式两边平方整理得x+2y-7=0. ①(5)下面证明方程①是线段AB的垂直平分线的方程.思考 如何证明方程①是线段AB的垂直平分线的方程?思考 如何根据已知条件求出表示曲线的方程?例4 已知一条直线l和它上方的一个点F,点F到l的距离是2,一条曲线也在l的上方,它上面的每一点到F的距离减去到l的距离的差都是2,建立适当坐标系,求这条曲线得方程.分析 如何建立坐标系?解 取直线l为x轴,过点F且垂直于直线l的直线为y轴,建立坐标系xOy.设点M(x,y)是曲线上任意一点,作MB⊥x轴,垂足为B,则点M属于集合P={M||MF|-|MB|=2}.两边平方得x2+(y-2)2=(y+2)2,即y=(1/8)x2.∵曲线在x轴上方,∴y>0.故所求曲线方程是
圆锥曲线与方程 用垂直于圆锥的轴平面截圆锥,截口曲线是——圆,改变平面与圆锥轴线的夹角得到的图形是什么? 圆、椭圆、双曲线、抛物线统称为圆锥曲线. 行星绕太阳运行轨道是椭圆;探照灯反射镜面是抛物线绕对称轴旋转形成抛物面;发电厂冷却塔外形是双曲线.曲线与方程 解析几何重要内容之一是利用代数方法来研究几何中曲线问题.即通过建立坐标系,利用平面内点和有序数对之间一一对应关系,建立曲线方程,并通过对方程的讨论来研究曲线的几何性质——用坐标法研究几何图形是解析几何思想的精髓. 圆锥曲线发现与研究始于古希腊.当时人们从纯几何学观点研究这种与圆密切相关的曲线,它们的几何性质是圆的几何性质推广.17世纪初期,笛卡儿发明了坐标系,开始用代数方法研究圆锥曲线.例1 (1)画出两坐标轴所成的角在第一、三象限的平分线l,并写出方程;
(2)画出函数y=2x2(-1≤x≤2)的图像C.观察思考 符合某种条件的点的集合l和C分别与其方程是怎样联系起来的?“曲线的方程”与“方程的曲线(图形)”定义: 一般地,在直角坐标系中,如果某曲线C上的点与一个二元方程f(x,y)=0的解建立如下关系:1.曲线上的点的坐标都是这个方程的解;2.以这个方程的解为坐标的点都在曲线上,那么这个方程叫做曲线的方程,这条曲线叫方程的曲线.练习 举3个例子,每个例子画一条曲线,写一个方程.第一个例子满足定义中两个条件;第二个例子满足定义中(1),不满足(2);第三个例子满足定义中的(2)不满足(1).例2 证明与两条坐标轴的距离的积是常数k(k>0)的点的轨迹方程是xy=±k.证明 (1)如图设M(x0,y0)是轨迹上任意一点,∵点M与x轴的距离为|y0|,与y轴的距离为|x0|,∴ |x0 | |y0|=k,即(x0,y0)是方程xy=±k的解.(2)设点M1的坐标(x1,y1)是方程xy=±k的解,则x1y1= ±k,即|x|.|y|= k,而|x1|,|y1|是点M1到y轴,x轴的距离,因此点M1到这两条直线距离积是常数k,点M1是曲线上的点.由(1)(2)知,xy=±k是与两条坐标轴距离的积为常数k(k>0)的点的轨迹方程.归纳 证明已知曲线C的方程是f(x,y)=0方法和步骤:
(1)设M(x0,y0)是曲线C上任一点,证明(x0,y0)是f(x,y)=0的解;(2)设(x0,y0)是f(x,y)=0的解,证明点M(x0,y0)在曲线C上. 最后不要忘了归纳总结例2 求曲线y=x2关于直线y=x的对称图形的方程.例3 求曲线y=x3-x关于点(1,2)的对称曲线的方程.求曲线方程步骤
(1)建立适当坐标系,设点M的坐标(x,y)
(2)写出适合条件P的点M的集合P={M|p(M)}
(3)用坐标表示条件p(M),列出方程f(x,y)=0
(4)化方程f(x,y)=0为最简形式
(5)说明化简后的方程的解为坐标的点都在曲线上.
注 化简前后方程解集是相同的,(5)可以省略不写,如有特殊情况,适当说明.归纳 证明已知曲线C的方程是f(x,y)=0方法和步骤:
(1)设M(x0,y0)是曲线C上任一点,证明(x0,y0)是f(x,y)=0的解;
(2)设(x0,y0)是f(x,y)=0的解,证明点M(x0,y0)在曲线C上.
最后不要忘了归纳总结练习:
1.如果曲线C上的点满足方程F(x,y)=0,则以下说法正确的是( )
A.曲线C 的方程是F(x,y)=0
B.方程F(x,y)=0的曲线是C
C.坐标满足方程F(x,y)=0的点在曲线C上
D.坐标不满足方程F(x,y)=0的点不在曲线C上2.判断下列结论的正误,并说明理由.
(1)过点A(3,0)且垂直于y 轴的直线的方程为y=0;
(2)到x轴距离为2的点的直线方程为y=-2;
(3)△ABC的顶点A(0,-3),B(1,0),C(-1,0)
D为BC中点,则中线AD的方程为x=0 D???3.方程(3x-4y-12)·[log2(x+2y)-3]=0 的曲线经过点A(0,-3)、B(0,4)、
C( )、D(4,0)中的( )
A.0个 B.1个 C.2个 D.3个 4.如果两条曲线的方程F1(x,y)=0和F2(x,y)=0,它们的交点M(x0,y0),
求证:方程F1(x,y)+λF2(x,y)=0表示的曲线也经过M点.(λ为任意常数)分析:只要将M点的坐标代入方程.
F1(x,y)+λF2(x,y)=0,看点M的坐标是否满足方程即可B 小结:
1.“曲线的方程”、“方程的曲线”的定义.
牢记关系(1)、(2)两者缺一不可,它们都是“曲线的方程”和“方程的曲线”的必要条件.两者满足了,“曲线的方程”和“方程的曲线”才具备充分性.
2.曲线的研究转化为方程来研究,即几何问题的研究转化为代数问题.这种“以数论形”的思想是解析几何的基本思想和基本方法
作业:P40习题2.1 第1、2题 例3 设A,B两点的坐标分别是(-1,-1),(3,7),求线段AB的垂直平分线的方程.解 (1)设点M(x,y)是线段AB的垂直平分线上任一点,即(2)点M属于集合P={M||MA|=|MB|}.(3)点M适合条件用坐标表示为:(4)上式两边平方整理得x+2y-7=0. ①(5)下面证明方程①是线段AB的垂直平分线的方程.思考 如何证明方程①是线段AB的垂直平分线的方程?思考 如何根据已知条件求出表示曲线的方程?例4 已知一条直线l和它上方的一个点F,点F到l的距离是2,一条曲线也在l的上方,它上面的每一点到F的距离减去到l的距离的差都是2,建立适当坐标系,求这条曲线得方程.分析 如何建立坐标系?解 取直线l为x轴,过点F且垂直于直线l的直线为y轴,建立坐标系xOy.设点M(x,y)是曲线上任意一点,作MB⊥x轴,垂足为B,则点M属于集合P={M||MF|-|MB|=2}.两边平方得x2+(y-2)2=(y+2)2,即y=(1/8)x2.∵曲线在x轴上方,∴y>0.故所求曲线方程是
