2018年高中数学第二章圆锥曲线与方程2.2.2椭圆的几何性质课件4新人教B版选修2_1(16张)
文档属性
| 名称 | 2018年高中数学第二章圆锥曲线与方程2.2.2椭圆的几何性质课件4新人教B版选修2_1(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 00:00:00 | ||
图片预览





文档简介
课件16张PPT。2.2.2 椭圆的几何性质
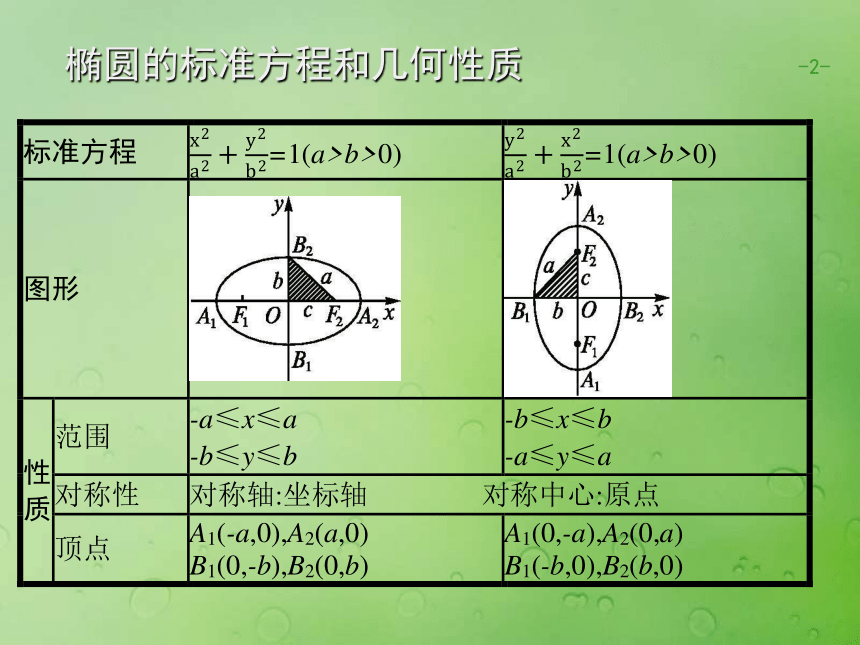
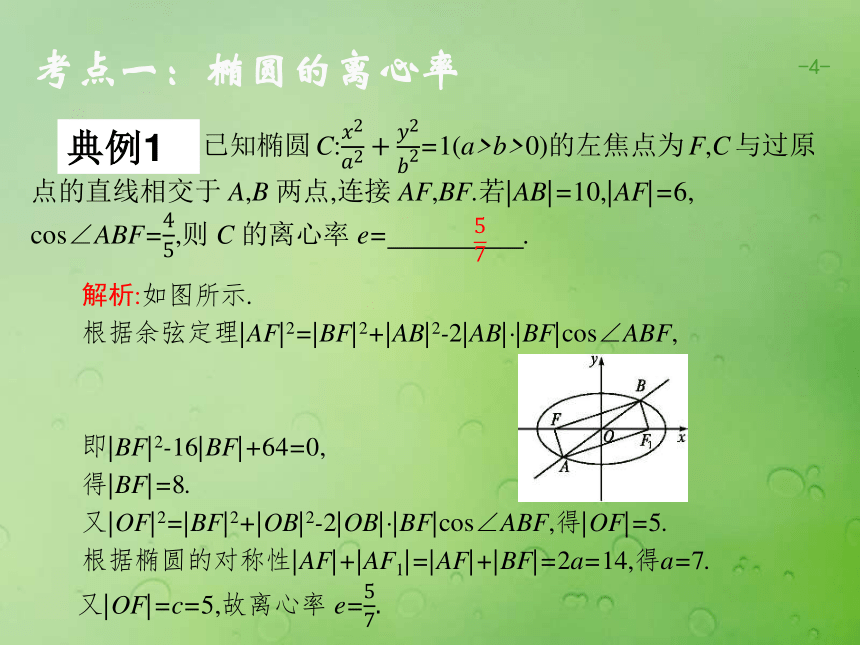
(第二课时)——离心率-1-椭圆的标准方程和几何性质 -1-2a 2b 2c c2=a2-b2 -1-解析:如图所示.
根据余弦定理|AF|2=|BF|2+|AB|2-2|AB|·|BF|cos∠ABF,
即|BF|2-16|BF|+64=0,
得|BF|=8.
又|OF|2=|BF|2+|OB|2-2|OB|·|BF|cos∠ABF,得|OF|=5.
根据椭圆的对称性|AF|+|AF1|=|AF|+|BF|=2a=14,得a=7.典例1考点一:椭圆的离心率考点一:椭圆的离心率答案:B 考点二:椭圆的离心率答案:D 考点二:椭圆的离心率答案:D 典例3考点二:椭圆的离心率答案:B -1-方法总结:求椭圆离心率,常见的三种方法:
一是通过已知条件列方程组,解出a,c的值;
二是首先已知条件列出等量关系,化出a,c的比例关系
三是由已知条件求出关于a,c的齐次方程,然后转化为关于离心率e的一元二次方程求解;
考点二:椭圆的离心率考点三:椭圆离心率的取值范围典例4:设F1,F2分别是椭圆 的左、右焦点,若该椭圆上存在的一点P,使得PF1⊥PF2,则椭圆的离心率的取值范围是________________答案:A 答案:C -1-知识小结体验高考
根据余弦定理|AF|2=|BF|2+|AB|2-2|AB|·|BF|cos∠ABF,
即|BF|2-16|BF|+64=0,
得|BF|=8.
又|OF|2=|BF|2+|OB|2-2|OB|·|BF|cos∠ABF,得|OF|=5.
根据椭圆的对称性|AF|+|AF1|=|AF|+|BF|=2a=14,得a=7.典例1考点一:椭圆的离心率考点一:椭圆的离心率答案:B 考点二:椭圆的离心率答案:D 考点二:椭圆的离心率答案:D 典例3考点二:椭圆的离心率答案:B -1-方法总结:求椭圆离心率,常见的三种方法:
一是通过已知条件列方程组,解出a,c的值;
二是首先已知条件列出等量关系,化出a,c的比例关系
三是由已知条件求出关于a,c的齐次方程,然后转化为关于离心率e的一元二次方程求解;
考点二:椭圆的离心率考点三:椭圆离心率的取值范围典例4:设F1,F2分别是椭圆 的左、右焦点,若该椭圆上存在的一点P,使得PF1⊥PF2,则椭圆的离心率的取值范围是________________答案:A 答案:C -1-知识小结体验高考
