2018年高中数学第二章圆锥曲线与方程2.4.2抛物线的几何性质课件4新人教B版选修2_1(17张)
文档属性
| 名称 | 2018年高中数学第二章圆锥曲线与方程2.4.2抛物线的几何性质课件4新人教B版选修2_1(17张) |  | |
| 格式 | zip | ||
| 文件大小 | 482.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 07:50:53 | ||
图片预览



文档简介
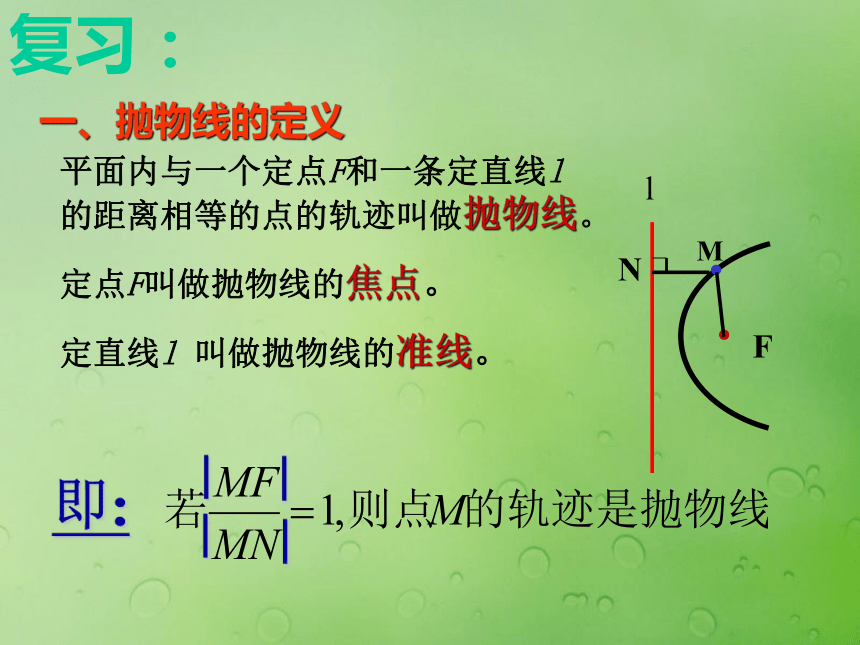
课件17张PPT。抛物线的几何性质平面内与一个定点F和一条定直线l 的距离相等的点的轨迹叫做抛物线。
定点F叫做抛物线的焦点。
定直线l 叫做抛物线的准线。
一、抛物线的定义复习:二、抛物线的标准方程焦点在x 轴上焦点在y 轴上范围
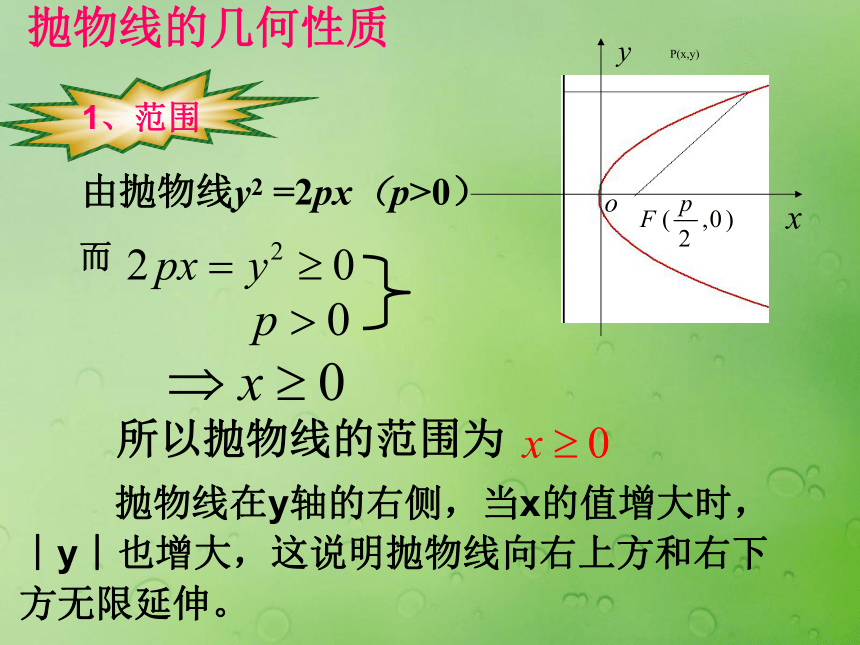
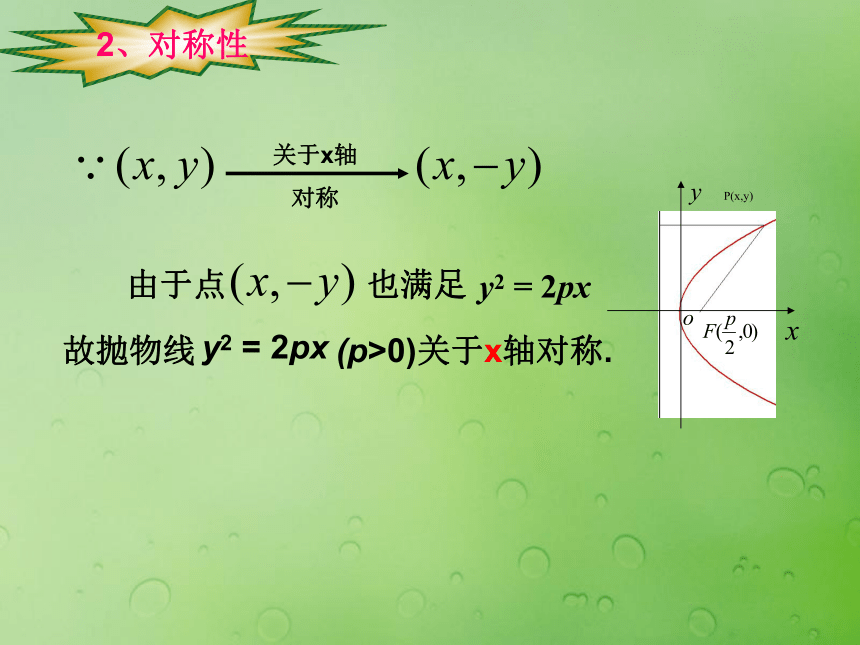
抛物线的几何性质对称性顶点离心率 抛物线的几何性质 抛物线在y轴的右侧,当x的值增大时,︱y︱也增大,这说明抛物线向右上方和右下方无限延伸。1、范围由抛物线y2 =2px(p>0)所以抛物线的范围为2、对称性定义:抛物线和它的对称轴的交点称为抛物线
的顶点。 由y2 = 2px (p>0)当y=0时,x=0, 因此抛物线的顶点就是坐标原点(0,0)。3、顶点4、离心率 抛物线上的点与焦点的距离和它到准线的距离 之比,叫做抛物线的离心率,由抛物线的定义,可知e=1。A★ 抛物线的标准方程和几何性质 x轴y轴即(0,0) 原 点e=1练习1 填表:下列抛物线的焦点坐标和准线方程
(1)y2 = 20x (2)x2= y (3)2y2 +5x =0
(4)x2 +8y =0 (5)y = -6x2 (6)(5,0)x= -5(0,-2)y=2a1练习2根据下列条件,写出抛物线的标准方程:(1)焦点是F(3,0);(2)准线方程是y = ;(4)焦点到准线的距离是2;y2 =12xx2 =yy2 =4x、 y2 = -4x、
x2 =4y 或 x2 = -4y(3)焦点在直线x-2y-4=0上。y2 =16x或x2 =-8y例1 (1)已知抛物线的顶点在原点且经过点(-3,2), x轴为对称轴,求这抛物线的方程.(2) 求顶点在原点且过点A(-3,2)的抛物线的标 准方程。解:当抛物线的焦点在y轴
的正半轴上时,把A(-3,2)
代入x2 =2py,得p= 当抛物线焦点在x轴的负半轴上时,
把A(-3,2)代入y2 = -2px,
得p=
∴抛物线的标准方程为x2 = y或y2 = x 。
例2 汽车前灯反射镜与轴截面的交线是抛物线的一部分,灯口所在的圆面与反射镜的轴垂直,灯泡位于抛物线焦点处. 已知灯口的直径是24cm,灯深10cm,那么灯泡与反射镜的顶点(即截得抛物线的顶点)距离是多少?练习1、抛物线顶点在原点,焦点在y轴上,抛物线上点P(m,-2)到焦点距离为4,则m值为( )
A 4 B -2 C 4或-4 D 12或-2C 2、设A为抛物线y2 = 4x上一点,点B(1,0)且 ,则A横坐标值为( )
A -2 B 0 C -2或0 D -2或2B 3、已知F是抛物线y2 = x的焦点,A、B是该抛物线上的两点, ,则AB中点到y轴距离为( )
A B 1 C D C小 结 : 本节课重点是抛物线的几何性质,难点是抛物线几何性质的应用。关键是正确的根据方程讨论曲线的几何性质,但要注意抛物线的性质和椭圆、双曲线的区别,抛物线的离心率等于1,它只有一个焦点、一个顶点、一条对称轴和一条准线。谢谢!
定点F叫做抛物线的焦点。
定直线l 叫做抛物线的准线。
一、抛物线的定义复习:二、抛物线的标准方程焦点在x 轴上焦点在y 轴上范围
抛物线的几何性质对称性顶点离心率 抛物线的几何性质 抛物线在y轴的右侧,当x的值增大时,︱y︱也增大,这说明抛物线向右上方和右下方无限延伸。1、范围由抛物线y2 =2px(p>0)所以抛物线的范围为2、对称性定义:抛物线和它的对称轴的交点称为抛物线
的顶点。 由y2 = 2px (p>0)当y=0时,x=0, 因此抛物线的顶点就是坐标原点(0,0)。3、顶点4、离心率 抛物线上的点与焦点的距离和它到准线的距离 之比,叫做抛物线的离心率,由抛物线的定义,可知e=1。A★ 抛物线的标准方程和几何性质 x轴y轴即(0,0) 原 点e=1练习1 填表:下列抛物线的焦点坐标和准线方程
(1)y2 = 20x (2)x2= y (3)2y2 +5x =0
(4)x2 +8y =0 (5)y = -6x2 (6)(5,0)x= -5(0,-2)y=2a1练习2根据下列条件,写出抛物线的标准方程:(1)焦点是F(3,0);(2)准线方程是y = ;(4)焦点到准线的距离是2;y2 =12xx2 =yy2 =4x、 y2 = -4x、
x2 =4y 或 x2 = -4y(3)焦点在直线x-2y-4=0上。y2 =16x或x2 =-8y例1 (1)已知抛物线的顶点在原点且经过点(-3,2), x轴为对称轴,求这抛物线的方程.(2) 求顶点在原点且过点A(-3,2)的抛物线的标 准方程。解:当抛物线的焦点在y轴
的正半轴上时,把A(-3,2)
代入x2 =2py,得p= 当抛物线焦点在x轴的负半轴上时,
把A(-3,2)代入y2 = -2px,
得p=
∴抛物线的标准方程为x2 = y或y2 = x 。
例2 汽车前灯反射镜与轴截面的交线是抛物线的一部分,灯口所在的圆面与反射镜的轴垂直,灯泡位于抛物线焦点处. 已知灯口的直径是24cm,灯深10cm,那么灯泡与反射镜的顶点(即截得抛物线的顶点)距离是多少?练习1、抛物线顶点在原点,焦点在y轴上,抛物线上点P(m,-2)到焦点距离为4,则m值为( )
A 4 B -2 C 4或-4 D 12或-2C 2、设A为抛物线y2 = 4x上一点,点B(1,0)且 ,则A横坐标值为( )
A -2 B 0 C -2或0 D -2或2B 3、已知F是抛物线y2 = x的焦点,A、B是该抛物线上的两点, ,则AB中点到y轴距离为( )
A B 1 C D C小 结 : 本节课重点是抛物线的几何性质,难点是抛物线几何性质的应用。关键是正确的根据方程讨论曲线的几何性质,但要注意抛物线的性质和椭圆、双曲线的区别,抛物线的离心率等于1,它只有一个焦点、一个顶点、一条对称轴和一条准线。谢谢!
