2018年高中数学第三章空间向量与立体几何3.2.3直线与平面的夹角课件3新人教B版选修2_1(22张)
文档属性
| 名称 | 2018年高中数学第三章空间向量与立体几何3.2.3直线与平面的夹角课件3新人教B版选修2_1(22张) |  | |
| 格式 | zip | ||
| 文件大小 | 898.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 07:53:00 | ||
图片预览



文档简介
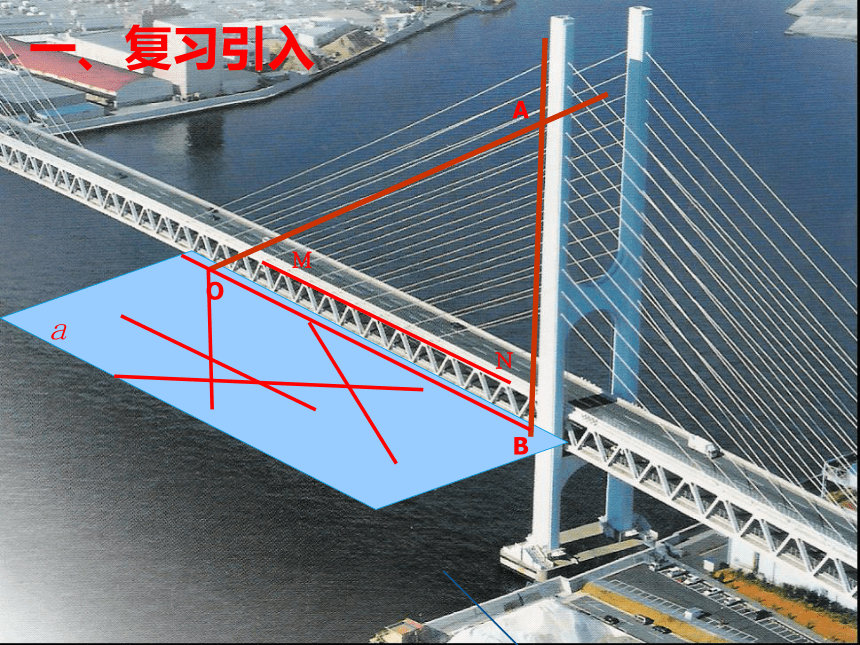
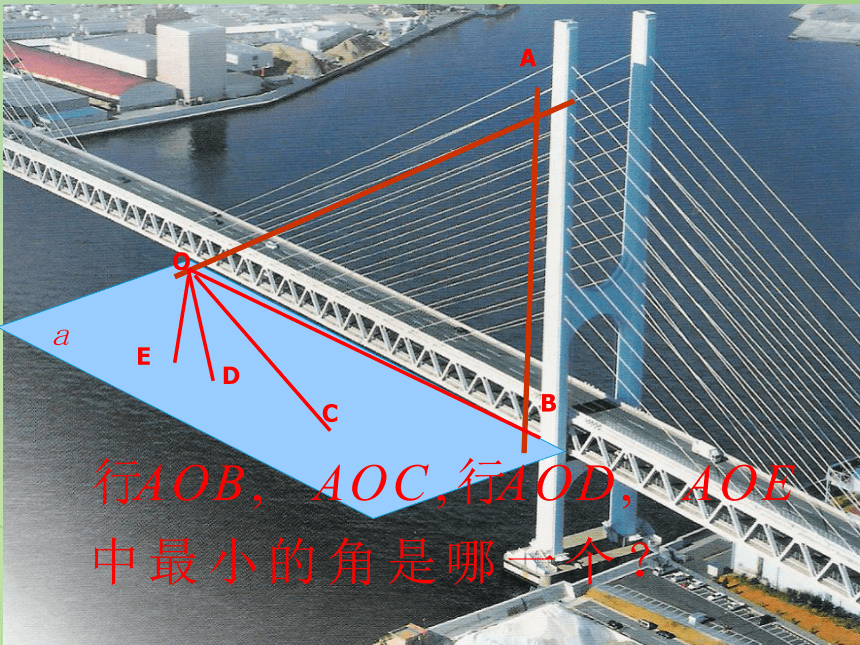
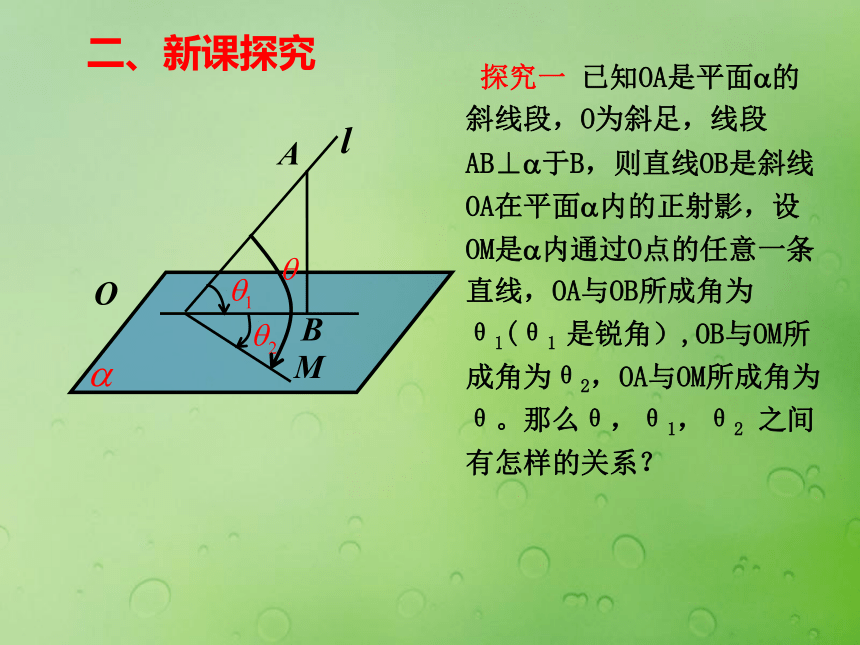
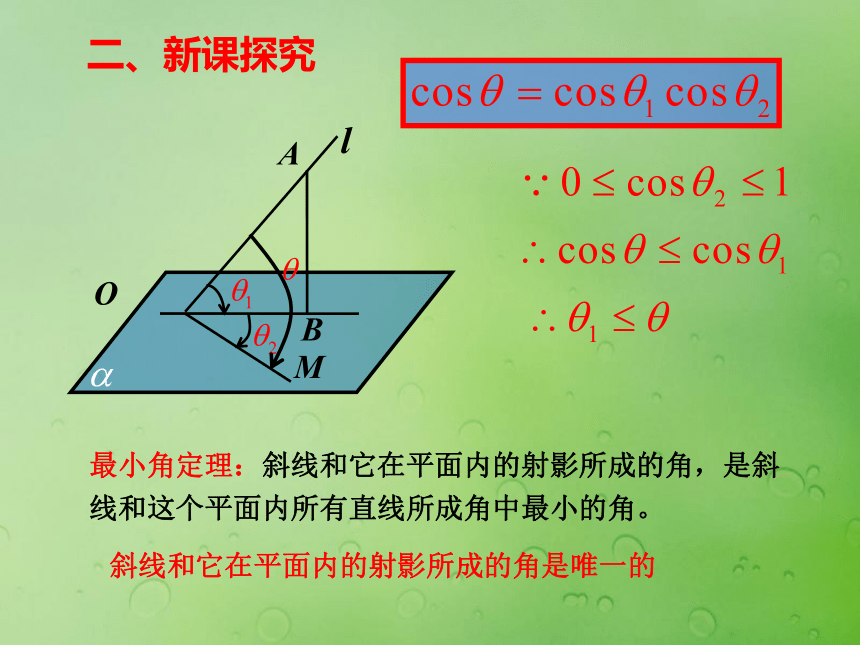
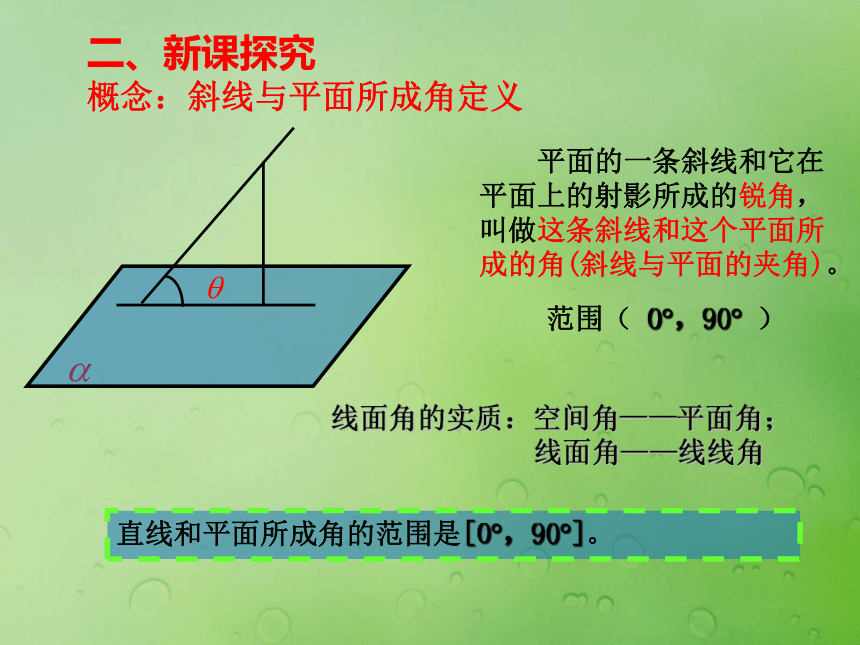
课件22张PPT。3.2.3 直线与平面的夹角Bqr6401@126.comOAB一、复习引入MNOAB二、新课探究AlBO 探究一 已知OA是平面?的斜线段,O为斜足,线段AB⊥?于B,则直线OB是斜线OA在平面?内的正射影,设OM是?内通过O点的任意一条直线,OA与OB所成角为θ1(θ1 是锐角),OB与OM所成角为θ2,OA与OM所成角为θ。那么θ,θ1,θ2 之间有怎样的关系?由于 是单位向量,故有因此在直线OM上取单位向量 ,则 ,即 。所以二、新课探究AlBO最小角定理:斜线和它在平面内的射影所成的角,是斜线和这个平面内所有直线所成角中最小的角。斜线和它在平面内的射影所成的角是唯一的二、新课探究概念:斜线与平面所成角定义 平面的一条斜线和它在平面上的射影所成的锐角,叫做这条斜线和这个平面所成的角(斜线与平面的夹角)。直线和平面所成角的范围是[0?,90?]。范围( 0?,90? )线面角的实质:空间角——平面角;
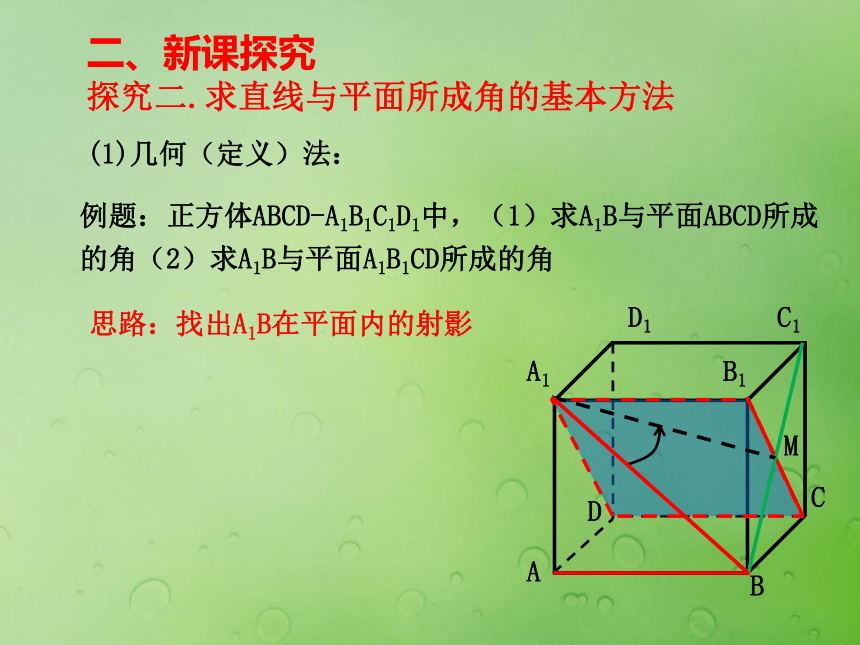
线面角——线线角二、新课探究探究二.求直线与平面所成角的基本方法(1)几何(定义)法:例题: 正方体ABCD-A1B1C1D1中,(1)求A1B与平面ABCD所成的角(2)求A1B与平面A1B1CD所成的角思路:找出A1B在平面内的射影ABCDA1B1C1D1M所以A1M是A1B在平面
A1B1CD内的射影,解:连接BC1,交B1C于M,连接A1M。在正方体ABCD-A1B1C1D1中,各面均为正方形,设其棱长为所以A1B与平面A1B1CD所成的角为30°∠BA1M为A1B与平面A1B1CD所成的角在Rt△BA1M中,二、新课探究探究二.求直线与平面所成角的基本方法 变式:正方体ABCD-A1B1C1D1中,若M,N分别是B1C1,C1D1的中点,求A1B与平面BDNM所成的角?
A1B在平面BDNM内的射影不好找,
怎么办?二、新课探究二、新课探究(2)向量求法: 变式:正方体ABCD-A1B1C1D1中,若M,N分别是B1C1,C1D1的中点,求A1B与平面BDNM所成的角? 思路:利用法向量与直线方向量所成角。ABCDD1Z解:建立如图所示坐标系,设正方形边长为1,则令 则A1(1,0,1),B(1,1,0),M(1/2,1,1),N(0,1/2,1),D(0,0,0)设平面A1B1CD的法向量为设A1B与平面A1B1CD所成的角为θ。故A1B与平面A1B1CD所成的角为45°。思 考三、新知应用例2.如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,求EB与底面ABCD所成的角正切值。 PABCDF几何法解:D(0,0,0),A(2,0,0),B(2,2,0),P(0,0,2),E(0,1,1)底面ABCD的法向量为EB与底面ABCD所成的角正切值为XYZ向量法三、新知应用例2.如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,求EB与底面ABCD所成的角正切值。 五、课堂小结知识:能力:灵活处理,分析总结,合作交流六、布置作业必做作业:课本第108页,练习A,1,2,3
探究作业:
学习进步!
线面角——线线角二、新课探究探究二.求直线与平面所成角的基本方法(1)几何(定义)法:例题: 正方体ABCD-A1B1C1D1中,(1)求A1B与平面ABCD所成的角(2)求A1B与平面A1B1CD所成的角思路:找出A1B在平面内的射影ABCDA1B1C1D1M所以A1M是A1B在平面
A1B1CD内的射影,解:连接BC1,交B1C于M,连接A1M。在正方体ABCD-A1B1C1D1中,各面均为正方形,设其棱长为所以A1B与平面A1B1CD所成的角为30°∠BA1M为A1B与平面A1B1CD所成的角在Rt△BA1M中,二、新课探究探究二.求直线与平面所成角的基本方法 变式:正方体ABCD-A1B1C1D1中,若M,N分别是B1C1,C1D1的中点,求A1B与平面BDNM所成的角?
A1B在平面BDNM内的射影不好找,
怎么办?二、新课探究二、新课探究(2)向量求法: 变式:正方体ABCD-A1B1C1D1中,若M,N分别是B1C1,C1D1的中点,求A1B与平面BDNM所成的角? 思路:利用法向量与直线方向量所成角。ABCDD1Z解:建立如图所示坐标系,设正方形边长为1,则令 则A1(1,0,1),B(1,1,0),M(1/2,1,1),N(0,1/2,1),D(0,0,0)设平面A1B1CD的法向量为设A1B与平面A1B1CD所成的角为θ。故A1B与平面A1B1CD所成的角为45°。思 考三、新知应用例2.如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,求EB与底面ABCD所成的角正切值。 PABCDF几何法解:D(0,0,0),A(2,0,0),B(2,2,0),P(0,0,2),E(0,1,1)底面ABCD的法向量为EB与底面ABCD所成的角正切值为XYZ向量法三、新知应用例2.如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,求EB与底面ABCD所成的角正切值。 五、课堂小结知识:能力:灵活处理,分析总结,合作交流六、布置作业必做作业:课本第108页,练习A,1,2,3
探究作业:
学习进步!
