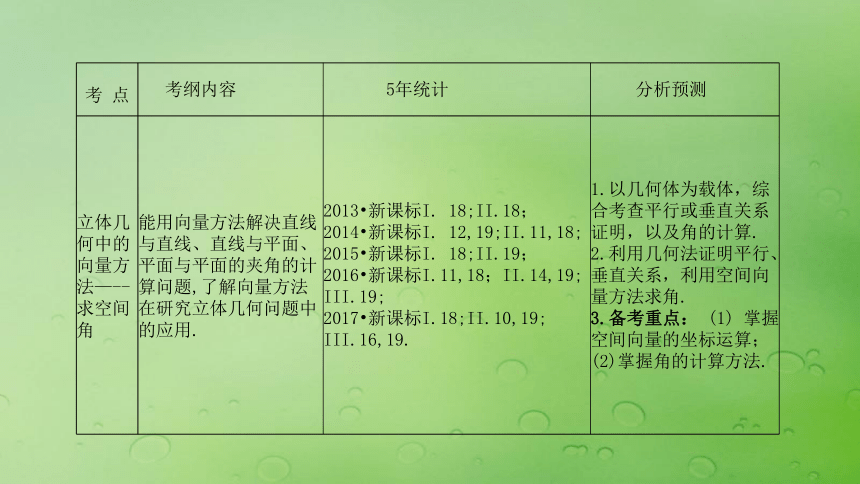
2018年高中数学第三章空间向量与立体几何3.2空间向量在立体几何中的应用课件3新人教B版选修2_1(14张)
文档属性
| 名称 | 2018年高中数学第三章空间向量与立体几何3.2空间向量在立体几何中的应用课件3新人教B版选修2_1(14张) |

|
|
| 格式 | zip | ||
| 文件大小 | 647.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 00:00:00 | ||
图片预览




文档简介
课件14张PPT。专题:立体几何中的向量方法求空间角 1. 异面直线所成的角
1.两条异面直线所成的角
③向量求法:设直线a,b的方向向量为a,b,其夹角φ,则有②范围:两异面直线所成角θ的取值范围是设a,b是两条异面直线,过空间任一点O作直线a′∥a,b′∥b,则a′与b′所夹的____________叫做a与b所成的角.①定义:锐角或直角1.长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=1,E为CC1的中点,则异面直线BC1与AE所成角的余弦值为( )【答案】B【答案】C2.已知直三棱柱 中, ,AB=2, ,,则异面直线AB1与 所成角的余弦值为( )A.D.C.B.
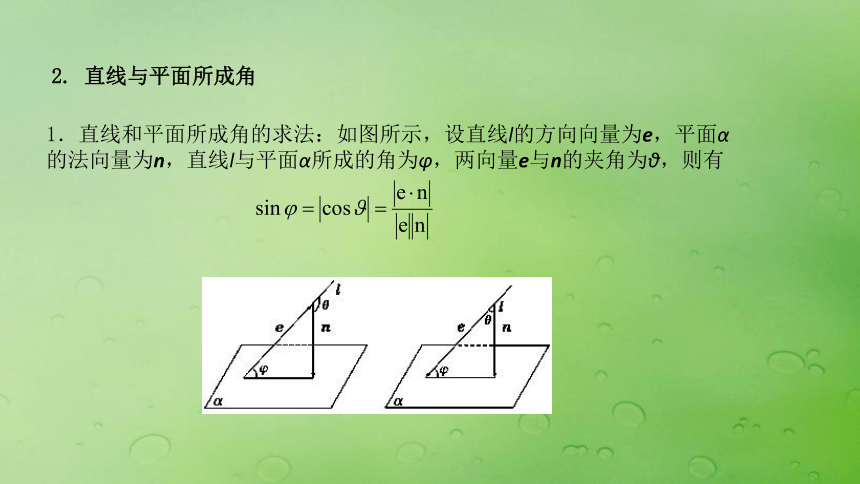
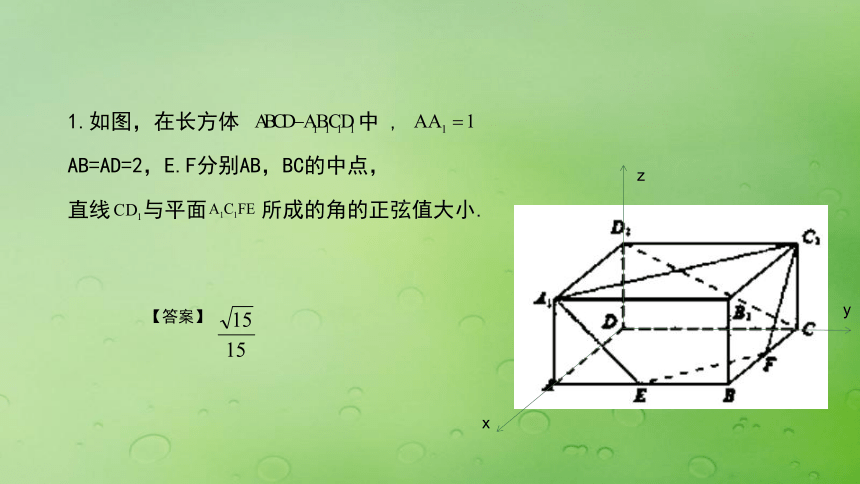
1.直线和平面所成角的求法:如图所示,设直线l的方向向量为e,平面α的法向量为n,直线l与平面α所成的角为φ,两向量e与n的夹角为θ,则有2. 直线与平面所成角1.如图,在长方体 中 ,
AB=AD=2,E.F分别AB,BC的中点,
直线 与平面 所成的角的正弦值大小. xyz【答案】2.如图,正四棱锥S-ABCD中,SA=AB= ,E,F,G分别为BC,SC,CD的中点.设P为线段FG中点.求直线BP与平面EFG所成角的正弦值.xyzO【答案】
(1)如图1,AB、CD是二面角α-l-β的两个面内与棱l垂直的直线,则二面角的大小θ=3.二面角1.求二面角的大小(2)如图2、3, 分别是二面角α-l-β的两个半平面α,β的法向量,则二面角的大小 或 .1.如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点,AP=1,AB= ,AD= ,
求二面角D-AE-C的大小。xyz【答案】2.如图,在△ABC中,∠ABC= 45°,点O在AB上,且OB=OC= AB,PO⊥平面ABC,DA∥PO, DA=AO= PO.求二面角O-CD-A的余弦值.zyx【答案】2.如图,已知在三棱柱 中,侧棱垂直于底面,AC⊥BC,BC=C1C=1/2AC=1,D是A1C1上的一点,且C1D=kA1C1.
(Ⅰ) 求证:不论k为何值,AD⊥BC;
(Ⅱ) 当k= 时,求A点到平面BCD的距离;
(Ⅲ) DB与平面ABC所成角θ的余弦值为 ,求二面角D﹣AB﹣C的正切值.zxy3.如图,已知四棱台ABCD-A1B1C1D1的上、下底面分别是边长为3和6的正方形,A1A=6,且A1A⊥底面ABCD,点P,Q分别在棱DD1,BC上.
(1)若P是DD1的中点,证明:AB1⊥PQ;
(2)若PQ∥平面ABB1A1,二角面P-QD-A的余弦值为 ,求四面体ADPQ的体积.zyx24谢谢!
1.两条异面直线所成的角
③向量求法:设直线a,b的方向向量为a,b,其夹角φ,则有②范围:两异面直线所成角θ的取值范围是设a,b是两条异面直线,过空间任一点O作直线a′∥a,b′∥b,则a′与b′所夹的____________叫做a与b所成的角.①定义:锐角或直角1.长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=1,E为CC1的中点,则异面直线BC1与AE所成角的余弦值为( )【答案】B【答案】C2.已知直三棱柱 中, ,AB=2, ,,则异面直线AB1与 所成角的余弦值为( )A.D.C.B.
1.直线和平面所成角的求法:如图所示,设直线l的方向向量为e,平面α的法向量为n,直线l与平面α所成的角为φ,两向量e与n的夹角为θ,则有2. 直线与平面所成角1.如图,在长方体 中 ,
AB=AD=2,E.F分别AB,BC的中点,
直线 与平面 所成的角的正弦值大小. xyz【答案】2.如图,正四棱锥S-ABCD中,SA=AB= ,E,F,G分别为BC,SC,CD的中点.设P为线段FG中点.求直线BP与平面EFG所成角的正弦值.xyzO【答案】
(1)如图1,AB、CD是二面角α-l-β的两个面内与棱l垂直的直线,则二面角的大小θ=3.二面角1.求二面角的大小(2)如图2、3, 分别是二面角α-l-β的两个半平面α,β的法向量,则二面角的大小 或 .1.如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点,AP=1,AB= ,AD= ,
求二面角D-AE-C的大小。xyz【答案】2.如图,在△ABC中,∠ABC= 45°,点O在AB上,且OB=OC= AB,PO⊥平面ABC,DA∥PO, DA=AO= PO.求二面角O-CD-A的余弦值.zyx【答案】2.如图,已知在三棱柱 中,侧棱垂直于底面,AC⊥BC,BC=C1C=1/2AC=1,D是A1C1上的一点,且C1D=kA1C1.
(Ⅰ) 求证:不论k为何值,AD⊥BC;
(Ⅱ) 当k= 时,求A点到平面BCD的距离;
(Ⅲ) DB与平面ABC所成角θ的余弦值为 ,求二面角D﹣AB﹣C的正切值.zxy3.如图,已知四棱台ABCD-A1B1C1D1的上、下底面分别是边长为3和6的正方形,A1A=6,且A1A⊥底面ABCD,点P,Q分别在棱DD1,BC上.
(1)若P是DD1的中点,证明:AB1⊥PQ;
(2)若PQ∥平面ABB1A1,二角面P-QD-A的余弦值为 ,求四面体ADPQ的体积.zyx24谢谢!
