2018年高中数学第一章常用逻辑用语1.2.2“非”(否定)课件1新人教B版选修2_1(15张)
文档属性
| 名称 | 2018年高中数学第一章常用逻辑用语1.2.2“非”(否定)课件1新人教B版选修2_1(15张) |  | |
| 格式 | zip | ||
| 文件大小 | 291.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 07:56:05 | ||
图片预览






文档简介
课件15张PPT。1.2 基本逻辑联结词
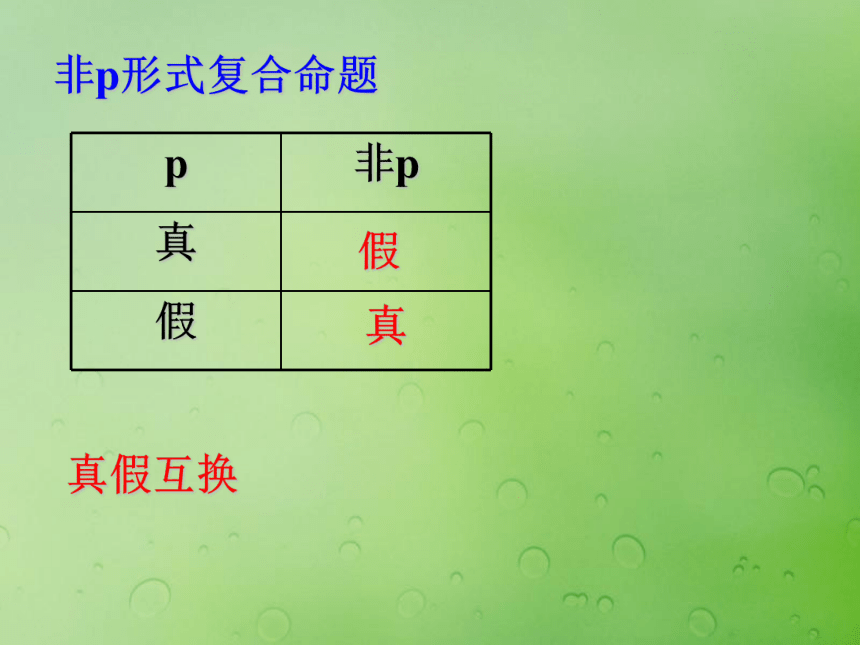
1.2.2 “非”(否定)逻辑联结词“非”(也称为“否定”)的意义是由日常语言中的“不是”“全盘否定”“问题的反面”等抽象而来的。例如:的命题“函数y=cos x的最小正周期是2π”加以否定,就构成了新的命题“函数y=cos x的最小正周期不是2π”,由此可见,如果原命题是真命题,则它的否定就应该是假命题。 一般地,对一个命题p否定,就得到一个新命题,记作读作“非p”或“p的否定”由“非”的含义,我们可以用“非”来定义集合A在全集U中的补集非p形式复合命题假真真假互换“非”命题对常见的几个正面词语的否定.1. P或q的否定形式为: ┒p且┒q2. P且q的否定形式为: ┒p或┒q3. p或q的否定形式为真命题,则p,q的真假是: ┒p且 ┒q为真命题,即p假q假4.若p或q是真命题, p且q是假命题,则p,q的真假是: p真q假 或 p假q真5.若p且q是真命题,则
p或┒q是真命题 ②┒p且┒q是假命题几种否定形式例1.写出下列各命题的非(否定),并判断其真假
(1)p:y=tan x是奇函数
(2)q:
(3)r:抛物线y=(x-1)2的顶点是(1,0)练习1:写出下列命题的非命题:(1)p:对任意实数x,均有x2-2x+1≥0;(2)q:存在一个实数x,使得x2-9=0;(3)“AB∥CD”且“AB=CD”;(4)“△ABC是直角三角形或等腰三角形”.练习2:写出下列命题的非,并判断真假:
(1)p:方程x2+1=0有实数根
(2)p:等腰三角形两底角相等
(3)点P在直线l上或点Q在直线上
(4)函数y=x3(x∈R)既是奇函数又是单调递增函数练习3. 分别写出由命题构成的“p或q”,“P且q”,“非p”形式的命题。
并判断它们的真假:
(1)p:3是质数,q:3是偶数
(2)“p:平行四边形的对角线相等”,
“q:平行四边形的对角线互相平分”
练习4.已知p:方程x2+mx+1=0有两个不等的负实根,q:方程4x2+4(m-2)x+1=0无实根,若p或q为真,p且q为假,求m的取值范围。含有量词的全称命题和存在性命题的否定例如:p:有些三角形是直角三角形。
这是一个存在性命题,用符号表示为:
? x∈{三角形},x是直角三角形
这个命题的否定是“没有一个三角形是直角三角形”,即:“所有的三角形都不是直角三角形”。
用符号表示为:┒p:? x∈{三角形},x不是直角三角形一般地,可以得出结论:存在性命题 p:? x∈A,p(x).
它的否定 ┒p:? x∈A,┒p(x).全称命题 q: ? x∈A,q(x).
它的否定 ┒q : ? x∈A, ┒q(x).即“全称肯定”的否定是“存在性否定”,另外“全称否定”的否定是“存在性肯定”.
反过来也一样.例2.写出下列命题的非,并判断其真假:
(1)p: ?x∈R,x2-x+ ≥0;
(2)q:所有的正方形都是矩形;
(3) r:? x∈R,x2+2x+2≤0;
(4) s:至少有一个实数x,使x3+1=0.练习:写出下列存在性命题的否定:
(1) p:? x∈R,x2+2x+2<0;
(2) q:有的三解形是等边三角形;
(3) r:有一个素数含三个正因数.
1.2.2 “非”(否定)逻辑联结词“非”(也称为“否定”)的意义是由日常语言中的“不是”“全盘否定”“问题的反面”等抽象而来的。例如:的命题“函数y=cos x的最小正周期是2π”加以否定,就构成了新的命题“函数y=cos x的最小正周期不是2π”,由此可见,如果原命题是真命题,则它的否定就应该是假命题。 一般地,对一个命题p否定,就得到一个新命题,记作读作“非p”或“p的否定”由“非”的含义,我们可以用“非”来定义集合A在全集U中的补集非p形式复合命题假真真假互换“非”命题对常见的几个正面词语的否定.1. P或q的否定形式为: ┒p且┒q2. P且q的否定形式为: ┒p或┒q3. p或q的否定形式为真命题,则p,q的真假是: ┒p且 ┒q为真命题,即p假q假4.若p或q是真命题, p且q是假命题,则p,q的真假是: p真q假 或 p假q真5.若p且q是真命题,则
p或┒q是真命题 ②┒p且┒q是假命题几种否定形式例1.写出下列各命题的非(否定),并判断其真假
(1)p:y=tan x是奇函数
(2)q:
(3)r:抛物线y=(x-1)2的顶点是(1,0)练习1:写出下列命题的非命题:(1)p:对任意实数x,均有x2-2x+1≥0;(2)q:存在一个实数x,使得x2-9=0;(3)“AB∥CD”且“AB=CD”;(4)“△ABC是直角三角形或等腰三角形”.练习2:写出下列命题的非,并判断真假:
(1)p:方程x2+1=0有实数根
(2)p:等腰三角形两底角相等
(3)点P在直线l上或点Q在直线上
(4)函数y=x3(x∈R)既是奇函数又是单调递增函数练习3. 分别写出由命题构成的“p或q”,“P且q”,“非p”形式的命题。
并判断它们的真假:
(1)p:3是质数,q:3是偶数
(2)“p:平行四边形的对角线相等”,
“q:平行四边形的对角线互相平分”
练习4.已知p:方程x2+mx+1=0有两个不等的负实根,q:方程4x2+4(m-2)x+1=0无实根,若p或q为真,p且q为假,求m的取值范围。含有量词的全称命题和存在性命题的否定例如:p:有些三角形是直角三角形。
这是一个存在性命题,用符号表示为:
? x∈{三角形},x是直角三角形
这个命题的否定是“没有一个三角形是直角三角形”,即:“所有的三角形都不是直角三角形”。
用符号表示为:┒p:? x∈{三角形},x不是直角三角形一般地,可以得出结论:存在性命题 p:? x∈A,p(x).
它的否定 ┒p:? x∈A,┒p(x).全称命题 q: ? x∈A,q(x).
它的否定 ┒q : ? x∈A, ┒q(x).即“全称肯定”的否定是“存在性否定”,另外“全称否定”的否定是“存在性肯定”.
反过来也一样.例2.写出下列命题的非,并判断其真假:
(1)p: ?x∈R,x2-x+ ≥0;
(2)q:所有的正方形都是矩形;
(3) r:? x∈R,x2+2x+2≤0;
(4) s:至少有一个实数x,使x3+1=0.练习:写出下列存在性命题的否定:
(1) p:? x∈R,x2+2x+2<0;
(2) q:有的三解形是等边三角形;
(3) r:有一个素数含三个正因数.
