沪科版九年级数学上册第22章相似形单元测试题(含答案)
文档属性
| 名称 | 沪科版九年级数学上册第22章相似形单元测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 115.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 14:59:34 | ||
图片预览


文档简介
沪科版九年级数学上册 第22章 相似形 单元测试题
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
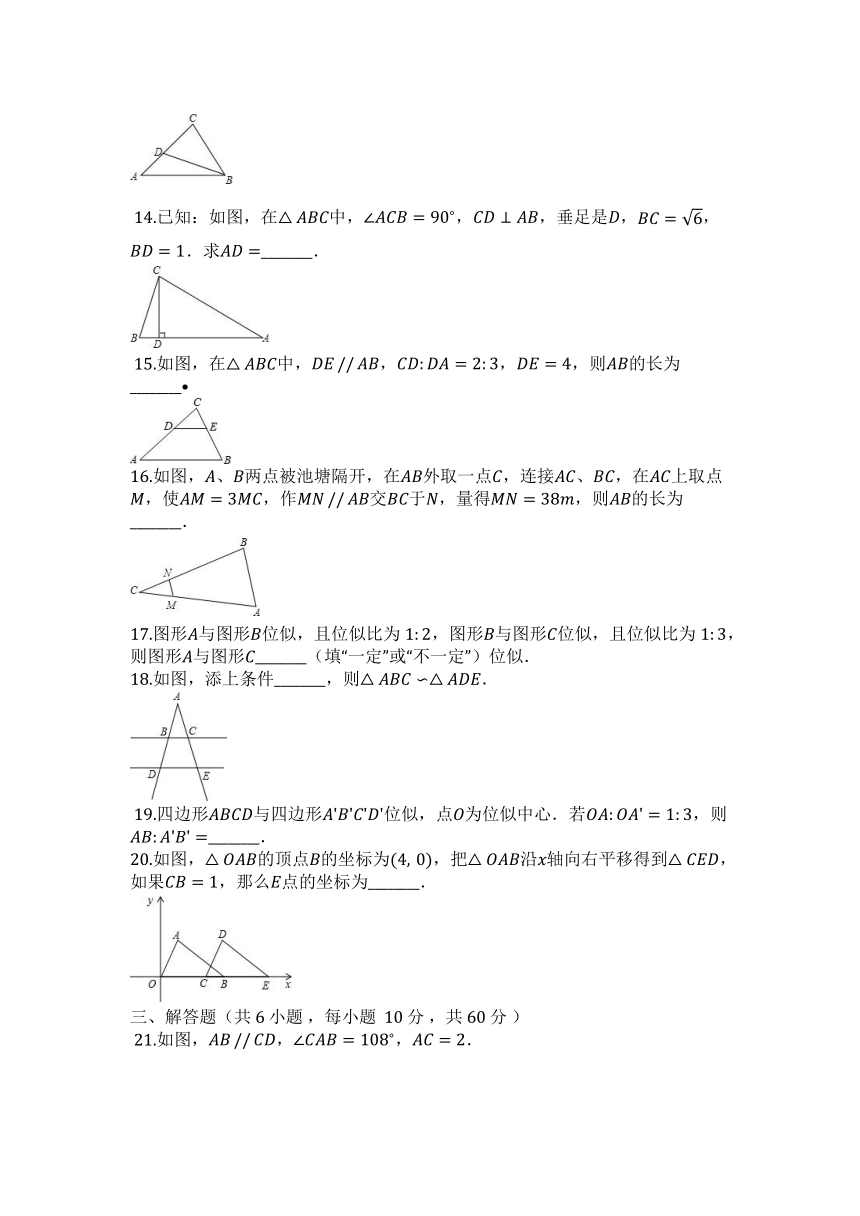
?1.如图,已知点是线段的黄金分割点,且.若表示以为边的正方形面积,表示长为、宽为的矩形面积,则与的大小关系为( )
A. B. C. D.不能确定
?2.如图,、分别是的边、上的点,,若,则的值为( )
A. B. C. D.
?3.如图,已知,,,那么下列结论正确的是( )
A. B.
C. D.
?4.如图,是斜靠在墙上的一个梯子,梯脚距墙,梯上点距墙,长,则梯子的长为( )
A. B. C. D.
?5.如果一个三角形能够分成两个与原三角形都相似的三角形,我们把这样的三角形称为孪生三角形,那么孪生三角形是( )
A.不存在 B.等腰三角形
C.直角三角形 D.等腰三角形或直角三角形
?6.在中,、分别是边、上的点,且,已知,那么等于( )
A. B. C. D.
?7.如图,中,在上,是的中点,连并延长交于,已知,则等于( )
A. B. C. D.
?8.如图,,则下列式子:①;②;③.其中一定成立的有( )
A.个 B.个 C.个 D.个
?9.下列判断正确的是( )
A.所有的直角三角形都相似 B.所有的等腰直角三角形都相似
C.所有的菱形都相似 D.所有的矩形都相似
?10.如图,梯形中,,对角线、相交于,下面四个结论:
①②③④.其中结论始终正确的有( )
A.个 B.个 C.个 D.个
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.如图,小东设计两个直角,来测量河宽,他量得,,,则河宽________.
?12.如图,是的斜边上异于、的一定点,过点作直线截交于点,使截得的与相似.已知,,,则________.
?13.如图,,,,则________.
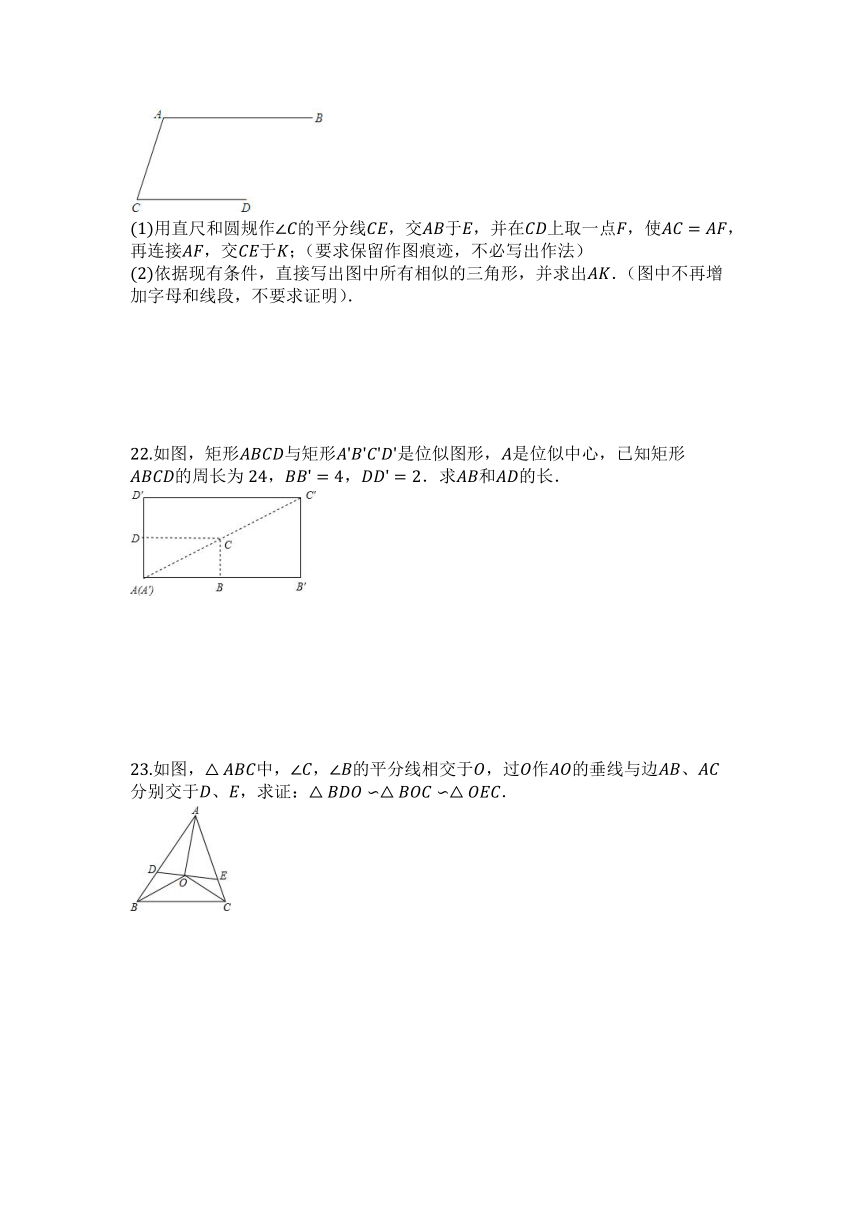
?14.已知:如图,在中,,,垂足是,,.求________.
?15.如图,在中,,,,则的长为________?
?
16.如图,、两点被池塘隔开,在外取一点,连接、,在上取点,使,作交于,量得,则的长为________.
?
17.图形与图形位似,且位似比为,图形与图形位似,且位似比为,则图形与图形________(填“一定”或“不一定”)位似.?
18.如图,添上条件________,则.
?19.四边形与四边形位似,点为位似中心.若,则________.
20.如图,的顶点的坐标为,把沿轴向右平移得到,如果,那么点的坐标为________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.如图,,,.
用直尺和圆规作的平分线,交于,并在上取一点,使,再连接,交于;(要求保留作图痕迹,不必写出作法)
依据现有条件,直接写出图中所有相似的三角形,并求出.(图中不再增加字母和线段,不要求证明).
?
22.如图,矩形与矩形是位似图形,是位似中心,已知矩形的周长为,,.求和的长.
?
23.如图,中,,的平分线相交于,过作的垂线与边、分别交于、,求证:.
?
24.如图,在中,已知,,,.
求的值;
求的长.
?
25.如图,在四边形中,平分,.
求证:;
若,,求线段的长.
?
26.如图,已知,,,,,
求的长;
求的大小.
答案
1.B
2.D
3.B
4.A
5.C
6.D
7.C
8.B
9.B
10.B
11.
12.或
13.
14.
15.
16.
17.不一定
18.等
19.
20.
21.解:(1)作法正确得,点作法正确得,点标注正确得;
(2);
理由:∵,,
∴,
∴,
∵,
∴,
∵,
∴,
∴,,
∴,.
∵,
∴,
∵,
∴,
解得:,(不可能是负数),
∴.
22.解:设,
∵矩形的周长为,
∴,
∵,,
∴,,
∵矩形与矩形是位似图形,
∴,
即,
解得:,
经检验,是原分式方程的解.
∴,.
23.证明:∵,的平分线相交于,
∴,,平分,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
同理:,
∴.
24.解:∵,
∴
∴;∵
∴
∴
∵
∴
∴.
25.证明:∵平分,
∴,
∵,
∴,
,
∴;解:由知,,
∵,,
∴,
∵,
.
26.解:∵,
∴,
∴,
解得:;∵,
∴,,
∴.
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.如图,已知点是线段的黄金分割点,且.若表示以为边的正方形面积,表示长为、宽为的矩形面积,则与的大小关系为( )
A. B. C. D.不能确定
?2.如图,、分别是的边、上的点,,若,则的值为( )
A. B. C. D.
?3.如图,已知,,,那么下列结论正确的是( )
A. B.
C. D.
?4.如图,是斜靠在墙上的一个梯子,梯脚距墙,梯上点距墙,长,则梯子的长为( )
A. B. C. D.
?5.如果一个三角形能够分成两个与原三角形都相似的三角形,我们把这样的三角形称为孪生三角形,那么孪生三角形是( )
A.不存在 B.等腰三角形
C.直角三角形 D.等腰三角形或直角三角形
?6.在中,、分别是边、上的点,且,已知,那么等于( )
A. B. C. D.
?7.如图,中,在上,是的中点,连并延长交于,已知,则等于( )
A. B. C. D.
?8.如图,,则下列式子:①;②;③.其中一定成立的有( )
A.个 B.个 C.个 D.个
?9.下列判断正确的是( )
A.所有的直角三角形都相似 B.所有的等腰直角三角形都相似
C.所有的菱形都相似 D.所有的矩形都相似
?10.如图,梯形中,,对角线、相交于,下面四个结论:
①②③④.其中结论始终正确的有( )
A.个 B.个 C.个 D.个
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.如图,小东设计两个直角,来测量河宽,他量得,,,则河宽________.
?12.如图,是的斜边上异于、的一定点,过点作直线截交于点,使截得的与相似.已知,,,则________.
?13.如图,,,,则________.
?14.已知:如图,在中,,,垂足是,,.求________.
?15.如图,在中,,,,则的长为________?
?
16.如图,、两点被池塘隔开,在外取一点,连接、,在上取点,使,作交于,量得,则的长为________.
?
17.图形与图形位似,且位似比为,图形与图形位似,且位似比为,则图形与图形________(填“一定”或“不一定”)位似.?
18.如图,添上条件________,则.
?19.四边形与四边形位似,点为位似中心.若,则________.
20.如图,的顶点的坐标为,把沿轴向右平移得到,如果,那么点的坐标为________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.如图,,,.
用直尺和圆规作的平分线,交于,并在上取一点,使,再连接,交于;(要求保留作图痕迹,不必写出作法)
依据现有条件,直接写出图中所有相似的三角形,并求出.(图中不再增加字母和线段,不要求证明).
?
22.如图,矩形与矩形是位似图形,是位似中心,已知矩形的周长为,,.求和的长.
?
23.如图,中,,的平分线相交于,过作的垂线与边、分别交于、,求证:.
?
24.如图,在中,已知,,,.
求的值;
求的长.
?
25.如图,在四边形中,平分,.
求证:;
若,,求线段的长.
?
26.如图,已知,,,,,
求的长;
求的大小.
答案
1.B
2.D
3.B
4.A
5.C
6.D
7.C
8.B
9.B
10.B
11.
12.或
13.
14.
15.
16.
17.不一定
18.等
19.
20.
21.解:(1)作法正确得,点作法正确得,点标注正确得;
(2);
理由:∵,,
∴,
∴,
∵,
∴,
∵,
∴,
∴,,
∴,.
∵,
∴,
∵,
∴,
解得:,(不可能是负数),
∴.
22.解:设,
∵矩形的周长为,
∴,
∵,,
∴,,
∵矩形与矩形是位似图形,
∴,
即,
解得:,
经检验,是原分式方程的解.
∴,.
23.证明:∵,的平分线相交于,
∴,,平分,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
同理:,
∴.
24.解:∵,
∴
∴;∵
∴
∴
∵
∴
∴.
25.证明:∵平分,
∴,
∵,
∴,
,
∴;解:由知,,
∵,,
∴,
∵,
.
26.解:∵,
∴,
∴,
解得:;∵,
∴,,
∴.
