江苏省镇江市2019届高三上学期期中考试数学理试题(小题解析)
文档属性
| 名称 | 江苏省镇江市2019届高三上学期期中考试数学理试题(小题解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 768.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-25 00:00:00 | ||
图片预览




文档简介
镇江大市统考2019届高三期中考试
数学理科
一、填空题
1、设集合A={x|x是小于4的偶数},
考点:集合的运算。
答案:{2}
解析:集合B中小于4的偶数只有2,所以,{2}
2、命题的否定为
考点:命题的否定。
答案:
解析:把任意改为存在,并否定结论。
3、若复数是纯虚数,则
考点:复数的运算,纯虚数的概念。
答案:2
解析:,
因为z是纯虚数,所以,2-=0,即=2,经检验=2时z为纯虚数。
4、函数的定义域为
考点:对数的函数的定义,一元二次不等式的解法。
答案:
解析:由对数函数定义,得:>0,即(x-1)(x-3)>0,解得:x<1或x>3。
5、在△ABC中,分别为角A,B,C的对边,且A=45°,C=75°,=1,则b=__
考点:正弦定理。
答案:
解析:B=180°-45°-75°=60°,由正弦定理,得:
,解得:b=
6、已知函数是奇函数,则f(-1)+f(0)=____
考点:奇函数的性质。
答案:
解析:函数的定义域为R,是奇函数,所以,有=0,
即=0,解得:,
=
7、已知e为自然对数的底数,函数y=ex-lnx在[1,e]的最小值为__
考点:函数的导数及其应用。
答案:e
解析:求导,得:=0,得,当x在(时,>0,函数y是增函数
所以,y在[1,e]的最小值为:e-ln1=e
8、已知函数在上是增函数,则的取值范围为
考点:二次函数的图象及其性质。
答案:[12,+∞)
解析:函数图象的开口向上,对称轴为:,
因为在上是增函数,所以,-1,
,
所以,的取值范围为[12,+∞)
9、将函数的图象向左平移个单位后,所得函数图象关于直线对称,则=
考点:正函数的图象及其变换。
答案:
解析:函数的图象向左平移个单位后为:,
平移后函数图象关于直线对称,
所以,,即:,
又,所以,令k=1,得:。
10、在中,已知,则
考点:两角和的正切函数运算,余弦函数。
答案:
解析:由题,有:,即:,
tan(A+B)==1,所以,A+B=,,
cosC==
11、已知的最小值为
考点:基本不等式。
答案:
解析:由,得:,
==
==
当,即时,取等号。
所以,的最小值为
12、已知函数则不等式的解集为
考点:函数的奇偶性、单调性,指数函数的性质,分类讨论的数学思想。
答案:
解析:因为,所以,为偶函数,
,
易知,在[0,+∞)是增函数,在(-∞,0)上是减函数。
因为,
(1)当x>1时,有,即2<,所以,x>100
(2)当0<x<1时,有-2>,所以,0<x<,
所以,不等式的解集为
13、在中,角对边分别为,已知,则的最小值
考点:同角三角函数的变换,三角恒等变换,基本不等式,正弦定理,余弦定理。
答案:
解析:由,得:
,去分母,得:
,
即:
即:,由正弦定理,得:
cosC===
当且仅当时,取等号,
所以,的最小值为
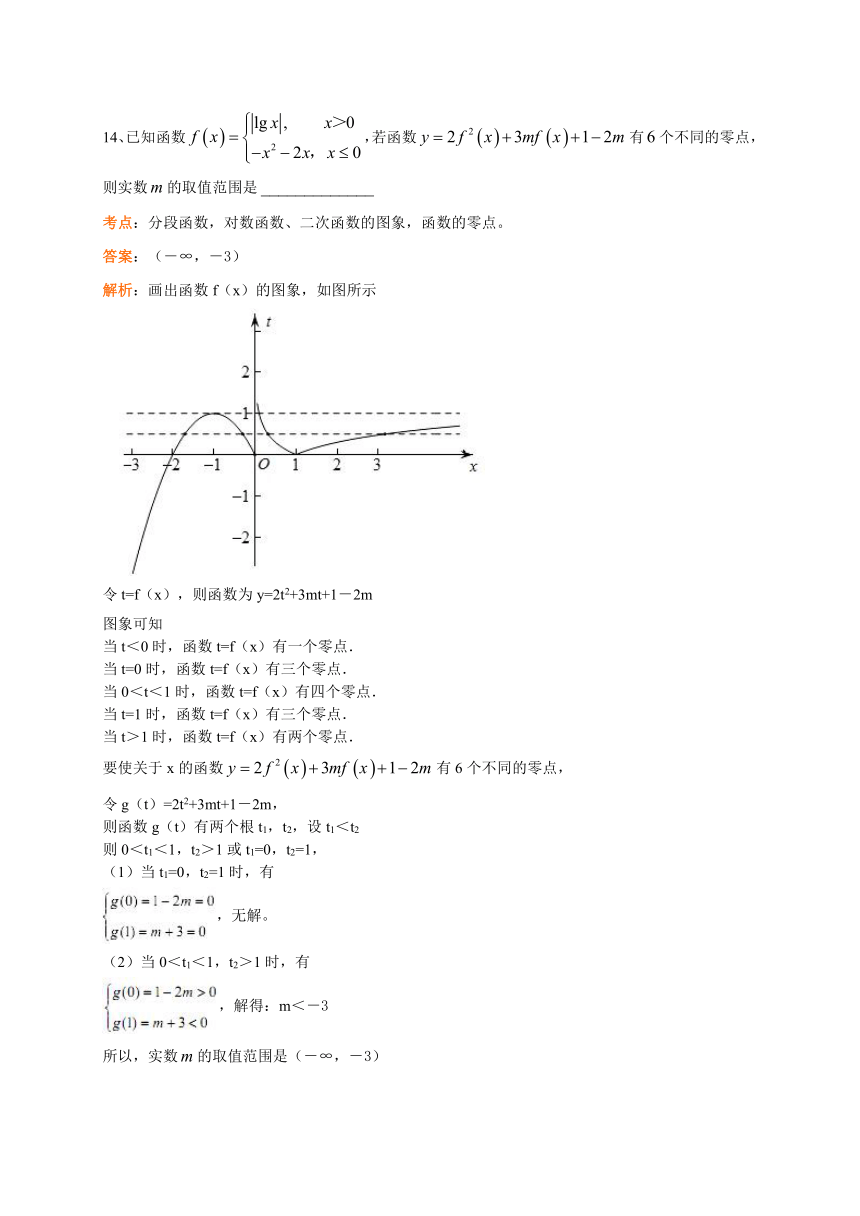
14、已知函数,若函数有个不同的零点,则实数的取值范围是
考点:分段函数,对数函数、二次函数的图象,函数的零点。
答案:(-∞,-3)
解析:画出函数f(x)的图象,如图所示
令t=f(x),则函数为y=2t2+3mt+1-2m
图象可知
当t<0时,函数t=f(x)有一个零点.
当t=0时,函数t=f(x)有三个零点.
当0<t<1时,函数t=f(x)有四个零点.
当t=1时,函数t=f(x)有三个零点.
当t>1时,函数t=f(x)有两个零点.
要使关于x的函数有6个不同的零点,
令g(t)=2t2+3mt+1-2m,
则函数g(t)有两个根t1,t2,设t1<t2
则0<t1<1,t2>1或t1=0,t2=1,
(1)当t1=0,t2=1时,有
,无解。
(2)当0<t1<1,t2>1时,有
,解得:m<-3
所以,实数的取值范围是(-∞,-3)
2、解答题(90分)
15、(本小题满分14分)
在中,角,,的对边为,,,且
求角
若,求的值
.(本小题满分14分)
已知,函数
解关于的不等式
对任意恒成立,求实数的取值范围
17、(本小题满分14分)
已知函数且1)为增函数。
(1)求实数的取值范围;
(2)当=4时,是否存在正实数m,n(m<n),使得函数f(x)的定义域为[m,n],值域为?如果存在,求出所有的m,n,如果不存在,请说明理由。
18.(本小题满分16分)
如图,郊外有一边长为200m的菱形池塘ABCD,,塘边AB与AD的夹角为60°,拟架设三条网隔把池塘分成几个不同区域,其中网隔相互垂直,两点分别在塘边上,区域为荷花种植区域,记荷花种植区域面积为.
(1)求的函数关系式;
(2)求的最小值.
19.(本小题满分16分)
已知函数
(1)若函数为奇函数,求实数的值;
(2)若对任意的[-1,1],不等式在[-1,1]恒成立,求实数m的取值范围。
(3)若在处取得极小值,且(0,3),求实数的取值范围。
20.(本小题满分16分)
已知函数为自然对数的底数。
(1)如果函数在上单调递增,求实数的取值范围;
(2)若直线是函数图像的一条切线,求实数的值;
(3)设且求证:
参考答案
1、{2} 2、 3、2 4、 5、
6、 7、e 8、[12,+∞) 9、 10、
11、 12、 13、 14、(-∞,-3)
15、
16、
17、
18、
19、
20
同课章节目录
