2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.1.2椭圆的几何性质课件(47张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.1.2椭圆的几何性质课件(47张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 00:00:00 | ||
图片预览






文档简介
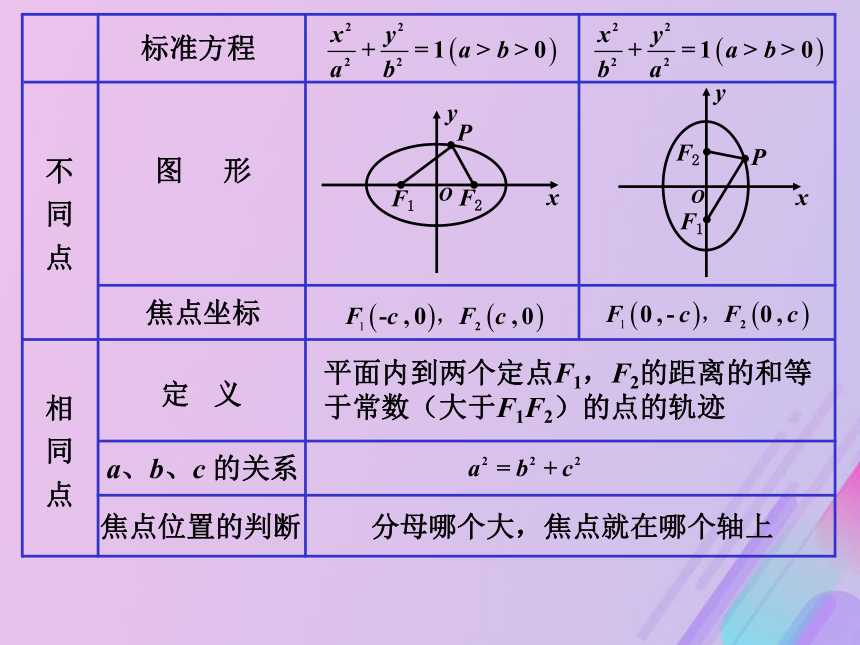
课件47张PPT。椭圆的简单几何性质复习:1.椭圆的定义: 平面内,到两定点F1、F2的距离之和为常数(大于|F1F2 |)的动点的轨迹叫做椭圆。2.椭圆的标准方程是:3.椭圆中a,b,c的关系是:a2=b2+c2当焦点在X轴上时当焦点在Y轴上时分母哪个大,焦点就在哪个轴上平面内到两个定点F1,F2的距离的和等
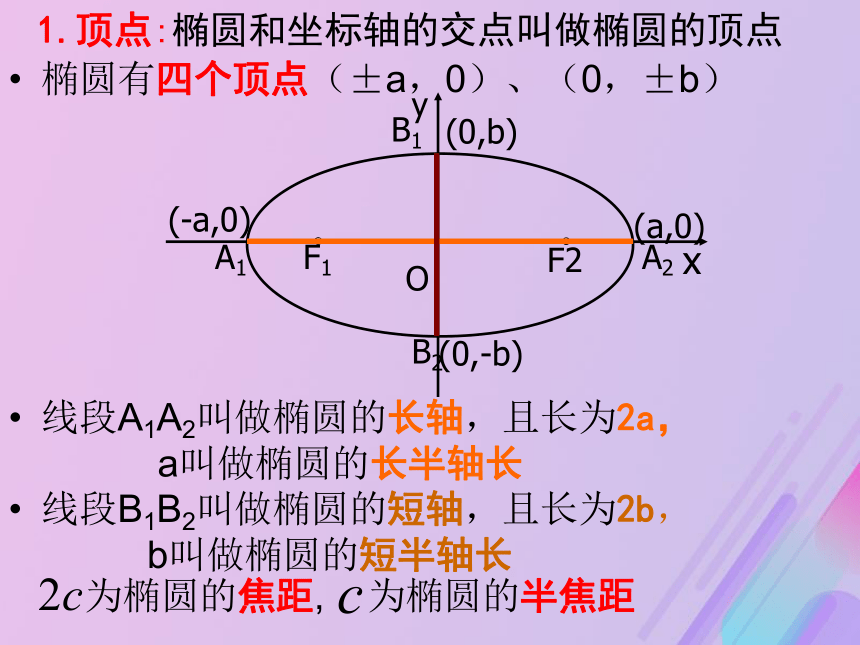
于常数(大于F1F2)的点的轨迹1.顶点:椭圆和坐标轴的交点叫做椭圆的顶点椭圆有四个顶点(±a,0)、(0,±b)
线段A1A2叫做椭圆的长轴,且长为2a,
a叫做椭圆的长半轴长
线段B1B2叫做椭圆的短轴,且长为2b,
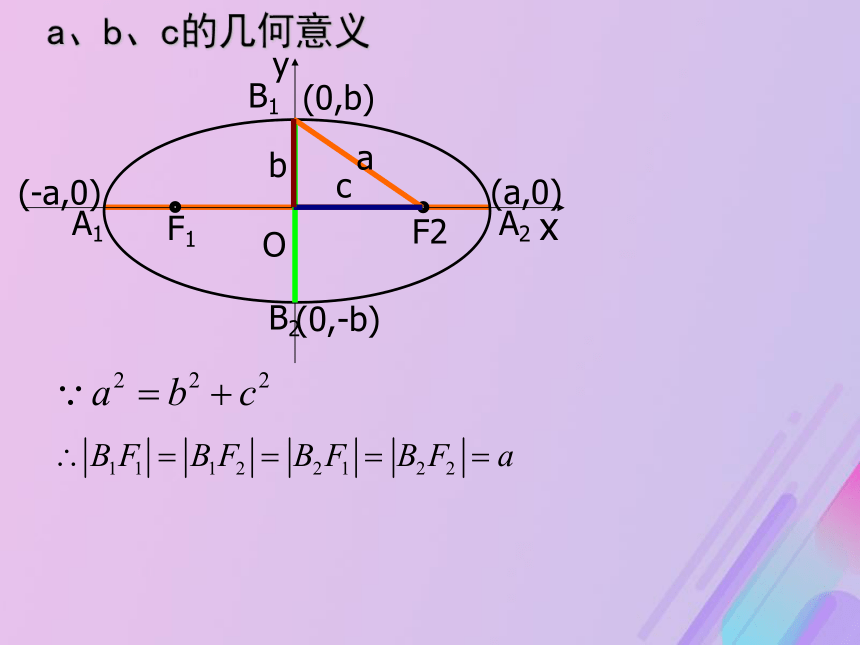
b叫做椭圆的短半轴长O x F1 F2 A2B1 B2 y A1(-a,0) (a,0) (0,b) (0,-b) O x F1 A2B1 B2 y A1(-a,0) (a,0) (0,b) (0,-b) a、b、c的几何意义a c b F2 -a≤x≤a, -b≤y≤b 知
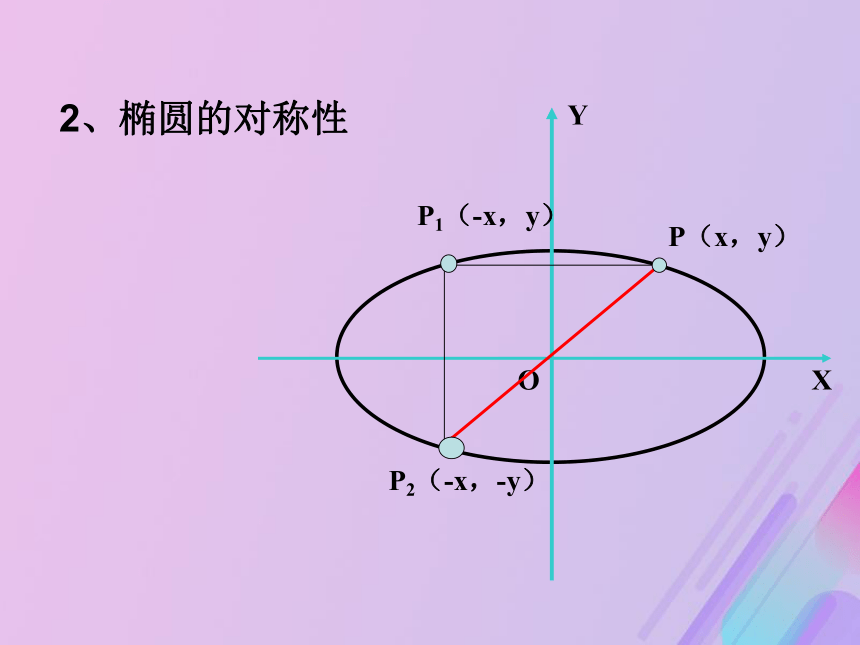
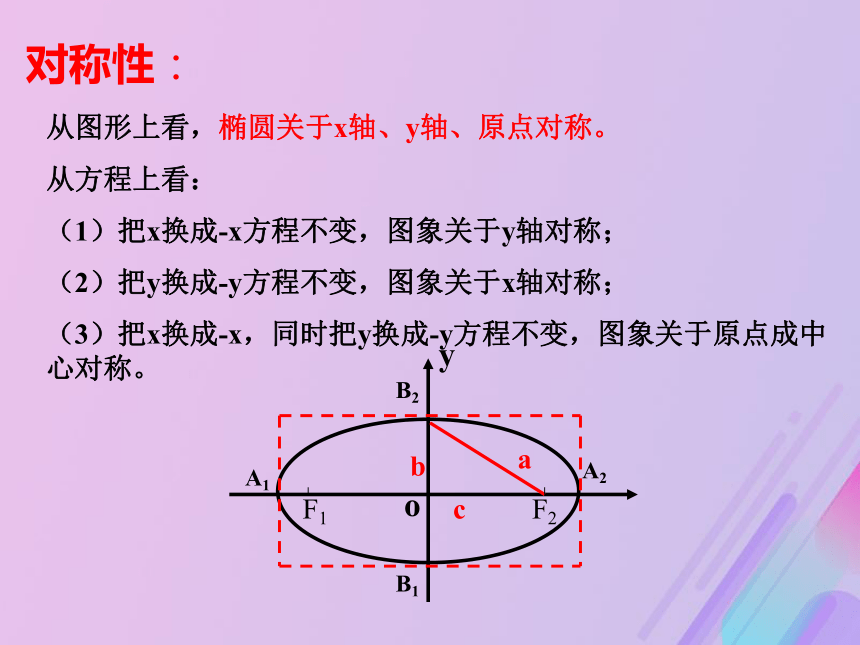
椭圆落在x=±a,y= ± b组成的矩形中2、范围:2、椭圆的对称性对称性:从图形上看,椭圆关于x轴、y轴、原点对称。
从方程上看:
(1)把x换成-x方程不变,图象关于y轴对称;
(2)把y换成-y方程不变,图象关于x轴对称;
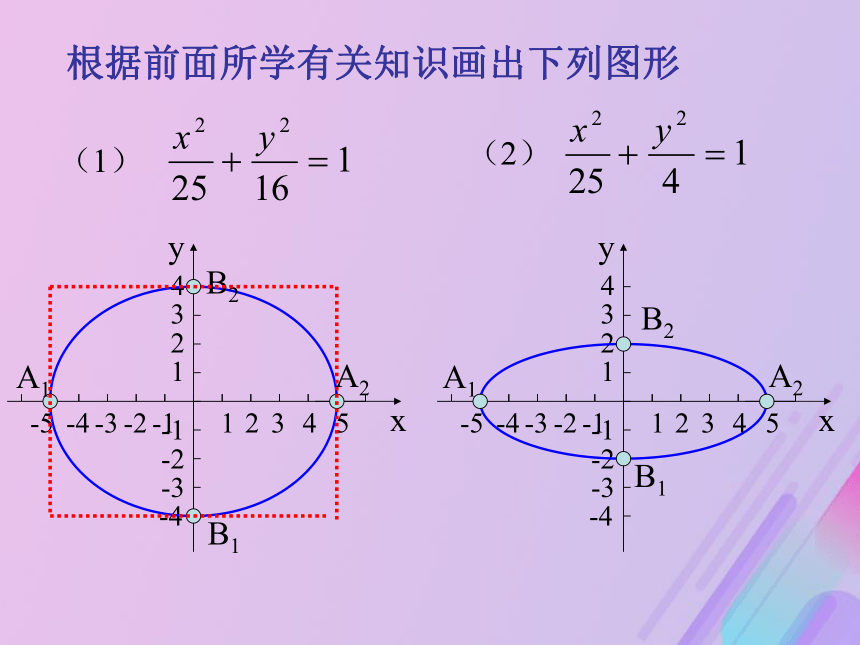
(3)把x换成-x,同时把y换成-y方程不变,图象关于原点成中心对称。根据前面所学有关知识画出下列图形(1)(2)A1 B1 A2 B2 B2 A2 B1 A1 4、椭圆的离心率 (刻画椭圆扁平程度的量)[1]离心率的取值范围:[2]离心率对椭圆形状的影响:0当e=1时曲线又是 什么?圆线段F1F2两种标准方程的椭圆性质的比较关于x轴、y轴、原点对称A1(-a,0), A2(a,0)
B1(0,-b), B2(0,b)A1(0,-a), A2(0,a)
B1(-b,0), B2(b,0)例1求椭圆16x2+25y2=400的长轴和短轴长,离心率,焦点和顶点坐标。解:把已知方程化为标准方程椭圆的四个顶点是A1(-5,0)、A2(5,0)、
B1(0,-4)、B2(0,4) 焦点F1(-3,0)和F2(3,0),练习:
求下列椭圆的长轴长、短轴长、焦点坐标、顶点坐标和离心率。
(1)x2+9y2=81 (2) 25x2+9y2=225
(3) 16x2+y2=25 (4) 4x2+5y2=1例2:点M(x,y)与定点F(4,0)的距离和它到直
线 的距离的比是常数 ,求点M的轨迹。练习:P50 T2椭圆的第二定义:平面内到定点(焦点)的距离和它到定直线(准线)的距离的比是一个常数(离心率)(0<常数<1)的点的轨迹是椭圆例3 求适合下列条件的椭圆的标准方程
⑴经过点P(-3,0)、Q(0,-2);
⑵长轴长等于20,离心率3/5。
⑶一焦点将长轴分成2:1的两部分,且经过点解: ⑴方法一:设方程为mx2+ny2=1(m>0,n>0,m≠n),将点的坐标方程,求出m=1/9,n=1/4。方法二:利用椭圆的几何性质,以坐标轴为对称轴的椭圆与坐标轴的交点就是椭圆的顶点,于是焦点在x轴上,且点P、Q分别是椭圆长轴与短轴的一个端点
,故a=3,b=2,所以椭圆的标准方程为 注:待定系数法求椭圆标准方程的步骤: ⑴定型; ⑵定量作业:P49 T51. 已知椭圆的一个焦点为F(6,0)点B,C是短轴的两端点,△FBC是等边三角形,求这个椭圆的标准方程。例4:(1)椭圆 的左焦点
是两个顶点,如果到F1直线AB的
距 离为 ,则椭圆的离心率e= .题型三:椭圆的离心率问题例4:(2)设M为椭圆 上一点, 为椭圆的焦点,
如果 ,求椭圆的离心率。练习:D2若椭圆两准线间的距离等于焦距的4倍,则这个椭圆的离心率是( )D2.2.2 椭圆的简单几何性质1-----点、直线与椭圆的位置关系2-----弦长公式(第三课时)探究点与椭圆有几种位置关系,该怎样判断呢?类比圆可以吗?点与椭圆的位置关系D练一下回忆:直线与圆的位置关系1.位置关系:相交、相切、相离
2.判别方法(代数法)
联立直线与椭圆的方程
消元得到二元一次方程组
(1)△>0?直线与圆相交?有两个公共点;
(2)△=0 ?直线与圆相切?有且只有一个公共点;
(3)△<0 ?直线与圆相离?无公共点.通法3.几何法点线距d与半径r的大小关系直线与椭圆的位置关系种类:相离(没有交点)相切(一个交点)相交(二个交点)相离(没有交点)
相切(一个交点)
相交(二个交点) 直线与椭圆的位置关系的判定代数方法1.位置关系:相交、相切、相离
2.判别方法(代数法)
联立直线与椭圆的方程
消元得到二元一次方程组
(1)△>0?直线与椭圆相交?有两个公共点;
(2)△=0 ?直线与椭圆相切?有且只有一个公共点;
(3)△<0 ?直线与椭圆相离?无公共点.通法1.直线与椭圆的位置关系例1.k为何值时,直线y=kx+2和曲线2x2+3y2=6有两个公共点?有一个公共点?没有公共点?1.直线与椭圆的位置关系 B 2.无论k为何值,直线y=kx+2和曲线
交点情况满足( )
A.没有公共点 B.一个公共点
C.两个公共点 D.有公共点变式: D 思考:最大的距离是多少?1.直线与椭圆的位置关系练习:已知直线y=x- 与椭圆x2+4y2=2 ,判断它们的位置关系.解:联立方程组消去y?>0因为所以,方程(1)有两个根,那么,相交所得的弦的弦长是多少?则原方程组有两组解….----- (1)1.直线与椭圆的位置关系设直线与椭圆交于P1(x1,y1),P2(x2,y2)两点,直线P1P2的斜率为k.弦长公式:2.弦长公式
例3.已知斜率为1的直线l过椭圆 的右焦点,
交椭圆于A,B两点,求弦AB之长.2.弦长公式例 4.已知椭圆 过点P(2,1)引一弦,使弦在这点被平分,求此弦所在直线的方程.解:韦达定理→斜率韦达定理法:利用韦达定理及中点坐标公式来构造弦中点问题点差法:利用端点在曲线上,坐标满足方程,作差构造
出中点坐标和斜率.点作差弦中点问题例 4.已知椭圆 过点P(2,1)引一弦,使弦在这点被平分,求此弦所在直线的方程.例4.已知椭圆 过点P(2,1)引一弦,使弦在这点被
平分,求此弦所在直线的方程.所以 x2+4y2=(4-x)2+4(2-y)2,整理得x+2y-4=0
从而A ,B在直线x+2y-4=0上
而过A,B两点的直线有且只有一条解后反思:中点弦问题求解关键在于充分利用“中点”这一 条件,灵活运用中点坐标公式及韦达定理,弦中点问题3、弦中点问题的两种处理方法:
(1)联立方程组,消去一个未知数,利用韦达定理;
(2)设两端点坐标,代入曲线方程相减可求出弦的斜率。 1、直线与椭圆的三种位置关系及判断方法;小 结
于常数(大于F1F2)的点的轨迹1.顶点:椭圆和坐标轴的交点叫做椭圆的顶点椭圆有四个顶点(±a,0)、(0,±b)
线段A1A2叫做椭圆的长轴,且长为2a,
a叫做椭圆的长半轴长
线段B1B2叫做椭圆的短轴,且长为2b,
b叫做椭圆的短半轴长O x F1 F2 A2B1 B2 y A1(-a,0) (a,0) (0,b) (0,-b) O x F1 A2B1 B2 y A1(-a,0) (a,0) (0,b) (0,-b) a、b、c的几何意义a c b F2 -a≤x≤a, -b≤y≤b 知
椭圆落在x=±a,y= ± b组成的矩形中2、范围:2、椭圆的对称性对称性:从图形上看,椭圆关于x轴、y轴、原点对称。
从方程上看:
(1)把x换成-x方程不变,图象关于y轴对称;
(2)把y换成-y方程不变,图象关于x轴对称;
(3)把x换成-x,同时把y换成-y方程不变,图象关于原点成中心对称。根据前面所学有关知识画出下列图形(1)(2)A1 B1 A2 B2 B2 A2 B1 A1 4、椭圆的离心率 (刻画椭圆扁平程度的量)[1]离心率的取值范围:[2]离心率对椭圆形状的影响:0
B1(0,-b), B2(0,b)A1(0,-a), A2(0,a)
B1(-b,0), B2(b,0)例1求椭圆16x2+25y2=400的长轴和短轴长,离心率,焦点和顶点坐标。解:把已知方程化为标准方程椭圆的四个顶点是A1(-5,0)、A2(5,0)、
B1(0,-4)、B2(0,4) 焦点F1(-3,0)和F2(3,0),练习:
求下列椭圆的长轴长、短轴长、焦点坐标、顶点坐标和离心率。
(1)x2+9y2=81 (2) 25x2+9y2=225
(3) 16x2+y2=25 (4) 4x2+5y2=1例2:点M(x,y)与定点F(4,0)的距离和它到直
线 的距离的比是常数 ,求点M的轨迹。练习:P50 T2椭圆的第二定义:平面内到定点(焦点)的距离和它到定直线(准线)的距离的比是一个常数(离心率)(0<常数<1)的点的轨迹是椭圆例3 求适合下列条件的椭圆的标准方程
⑴经过点P(-3,0)、Q(0,-2);
⑵长轴长等于20,离心率3/5。
⑶一焦点将长轴分成2:1的两部分,且经过点解: ⑴方法一:设方程为mx2+ny2=1(m>0,n>0,m≠n),将点的坐标方程,求出m=1/9,n=1/4。方法二:利用椭圆的几何性质,以坐标轴为对称轴的椭圆与坐标轴的交点就是椭圆的顶点,于是焦点在x轴上,且点P、Q分别是椭圆长轴与短轴的一个端点
,故a=3,b=2,所以椭圆的标准方程为 注:待定系数法求椭圆标准方程的步骤: ⑴定型; ⑵定量作业:P49 T51. 已知椭圆的一个焦点为F(6,0)点B,C是短轴的两端点,△FBC是等边三角形,求这个椭圆的标准方程。例4:(1)椭圆 的左焦点
是两个顶点,如果到F1直线AB的
距 离为 ,则椭圆的离心率e= .题型三:椭圆的离心率问题例4:(2)设M为椭圆 上一点, 为椭圆的焦点,
如果 ,求椭圆的离心率。练习:D2若椭圆两准线间的距离等于焦距的4倍,则这个椭圆的离心率是( )D2.2.2 椭圆的简单几何性质1-----点、直线与椭圆的位置关系2-----弦长公式(第三课时)探究点与椭圆有几种位置关系,该怎样判断呢?类比圆可以吗?点与椭圆的位置关系D练一下回忆:直线与圆的位置关系1.位置关系:相交、相切、相离
2.判别方法(代数法)
联立直线与椭圆的方程
消元得到二元一次方程组
(1)△>0?直线与圆相交?有两个公共点;
(2)△=0 ?直线与圆相切?有且只有一个公共点;
(3)△<0 ?直线与圆相离?无公共点.通法3.几何法点线距d与半径r的大小关系直线与椭圆的位置关系种类:相离(没有交点)相切(一个交点)相交(二个交点)相离(没有交点)
相切(一个交点)
相交(二个交点) 直线与椭圆的位置关系的判定代数方法1.位置关系:相交、相切、相离
2.判别方法(代数法)
联立直线与椭圆的方程
消元得到二元一次方程组
(1)△>0?直线与椭圆相交?有两个公共点;
(2)△=0 ?直线与椭圆相切?有且只有一个公共点;
(3)△<0 ?直线与椭圆相离?无公共点.通法1.直线与椭圆的位置关系例1.k为何值时,直线y=kx+2和曲线2x2+3y2=6有两个公共点?有一个公共点?没有公共点?1.直线与椭圆的位置关系 B 2.无论k为何值,直线y=kx+2和曲线
交点情况满足( )
A.没有公共点 B.一个公共点
C.两个公共点 D.有公共点变式: D 思考:最大的距离是多少?1.直线与椭圆的位置关系练习:已知直线y=x- 与椭圆x2+4y2=2 ,判断它们的位置关系.解:联立方程组消去y?>0因为所以,方程(1)有两个根,那么,相交所得的弦的弦长是多少?则原方程组有两组解….----- (1)1.直线与椭圆的位置关系设直线与椭圆交于P1(x1,y1),P2(x2,y2)两点,直线P1P2的斜率为k.弦长公式:2.弦长公式
例3.已知斜率为1的直线l过椭圆 的右焦点,
交椭圆于A,B两点,求弦AB之长.2.弦长公式例 4.已知椭圆 过点P(2,1)引一弦,使弦在这点被平分,求此弦所在直线的方程.解:韦达定理→斜率韦达定理法:利用韦达定理及中点坐标公式来构造弦中点问题点差法:利用端点在曲线上,坐标满足方程,作差构造
出中点坐标和斜率.点作差弦中点问题例 4.已知椭圆 过点P(2,1)引一弦,使弦在这点被平分,求此弦所在直线的方程.例4.已知椭圆 过点P(2,1)引一弦,使弦在这点被
平分,求此弦所在直线的方程.所以 x2+4y2=(4-x)2+4(2-y)2,整理得x+2y-4=0
从而A ,B在直线x+2y-4=0上
而过A,B两点的直线有且只有一条解后反思:中点弦问题求解关键在于充分利用“中点”这一 条件,灵活运用中点坐标公式及韦达定理,弦中点问题3、弦中点问题的两种处理方法:
(1)联立方程组,消去一个未知数,利用韦达定理;
(2)设两端点坐标,代入曲线方程相减可求出弦的斜率。 1、直线与椭圆的三种位置关系及判断方法;小 结
