2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.2.1双曲线及其标准方程课件(16张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.2.1双曲线及其标准方程课件(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 287.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 00:00:00 | ||
图片预览




文档简介
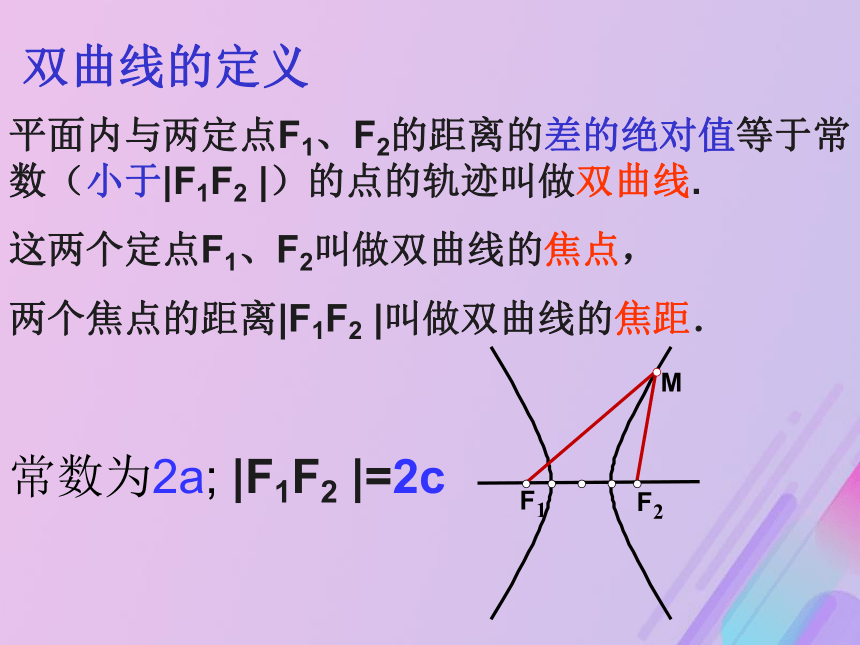
课件16张PPT。2.2.1 双曲线及其标准方程(第一课时)①若2a=0,则轨迹是线段F1F2的垂直平分线②若2a= ∣ F1F2 ∣,则轨迹是以F1、F2为端点
的两射线③若2a> ∣ F1F2 ∣,则轨迹不存在说明:平面内与两定点F1、F2的距离的差的绝对值等于常数(小于|F1F2 |)的点的轨迹叫做双曲线.
这两个定点F1、F2叫做双曲线的焦点,
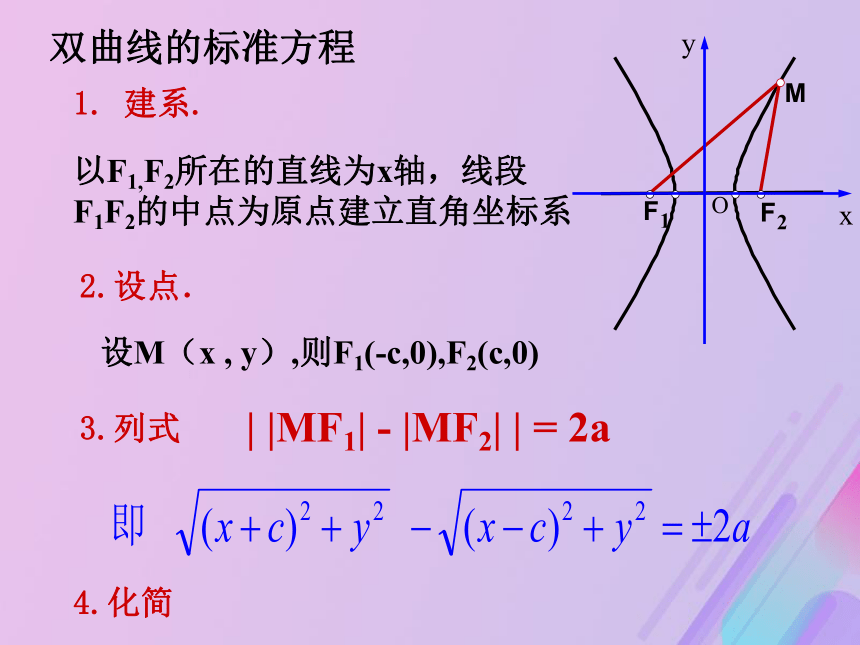
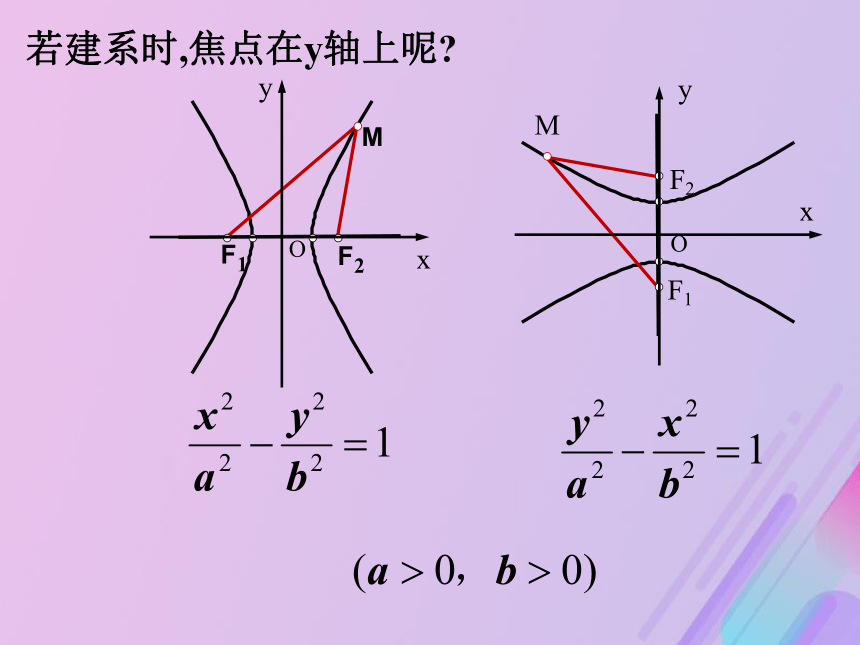
两个焦点的距离|F1F2 |叫做双曲线的焦距.双曲线的定义常数为2a; |F1F2 |=2c想一想如何求双曲线的方程?双曲线的标准方程1. 建系.以F1,F2所在的直线为x轴,线段F1F2的中点为原点建立直角坐标系2.设点.设M(x , y),则F1(-c,0),F2(c,0)3.列式4.化简 | |MF1| - |MF2| | = 2a此即为焦点在x轴上的双曲线的标准方程若建系时,焦点在y轴上呢?双曲线的标准方程问题:如何判断双曲线的焦点在哪个轴上?(二次项系数为正,焦点在相应的轴上)F(±c,0)F(±c,0)a>0,b>0,但a不一定大于b,c2=a2+b2a>b>0,a2=b2+c2双曲线与椭圆之间的区别与联系||MF1|-|MF2||=2a |MF1|+|MF2|=2a F(0,±c)F(0,±c)数学思想方法类比
数形结合
分类讨论
化归
的两射线③若2a> ∣ F1F2 ∣,则轨迹不存在说明:平面内与两定点F1、F2的距离的差的绝对值等于常数(小于|F1F2 |)的点的轨迹叫做双曲线.
这两个定点F1、F2叫做双曲线的焦点,
两个焦点的距离|F1F2 |叫做双曲线的焦距.双曲线的定义常数为2a; |F1F2 |=2c想一想如何求双曲线的方程?双曲线的标准方程1. 建系.以F1,F2所在的直线为x轴,线段F1F2的中点为原点建立直角坐标系2.设点.设M(x , y),则F1(-c,0),F2(c,0)3.列式4.化简 | |MF1| - |MF2| | = 2a此即为焦点在x轴上的双曲线的标准方程若建系时,焦点在y轴上呢?双曲线的标准方程问题:如何判断双曲线的焦点在哪个轴上?(二次项系数为正,焦点在相应的轴上)F(±c,0)F(±c,0)a>0,b>0,但a不一定大于b,c2=a2+b2a>b>0,a2=b2+c2双曲线与椭圆之间的区别与联系||MF1|-|MF2||=2a |MF1|+|MF2|=2a F(0,±c)F(0,±c)数学思想方法类比
数形结合
分类讨论
化归
