2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.3.1利用导数判断函数的单调性课件(20张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.3.1利用导数判断函数的单调性课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 10:15:09 | ||
图片预览








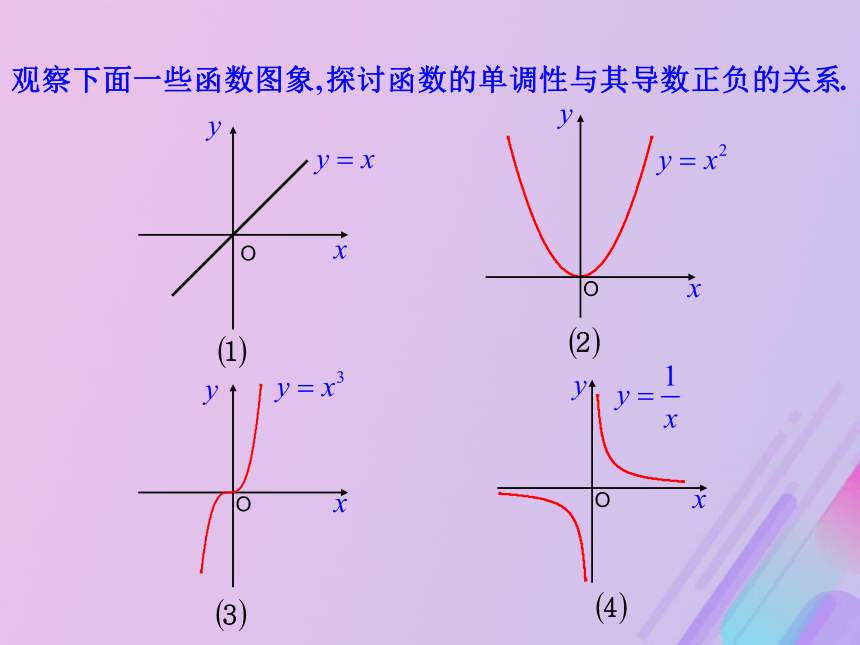
文档简介
课件20张PPT。一、情境设置: 过山车是一项富有刺激性的娱乐项目。那种风驰电掣、有惊无险的快感令不少年轻人着迷。 二、函数单调性定义 一般地,设函数 y = f (x) 的定义域为I :
如果对于定义域I内某个区间D上的任意两个自变量
的值 ,当 时,都有 ,
那么就说函数 f (x) 在区间D上是增函数.如果对于定义域I内某个区间D上的任意两个自变量的值 ,当 时,都有 ,那么就说函数 f (x) 在区间D上是减函数.三、导数的几何意义是什么?
3.3.1函数的单调性与导数(1)1.知识目标 : 使学生了解可导函数的单调性与其导数的关系,掌握如何利用导数的正负判断函数的单调区间和证明函数的单调性,提高学习导数和应用导数的意识.
2.能力目标 :使学生提高用新知识解决复杂函数单调性的能力,培养学生数形结合的思想.
3.情感与价值目标:培养学生用普遍联系的观点看待事物,加强师生间的交流,感受数学内容的统一性. 如图(1)表示高台跳水运动
员的高度 h 随时间 t 变化的
函数 的图象, 图(2)表示高台跳水
运动员的速度 v 随时间 t 变
化的函数 的图象.运动员从起跳到最高
点, 以及从最高点到入水这两
段时间的运动状态有什么区别?aabbttvhOO(1)(2)探究点:函数的单调性与其导函数的关系(1)(2)aabbttvhOO①运动员从起跳到最高点,离水面的高度h随时间t 的增
加而增加,即h(t)是增函数.相应地,②从最高点到入水,运动员离水面的高度h随时间t的增加而减少,即h(t)是减函数.相应地,(1)(2)提示:思考:这种情况是否具有一般性?例1 已知导函数 的下列信息:当1 < x < 4 时,当 x > 4或 x < 1时,当 x = 4或 x = 1时,试画出函数 的图象的大致形状. 当 x > 4 或 x < 1时, 可知 在此区间内单调递减;y=f(x)
随堂练习:1.确定函数f(x)=x2-2x+4在哪个区间内是增函数,哪个区间内是减函数.解:f′(x)=(x2-2x+4)′=2x-2.令2x-2>0,解得x>1.∴当x∈(1,+∞)时,f ’(x)>0,
f(x)是增函数.令2x-2<0,解得x<1.∴当x∈(-∞,1)时,f ’(x)<0,
f(x)是减函数.根据导数确定函数的单调性步骤:1.求出函数的导数.2.解不等式f′(x)>0,得函数单调递增区间;
解不等式f′(x)<0,得函数单调递减区间.【提升总结】【沙场点兵】
(2016·吉安高二检测)函数y=f(x)在定义域 内可
导,其图象如图所示,记y=f(x)的导函数为y=f′(x),则
不等式f′(x)≤0的解集为 .【解析】由题意不等式f′(x)≤0的解集
即函数y=f(x)的递减区间为 [2,3).
答案: [2,3)
通过这节课的学习,我们学到了什么? 不积跬步,无以至千里;
不积小流,无以成江海。 — 荀子谢谢大家!谢谢大家!
如果对于定义域I内某个区间D上的任意两个自变量
的值 ,当 时,都有 ,
那么就说函数 f (x) 在区间D上是增函数.如果对于定义域I内某个区间D上的任意两个自变量的值 ,当 时,都有 ,那么就说函数 f (x) 在区间D上是减函数.三、导数的几何意义是什么?
3.3.1函数的单调性与导数(1)1.知识目标 : 使学生了解可导函数的单调性与其导数的关系,掌握如何利用导数的正负判断函数的单调区间和证明函数的单调性,提高学习导数和应用导数的意识.
2.能力目标 :使学生提高用新知识解决复杂函数单调性的能力,培养学生数形结合的思想.
3.情感与价值目标:培养学生用普遍联系的观点看待事物,加强师生间的交流,感受数学内容的统一性. 如图(1)表示高台跳水运动
员的高度 h 随时间 t 变化的
函数 的图象, 图(2)表示高台跳水
运动员的速度 v 随时间 t 变
化的函数 的图象.运动员从起跳到最高
点, 以及从最高点到入水这两
段时间的运动状态有什么区别?aabbttvhOO(1)(2)探究点:函数的单调性与其导函数的关系(1)(2)aabbttvhOO①运动员从起跳到最高点,离水面的高度h随时间t 的增
加而增加,即h(t)是增函数.相应地,②从最高点到入水,运动员离水面的高度h随时间t的增加而减少,即h(t)是减函数.相应地,(1)(2)提示:思考:这种情况是否具有一般性?例1 已知导函数 的下列信息:当1 < x < 4 时,当 x > 4或 x < 1时,当 x = 4或 x = 1时,试画出函数 的图象的大致形状. 当 x > 4 或 x < 1时, 可知 在此区间内单调递减;y=f(x)
随堂练习:1.确定函数f(x)=x2-2x+4在哪个区间内是增函数,哪个区间内是减函数.解:f′(x)=(x2-2x+4)′=2x-2.令2x-2>0,解得x>1.∴当x∈(1,+∞)时,f ’(x)>0,
f(x)是增函数.令2x-2<0,解得x<1.∴当x∈(-∞,1)时,f ’(x)<0,
f(x)是减函数.根据导数确定函数的单调性步骤:1.求出函数的导数.2.解不等式f′(x)>0,得函数单调递增区间;
解不等式f′(x)<0,得函数单调递减区间.【提升总结】【沙场点兵】
(2016·吉安高二检测)函数y=f(x)在定义域 内可
导,其图象如图所示,记y=f(x)的导函数为y=f′(x),则
不等式f′(x)≤0的解集为 .【解析】由题意不等式f′(x)≤0的解集
即函数y=f(x)的递减区间为 [2,3).
答案: [2,3)
通过这节课的学习,我们学到了什么? 不积跬步,无以至千里;
不积小流,无以成江海。 — 荀子谢谢大家!谢谢大家!
