2018年高中数学第二章圆锥曲线与方程2.1.1曲线与方程的概念课件4新人教B版选修2_1(15张)
文档属性
| 名称 | 2018年高中数学第二章圆锥曲线与方程2.1.1曲线与方程的概念课件4新人教B版选修2_1(15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 10:17:35 | ||
图片预览





文档简介
课件15张PPT。2.1.1 曲线与方程的概念我们的生活数字化北京位于北纬39°56′
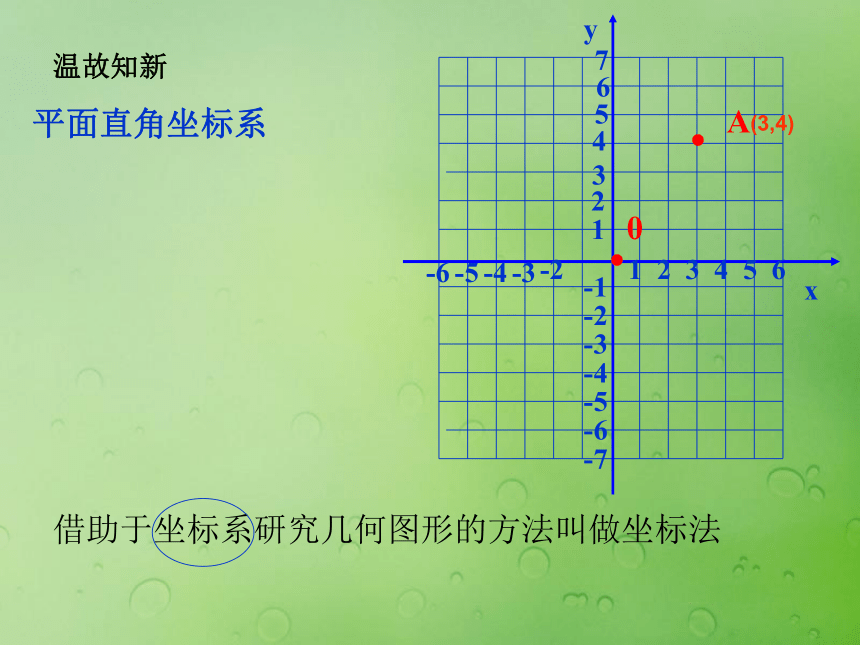
东经116°20′ 飞机的航线1 2 3 4 5 6-67654231-1-2-3-4-5-6-7-5-4-3-2yx..A0平面直角坐标系
借助于坐标系研究几何图形的方法叫做坐标法温故知新(3,4)
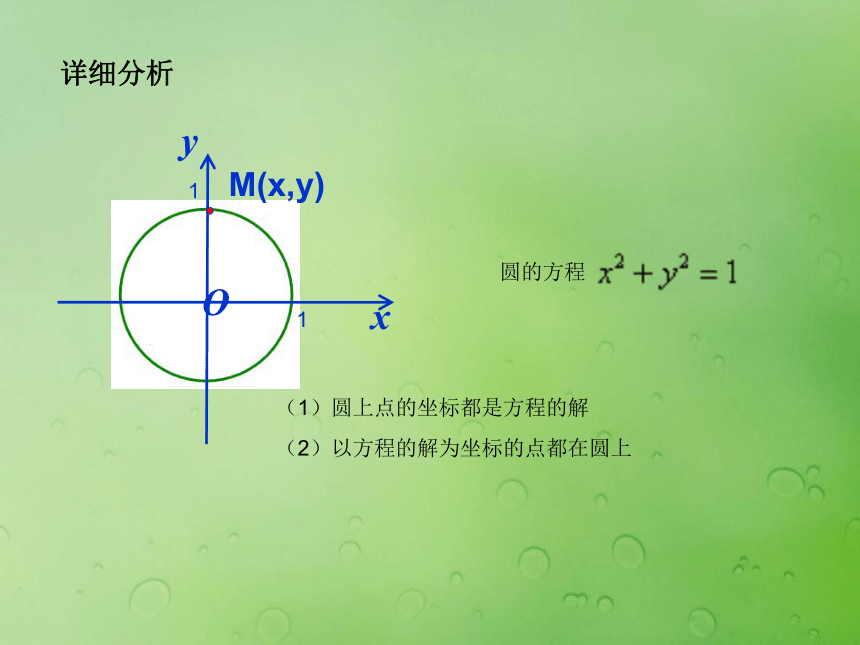
直线的方程 x-y=0 (1)直线上点的坐标都是方程x-y=0的解 (2)以方程x-y=0的解为坐标的点都在直线上.A(1,1).P(-3,1)复习引入那么这条直线叫做方程的直线,这个方程叫做直线的方程xOy11(1)圆上点的坐标都是方程的解(2)以方程的解为坐标的点都在圆上圆的方程详细分析M(x,y)一条曲线可以看成动点依某中条件运动的轨迹, 所以曲线的方程又称为满足某种条件的点的轨迹方程。 曲线与方程的概念一般地,在直角直角坐标系中,如果某曲线C上的点与一个二元方程 F(x, y)=0的实数解建立了如下的关系:
(1)曲线上的点的坐标都是这个方程 的解
(2)以这个方程的解为坐标的点都是曲线上的点
那么曲线C叫做方程的曲线;
方程F(x, y)=0叫做曲线的方程;总结归纳M(X,Y)∈CF(x, y)=0C= M(X,Y) ︱ F(x, y)=011例1 判断下列结论的对错,并说明理由。ⅰ 到两条坐标轴距离相等的点的轨迹方程是ⅰ 曲线与方程,
它们之间的关系符合(2)而不符合(1)ⅱ 圆心在原点,半径为1的圆的x轴上方及x轴上的点的轨迹方程是ⅱ 曲线与方程,
它们之间的关系符合(1)而不符合(2)11应用练习例2 求直线x-y=0与圆 的交点坐标。阅读课本34页巩固练习例2课堂小结①概念关系:方程的曲线,曲线的方程
②有关概念:坐标法,轨迹方程
③几何问题化为代数问题,以数助形的解析几何的思想例3 已知两圆
求证:对任意不等于-1的实数 ,方程
是通过两个已知圆交点的圆的方程。yx所以方程是通过两个已知圆交点的圆的方程0水下摄像机观测南澳一号沉船考古打捞 南澳一号是一艘沉没于汕头南澳海域的明代古船,船载万余件瓷器,自2010年4月初开始水下考古工作起,目前已经出水了大量文物。 教学目标★
请你先在纸上画出一条直线与一个圆,然后与你同桌同学所画的图形进行比较,你们所画的直线与圆位置关系一致吗? 同一坐标系(两轴上的单位长为1 cm)中画出直线的方程
圆的方程
yx1新课引入
东经116°20′ 飞机的航线1 2 3 4 5 6-67654231-1-2-3-4-5-6-7-5-4-3-2yx..A0平面直角坐标系
借助于坐标系研究几何图形的方法叫做坐标法温故知新(3,4)
直线的方程 x-y=0 (1)直线上点的坐标都是方程x-y=0的解 (2)以方程x-y=0的解为坐标的点都在直线上.A(1,1).P(-3,1)复习引入那么这条直线叫做方程的直线,这个方程叫做直线的方程xOy11(1)圆上点的坐标都是方程的解(2)以方程的解为坐标的点都在圆上圆的方程详细分析M(x,y)一条曲线可以看成动点依某中条件运动的轨迹, 所以曲线的方程又称为满足某种条件的点的轨迹方程。 曲线与方程的概念一般地,在直角直角坐标系中,如果某曲线C上的点与一个二元方程 F(x, y)=0的实数解建立了如下的关系:
(1)曲线上的点的坐标都是这个方程 的解
(2)以这个方程的解为坐标的点都是曲线上的点
那么曲线C叫做方程的曲线;
方程F(x, y)=0叫做曲线的方程;总结归纳M(X,Y)∈CF(x, y)=0C= M(X,Y) ︱ F(x, y)=011例1 判断下列结论的对错,并说明理由。ⅰ 到两条坐标轴距离相等的点的轨迹方程是ⅰ 曲线与方程,
它们之间的关系符合(2)而不符合(1)ⅱ 圆心在原点,半径为1的圆的x轴上方及x轴上的点的轨迹方程是ⅱ 曲线与方程,
它们之间的关系符合(1)而不符合(2)11应用练习例2 求直线x-y=0与圆 的交点坐标。阅读课本34页巩固练习例2课堂小结①概念关系:方程的曲线,曲线的方程
②有关概念:坐标法,轨迹方程
③几何问题化为代数问题,以数助形的解析几何的思想例3 已知两圆
求证:对任意不等于-1的实数 ,方程
是通过两个已知圆交点的圆的方程。yx所以方程是通过两个已知圆交点的圆的方程0水下摄像机观测南澳一号沉船考古打捞 南澳一号是一艘沉没于汕头南澳海域的明代古船,船载万余件瓷器,自2010年4月初开始水下考古工作起,目前已经出水了大量文物。 教学目标★
请你先在纸上画出一条直线与一个圆,然后与你同桌同学所画的图形进行比较,你们所画的直线与圆位置关系一致吗? 同一坐标系(两轴上的单位长为1 cm)中画出直线的方程
圆的方程
yx1新课引入
