2018年高中数学第二章圆锥曲线与方程2.2.1椭圆的标准方程课件5新人教B版选修2_1(22张)
文档属性
| 名称 | 2018年高中数学第二章圆锥曲线与方程2.2.1椭圆的标准方程课件5新人教B版选修2_1(22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 00:00:00 | ||
图片预览






文档简介
课件22张PPT。椭圆及其标准方程一:认识椭圆生活中的椭圆一:认识椭圆二:尝试探究、形成概念 取一条定长的细绳;
(1)若把它的两端用图钉固定在纸板上同一点处,用铅笔尖把绳子拉直,使笔尖在纸板上慢慢移动,画出的轨迹是一个圆。
(3)若绳子的两端拉开一段距离,再分别固定在纸板的两点处,用铅笔尖把绳子拉直,使笔尖在纸板上慢慢移动,画出的轨迹是什么曲线?动手实验(亲身体验)演示实验1圆的定义圆 平面内与一个定点的距离等于常数(大于0)的点的轨迹叫作圆.
这个定点叫做圆的圆心,
定长叫做圆的半径. 圆的定义:椭圆的定义:二:尝试探究、形成概念 类比 这两个定点叫做椭圆的焦点,
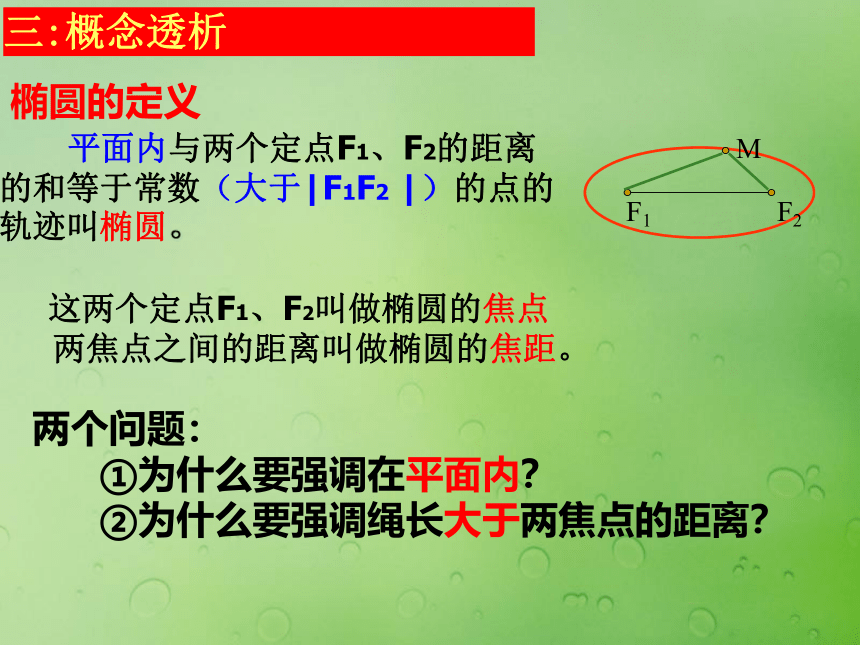
两焦点间的距离叫做椭圆的焦距. 平面内与两个定点F1、F2的距离的和等于常数(大于|F1F2 |)的点的轨迹叫椭圆。
这两个定点F1、F2叫做椭圆的焦点
两焦点之间的距离叫做椭圆的焦距。椭圆的定义两个问题:
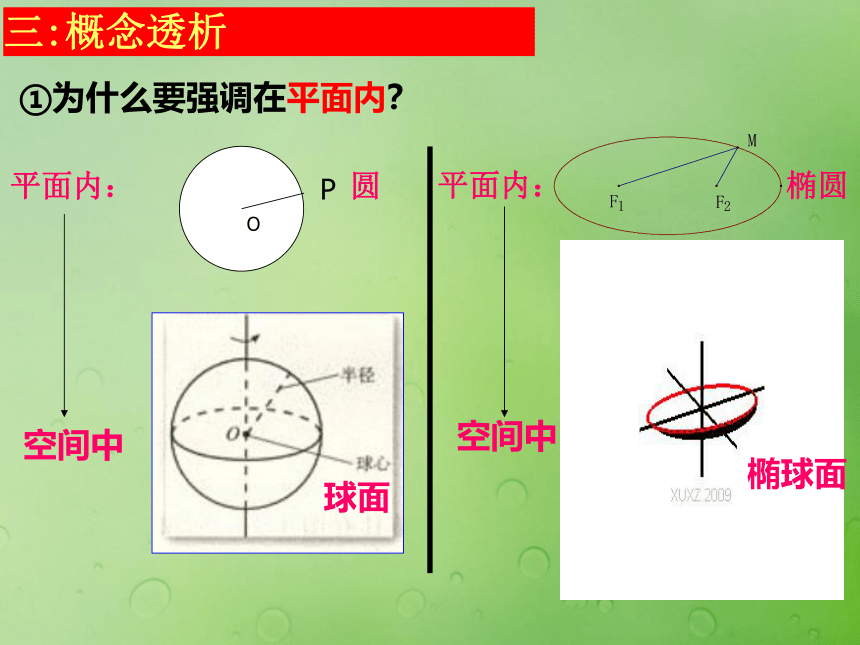
①为什么要强调在平面内?
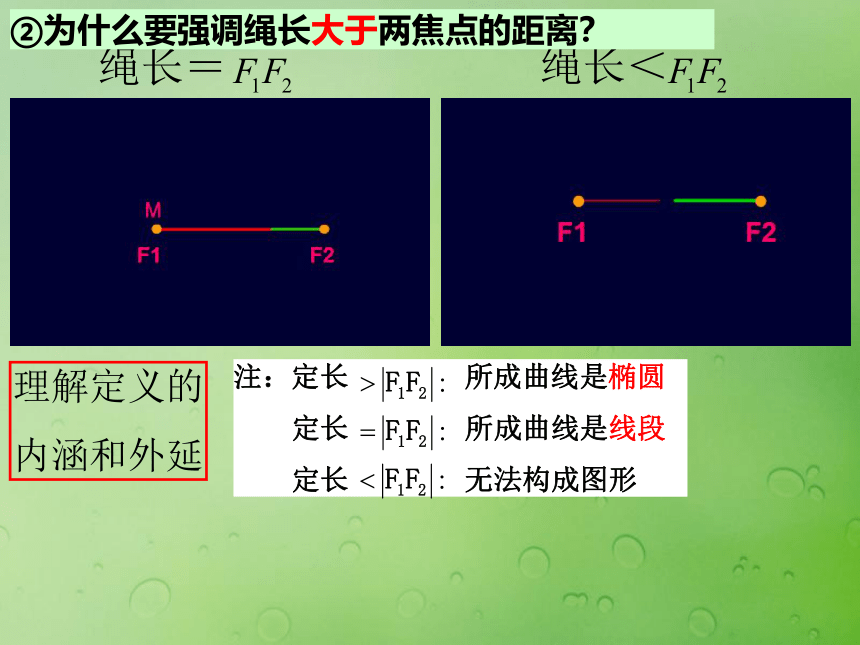
②为什么要强调绳长大于两焦点的距离?三:概念透析 平面内: 圆空间中空间中①为什么要强调在平面内?三:概念透析 ②为什么要强调绳长大于两焦点的距离?理解定义的
内涵和外延步骤一:建立直角坐标系;
步骤二:设动点坐标;
步骤三:限制条件,列方程;
步骤四:代入坐标
步骤五:化简方程。回顾:求曲线方程的步骤四:椭圆的标准方程的推导 (坐标法)? 探讨建立平面直角坐标系的方案建立平面直角坐标系通常遵循的原则:对称、“简洁”方案一解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图). 设M(x, y)是椭圆上任意一
点,椭圆的焦距2c(c>0),M
与F1和F2的距离的和等于正
常数2a (2a>2c) ,则F1、F2的坐标分别是(?c,0)、(c,0) .建构数学问题:上式如何化简呢?由椭圆的定义得,限制条件:代入坐标椭圆的标准方程的推导方案(1): 两边直接平方. (太繁琐)方案(2): 考虑两个根号下代数式的相似性这样化简可以减少平方次数,
而且为后面学习第二定义作了铺垫则 m +n= 2a ①化简得 数学中的
求美、求简 意识椭圆的标准方程椭圆的标准方程焦点在x上椭圆的标准方程(两种形式)方程特点(2)在椭圆两种标准方程中,总有a>b>0;(3)焦点在分母较大的变量所对应的坐标轴上;(1)方程的左边是两项平方和的形式,等号的右边是1;分母哪个大,焦点就在相应变量所对应的那个轴上a2-c2=b2(a>b>0)P={ M| |MF1 |+|MF2|=2a(2a>2c)}五:知识整理,形成系统(3)已知椭圆上一点 P到左焦点F1的距离等于6,
则点P到右焦点的距离是 ;
(4)若CD为过左焦点F1的弦,
则?CF1F2的周长为 ,
?F2CD的周长为 。 已知椭圆方程为 ,
则(1)a= , b= , c= ;
(2)焦点在 轴上,其焦点坐标为 ,
焦距为 。543(-3,0)、(3,0)6x41620变式一:将上题焦点改为(0,-4)、(0,4), 结果如何?变式二:将上题改为两个焦点的距离为8,椭圆上一点P到两焦点的
距离和等于10,结果如何?当焦点在X轴时,方程为:当焦点在Y轴时,方程为: 已知两个焦点的坐标分别是(-4,0)、(4,0),椭圆上一点P到两焦点距离的和等于10;k>0且k≠5/4 k>5/4 k=1/4 设F1(-3, 0)、F2(3, 0),且|MF1|+|MF2|=6,则点M的轨迹是 . 已知椭圆mx2+3y2-6m=0的一个焦点为(0, 2),求m的值.
(1)若把它的两端用图钉固定在纸板上同一点处,用铅笔尖把绳子拉直,使笔尖在纸板上慢慢移动,画出的轨迹是一个圆。
(3)若绳子的两端拉开一段距离,再分别固定在纸板的两点处,用铅笔尖把绳子拉直,使笔尖在纸板上慢慢移动,画出的轨迹是什么曲线?动手实验(亲身体验)演示实验1圆的定义圆 平面内与一个定点的距离等于常数(大于0)的点的轨迹叫作圆.
这个定点叫做圆的圆心,
定长叫做圆的半径. 圆的定义:椭圆的定义:二:尝试探究、形成概念 类比 这两个定点叫做椭圆的焦点,
两焦点间的距离叫做椭圆的焦距. 平面内与两个定点F1、F2的距离的和等于常数(大于|F1F2 |)的点的轨迹叫椭圆。
这两个定点F1、F2叫做椭圆的焦点
两焦点之间的距离叫做椭圆的焦距。椭圆的定义两个问题:
①为什么要强调在平面内?
②为什么要强调绳长大于两焦点的距离?三:概念透析 平面内: 圆空间中空间中①为什么要强调在平面内?三:概念透析 ②为什么要强调绳长大于两焦点的距离?理解定义的
内涵和外延步骤一:建立直角坐标系;
步骤二:设动点坐标;
步骤三:限制条件,列方程;
步骤四:代入坐标
步骤五:化简方程。回顾:求曲线方程的步骤四:椭圆的标准方程的推导 (坐标法)? 探讨建立平面直角坐标系的方案建立平面直角坐标系通常遵循的原则:对称、“简洁”方案一解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图). 设M(x, y)是椭圆上任意一
点,椭圆的焦距2c(c>0),M
与F1和F2的距离的和等于正
常数2a (2a>2c) ,则F1、F2的坐标分别是(?c,0)、(c,0) .建构数学问题:上式如何化简呢?由椭圆的定义得,限制条件:代入坐标椭圆的标准方程的推导方案(1): 两边直接平方. (太繁琐)方案(2): 考虑两个根号下代数式的相似性这样化简可以减少平方次数,
而且为后面学习第二定义作了铺垫则 m +n= 2a ①化简得 数学中的
求美、求简 意识椭圆的标准方程椭圆的标准方程焦点在x上椭圆的标准方程(两种形式)方程特点(2)在椭圆两种标准方程中,总有a>b>0;(3)焦点在分母较大的变量所对应的坐标轴上;(1)方程的左边是两项平方和的形式,等号的右边是1;分母哪个大,焦点就在相应变量所对应的那个轴上a2-c2=b2(a>b>0)P={ M| |MF1 |+|MF2|=2a(2a>2c)}五:知识整理,形成系统(3)已知椭圆上一点 P到左焦点F1的距离等于6,
则点P到右焦点的距离是 ;
(4)若CD为过左焦点F1的弦,
则?CF1F2的周长为 ,
?F2CD的周长为 。 已知椭圆方程为 ,
则(1)a= , b= , c= ;
(2)焦点在 轴上,其焦点坐标为 ,
焦距为 。543(-3,0)、(3,0)6x41620变式一:将上题焦点改为(0,-4)、(0,4), 结果如何?变式二:将上题改为两个焦点的距离为8,椭圆上一点P到两焦点的
距离和等于10,结果如何?当焦点在X轴时,方程为:当焦点在Y轴时,方程为: 已知两个焦点的坐标分别是(-4,0)、(4,0),椭圆上一点P到两焦点距离的和等于10;k>0且k≠5/4 k>5/4 k=1/4 设F1(-3, 0)、F2(3, 0),且|MF1|+|MF2|=6,则点M的轨迹是 . 已知椭圆mx2+3y2-6m=0的一个焦点为(0, 2),求m的值.
