2018年高中数学第三章空间向量与立体几何3.2.4二面角及其度量课件4新人教B版选修2_1(21张)
文档属性
| 名称 | 2018年高中数学第三章空间向量与立体几何3.2.4二面角及其度量课件4新人教B版选修2_1(21张) |  | |
| 格式 | zip | ||
| 文件大小 | 244.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 10:25:43 | ||
图片预览




文档简介
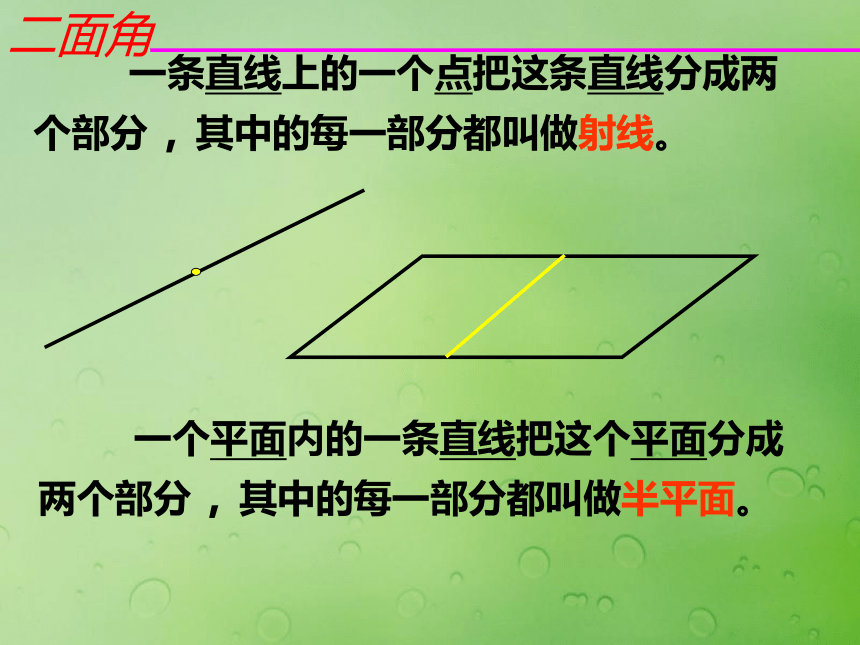
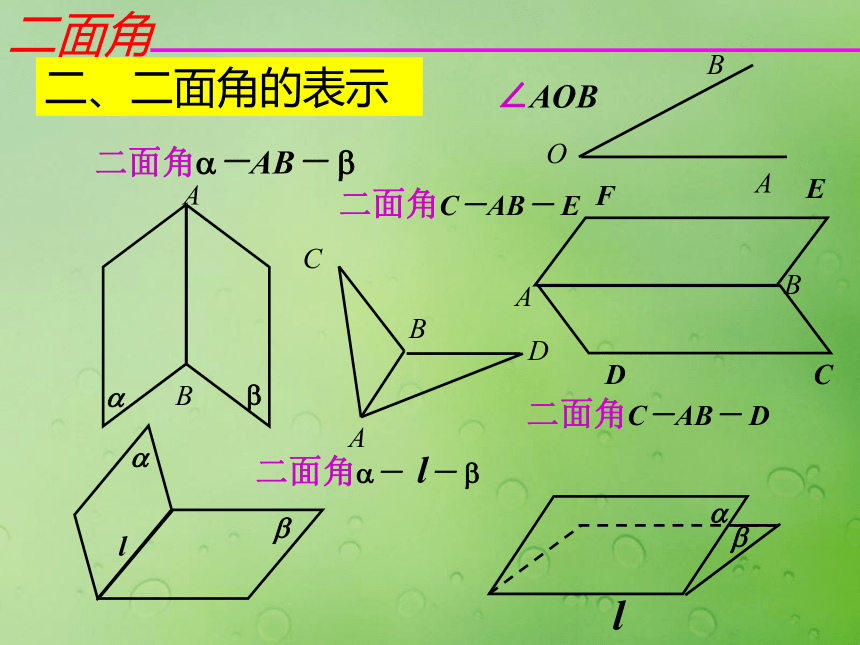
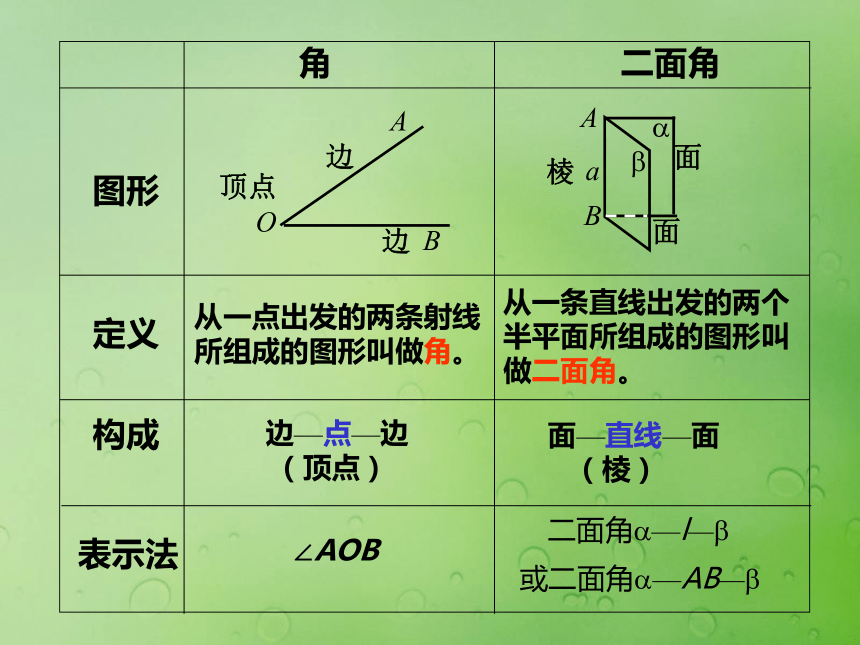
课件21张PPT。二面角二面角 一个平面内的一条直线把这个平面分成两个部分,其中的每一部分都叫做半平面。 一条直线上的一个点把这条直线分成两个部分,其中的每一部分都叫做射线。二面角 从一条直线出发的两个半平面所组成的图形叫做二面角。这条直线叫做二面角的棱。这两个半平面叫做二面角的面。一、二面角的定义二面角?-AB- ?二面角?- l- ?二面角C-AB- D∠AOB二、二面角的表示二面角C-AB- E从一点出发的两条射线所组成的图形叫做角。定义构成边—点—边
(顶点)表示法∠AOB从一条直线出发的两个半平面所组成的图形叫做二面角。面—直线—面
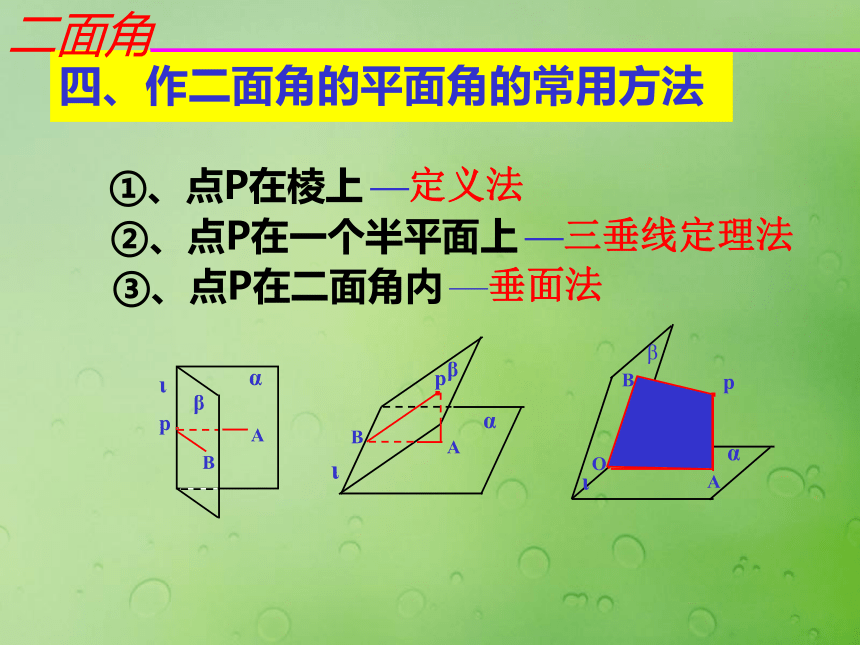
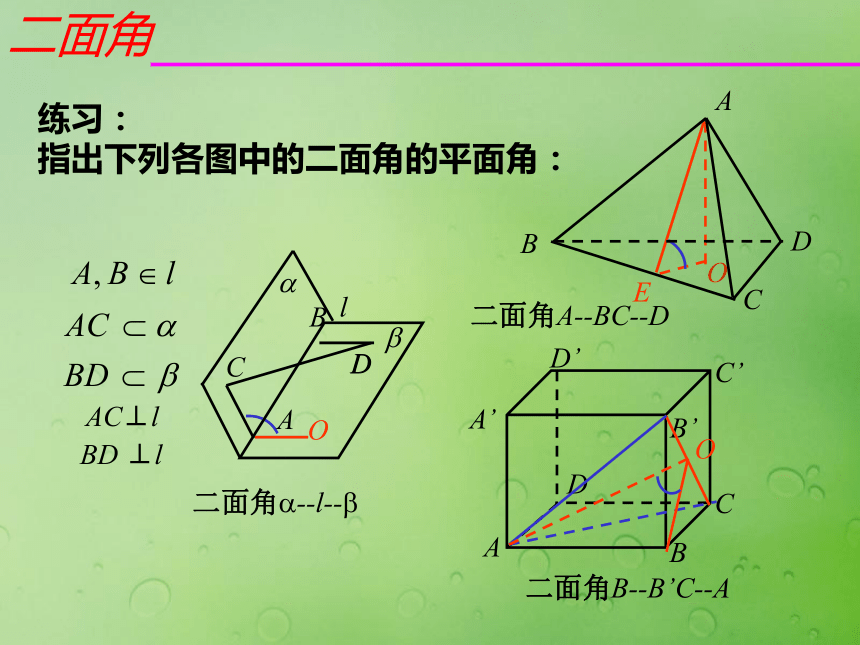
(棱)图形ABA1B1∠A O B∠A1O1B1 以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。平面角是直角的二面角叫做直二面角二面角的大小用它的平面角来度量三、二面角的平面角注意:二面角的平面角必须满足:3)角的边都要垂直于二面角的棱1)角的顶点在棱上2)角的两边分别在两个面内 以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。四、作二面角的平面角的常用方法①、点P在棱上②、点P在一个半平面上③、点P在二面角内ABABABO—定义法—三垂线定理法—垂面法二面角练习:
指出下列各图中的二面角的平面角:OEOO二面角如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上任一点,则二面角P-BC-A的平面角为:
A.∠ABP B.∠ACP C.都不是 练 习二面角AOD解:过 A作 AO⊥?于O,过 O作 OD⊥ l 于D,连AD则由三垂线定理得 AD⊥ l∵ AO为 A到?的距离 , AD为 A到 l 的距离∴∠ADO就是二面角 ?- l- ? 的平面角∵sin∠ADO= ∴ ∠ADO=60°∴二面角 ?- l- ? 的大小为60 °在Rt△ADO中,①②③五、二面角大小的计算:1、找到或作出二面角的平面角2、证明所作出的角就是所求的二面角的平面角3、计算出此角的大小一“作”二“证”三“计算”二面角作业回顾Sin( )=sin( )·sin( )线面角二面角线棱角例2.P为二面角α–ι–β内一点,PA⊥α,PB⊥β,且PA=5,PB=8,AB=7,
求这二面角的度数。 过PA、PB的平面PAB与
棱l 交于O点∵PA⊥α ∴PA⊥l ∵PB⊥β ∴PB⊥l ∴l⊥平面PAB∴∠AOB为二面角α–l–β的平面角又∵PA=5,PB=8,AB=7∴∠P= 60o ∴∠AOB=120o ∴这二面角的度数为120o解:例3.已知正方体ABCD-A1B1C1D1 ,M 、N 是棱B1C1, 、 C1D1之中点,求平面 MNDB与平面 B1BCC1所成二面角 的大小。分析:当两个半平面的图形的面积较容易计算,或二面角没有现成的棱时,可采用射影面积法,以避免繁杂的添线与计算。因此分别计算SBDNM和SBCC1M的面积,再用公式例4.如图,正方体ABCD-A1B1C1D1 中,E 为AA1 的中点,求二面角D1-DE-B 的大小。例 4 .已知A、B是120?的二面角?—l—?棱l上的两点,线段AC,BD分别在面?,?内,且AC⊥l,BD⊥l ,AC=2,BD=1,AB=3,求线段CD的长。O∠OAC =120?AO=BD=1, AC=2四边形ABDO为矩形, DO=AB=31.已知Rt△ABC在平面α内,斜边AB在30o的二面角α-AB-β的棱上,若AC=5,BC=12,求点C到平面β的距离CO。D2.在平面四边形ABCD中,AB=BC=2,AD=CD= , ∠B=120o;将三角形ABC沿四边形ABCD的对角线AC折起来,使DB′= ,求△AB′C所在平面与△ADC所在平面所成二面角的平面角的度数。ABCB’D二、二面角的平面角一、二面角的定义从空间一直线出发的两个半平面所组成的图形叫做二面角1、定义2、求二面角的平面角方法①点P在棱上②点P在一个半平面上③点P在二面角内ABABABO—定义法—三垂线定理法—垂面法二面角二面角二 面 角一、二面角的定义:二、二面角的表示方法:三、二面角的平面角:四、二面角的平面角的作法:五、二面角的计算:二 面 角 ?-AB- ?
二 面 角 C-AB- D
二 面 角 ?- l- ?1、根据定义作出来
2、利用直线和平面垂
直作出来
3、借助三垂线定理或
其逆定理作出来1、找到或作出二面角的平面角
2、证明 1中的角就是所求的 角
3、计算所求的角一“作”二“证”三“计算”从一条直线出发的两个半
平面所组成的图形叫做二
面角。这条直线叫做二面
角的棱。这两个半平面叫
做二面角的面。 221、二面角的平面角
必须满足三个条件
2、二面角的平面角
的大小与 其顶点
在棱上的位置无关
3、二面角的大小用
它的平面角的大
小来度量
(顶点)表示法∠AOB从一条直线出发的两个半平面所组成的图形叫做二面角。面—直线—面
(棱)图形ABA1B1∠A O B∠A1O1B1 以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。平面角是直角的二面角叫做直二面角二面角的大小用它的平面角来度量三、二面角的平面角注意:二面角的平面角必须满足:3)角的边都要垂直于二面角的棱1)角的顶点在棱上2)角的两边分别在两个面内 以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。四、作二面角的平面角的常用方法①、点P在棱上②、点P在一个半平面上③、点P在二面角内ABABABO—定义法—三垂线定理法—垂面法二面角练习:
指出下列各图中的二面角的平面角:OEOO二面角如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上任一点,则二面角P-BC-A的平面角为:
A.∠ABP B.∠ACP C.都不是 练 习二面角AOD解:过 A作 AO⊥?于O,过 O作 OD⊥ l 于D,连AD则由三垂线定理得 AD⊥ l∵ AO为 A到?的距离 , AD为 A到 l 的距离∴∠ADO就是二面角 ?- l- ? 的平面角∵sin∠ADO= ∴ ∠ADO=60°∴二面角 ?- l- ? 的大小为60 °在Rt△ADO中,①②③五、二面角大小的计算:1、找到或作出二面角的平面角2、证明所作出的角就是所求的二面角的平面角3、计算出此角的大小一“作”二“证”三“计算”二面角作业回顾Sin( )=sin( )·sin( )线面角二面角线棱角例2.P为二面角α–ι–β内一点,PA⊥α,PB⊥β,且PA=5,PB=8,AB=7,
求这二面角的度数。 过PA、PB的平面PAB与
棱l 交于O点∵PA⊥α ∴PA⊥l ∵PB⊥β ∴PB⊥l ∴l⊥平面PAB∴∠AOB为二面角α–l–β的平面角又∵PA=5,PB=8,AB=7∴∠P= 60o ∴∠AOB=120o ∴这二面角的度数为120o解:例3.已知正方体ABCD-A1B1C1D1 ,M 、N 是棱B1C1, 、 C1D1之中点,求平面 MNDB与平面 B1BCC1所成二面角 的大小。分析:当两个半平面的图形的面积较容易计算,或二面角没有现成的棱时,可采用射影面积法,以避免繁杂的添线与计算。因此分别计算SBDNM和SBCC1M的面积,再用公式例4.如图,正方体ABCD-A1B1C1D1 中,E 为AA1 的中点,求二面角D1-DE-B 的大小。例 4 .已知A、B是120?的二面角?—l—?棱l上的两点,线段AC,BD分别在面?,?内,且AC⊥l,BD⊥l ,AC=2,BD=1,AB=3,求线段CD的长。O∠OAC =120?AO=BD=1, AC=2四边形ABDO为矩形, DO=AB=31.已知Rt△ABC在平面α内,斜边AB在30o的二面角α-AB-β的棱上,若AC=5,BC=12,求点C到平面β的距离CO。D2.在平面四边形ABCD中,AB=BC=2,AD=CD= , ∠B=120o;将三角形ABC沿四边形ABCD的对角线AC折起来,使DB′= ,求△AB′C所在平面与△ADC所在平面所成二面角的平面角的度数。ABCB’D二、二面角的平面角一、二面角的定义从空间一直线出发的两个半平面所组成的图形叫做二面角1、定义2、求二面角的平面角方法①点P在棱上②点P在一个半平面上③点P在二面角内ABABABO—定义法—三垂线定理法—垂面法二面角二面角二 面 角一、二面角的定义:二、二面角的表示方法:三、二面角的平面角:四、二面角的平面角的作法:五、二面角的计算:二 面 角 ?-AB- ?
二 面 角 C-AB- D
二 面 角 ?- l- ?1、根据定义作出来
2、利用直线和平面垂
直作出来
3、借助三垂线定理或
其逆定理作出来1、找到或作出二面角的平面角
2、证明 1中的角就是所求的 角
3、计算所求的角一“作”二“证”三“计算”从一条直线出发的两个半
平面所组成的图形叫做二
面角。这条直线叫做二面
角的棱。这两个半平面叫
做二面角的面。 221、二面角的平面角
必须满足三个条件
2、二面角的平面角
的大小与 其顶点
在棱上的位置无关
3、二面角的大小用
它的平面角的大
小来度量
