24.3 正多边形和圆教案
图片预览



文档简介
九年级数学24.3《正多边形和圆》复习教案
【教学目标】
1.复习正多边形和圆的有关概念及对称性;
2.理解并掌握正多边形半径和边长、边心距、中心角之间的关系,会应用正多边形和圆的有关知识画正多边形;
3.会进行正多边形的有关计算.
【教学重难点】
正多边形半径和边长、边心距、中心角之间的关系
【教学过程】
要点梳理:
要点一、正多边形的概念
各边相等,各角也相等的多边形是正多边形.
要点诠释:
判断一个多边形是否是正多边形,必须满足两个条件:(1)各边相等;(2)各角相等;缺一不可.如菱形的各边都相等,矩形的各角都相等,但它们都不是正多边形(正方形是正多边形).
要点二、正多边形的重要元素
1.正多边形的外接圆和圆的内接正多边形
正多边形和圆的关系十分密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
2.正多边形的有关概念
(1)一个正多边形的外接圆的圆心叫做这个正多边形的中心.
(2)正多边形外接圆的半径叫做正多边形的半径.
(3)正多边形每一边所对的圆心角叫做正多边形的中心角.
(4)正多边形的中心到正多边形的一边的距离叫做正多边形的边心距.
3.正多边形的有关计算
(1)正n边形每一个内角的度数是;
(2)正n边形每个中心角的度数是;
(3)正n边形每个外角的度数是.
要点诠释:要熟悉正多边形的基本概念和基本图形,将待解决的问题转化为直角三角形.
要点三、正多边形的性质
1.正多边形都只有一个外接圆,圆有无数个内接正多边形.
2.正n边形的半径和边心距把正n边形分成2n个全等的直角三角形.
3.正多边形都是轴对称图形,对称轴的条数与它的边数相同,每条对称轴都通过正n边形的中心;当边数是偶数时,它也是中心对称图形,它的中心就是对称中心.
4.边数相同的正多边形相似。它们周长的比,边心距的比,半径的比都等于相似比,面积的比等于相似比的平方.
5.任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆
要点诠释:(1)各边相等的圆的内接多边形是圆的内接正多边形;(2)各角相等的圆的外切多边形是圆的外切正多边形.
要点四、正多边形的画法
1.用量角器等分圆
由于在同圆中相等的圆心角所对的弧也相等,因此作相等的圆心角(即等分顶点在圆心的周角)可以等分圆;根据同圆中相等弧所对的弦相等,依次连接各分点就可画出相应的正n边形.
2.用尺规等分圆
对于一些特殊的正n边形,可以用圆规和直尺作图.
①正四、八边形.
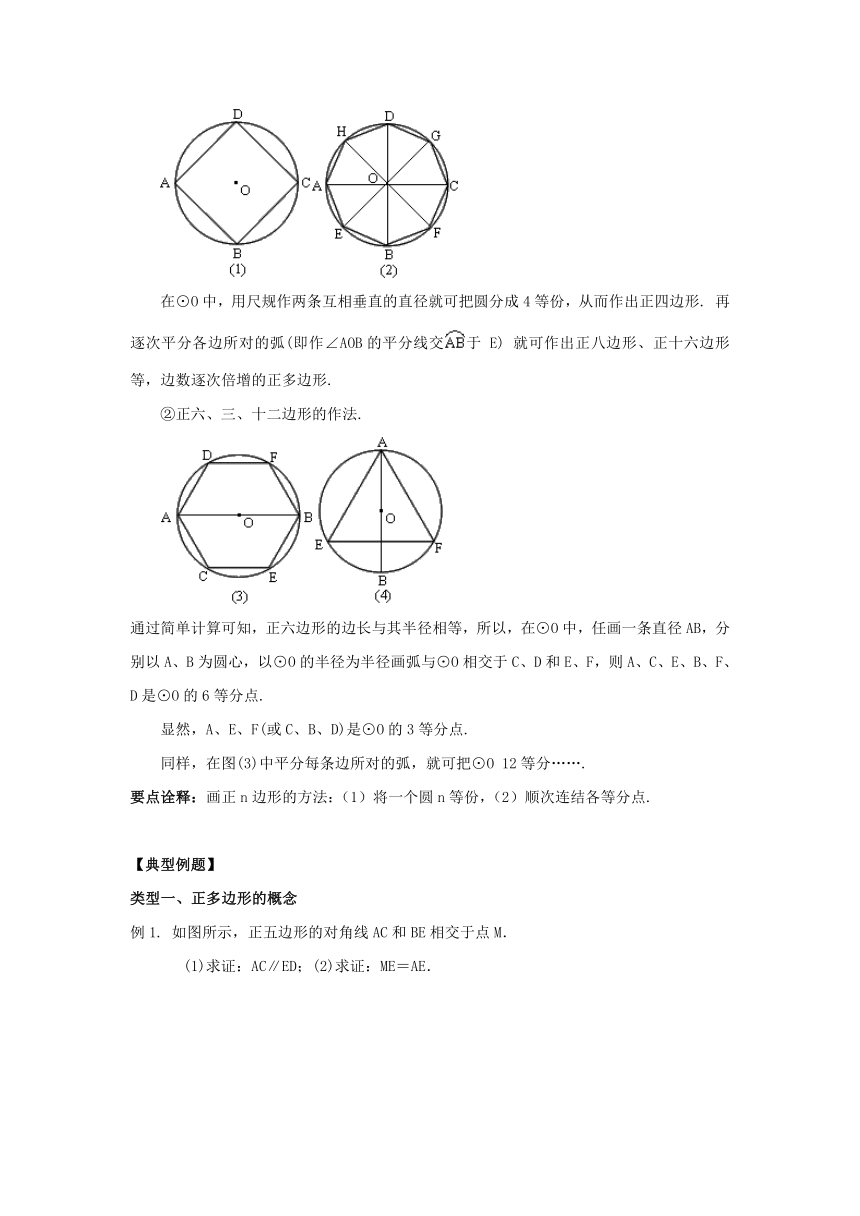
在⊙O中,用尺规作两条互相垂直的直径就可把圆分成4等份,从而作出正四边形. 再逐次平分各边所对的弧(即作∠AOB的平分线交于 E) 就可作出正八边形、正十六边形等,边数逐次倍增的正多边形.
②正六、三、十二边形的作法.
通过简单计算可知,正六边形的边长与其半径相等,所以,在⊙O中,任画一条直径AB,分别以A、B为圆心,以⊙O的半径为半径画弧与⊙O相交于C、D和E、F,则A、C、E、B、F、D是⊙O的6等分点.
显然,A、E、F(或C、B、D)是⊙O的3等分点.
同样,在图(3)中平分每条边所对的弧,就可把⊙O 12等分…….
要点诠释:画正n边形的方法:(1)将一个圆n等份,(2)顺次连结各等分点.
【典型例题】
类型一、正多边形的概念
例1. 如图所示,正五边形的对角线AC和BE相交于点M.
(1)求证:AC∥ED;(2)求证:ME=AE.
【解析与答案】
(1)正多边形必有外接圆,作出正五边形的外接⊙O,则的度数为,
∵ ∠EAC的度数等于的度数的一半,
∴ ∠EAC=,
同理,∠AED=×72°×3=108°,
∴ ∠EAC+∠AED=180°,
∴ ED∥AC.
(2)∵ ∠EMA=180-∠AEB-∠EAC=72°,
∴ ∠EAM=∠EMA=72°,
∴ EA=EM.
【点评】辅助圆是特殊的辅助线,一般用得很少,当有共圆条件时可作出辅助圆后利用圆的特殊性去解决直线型的问题.要证AC∥ED和ME=AE,都可用角的关系去证,而如果作出正五边形的外接圆,则用圆中角的关系去证比较容易.
例2.如图,正方形ABCD内接于⊙O,E为DC的中点,直线BE交⊙O于点F,若⊙O的半径为√2,则BF的长为 .
【答案】.
【解析】解:连接BD,DF,过点C作CN⊥BF于点F,
∵正方形ABCD内接于⊙O,⊙O的半径为√2,
∴BD=2√2,
∴AD=AB=BC=CD=2,
∵E为DC的中点,
∴CE=1,
∴BE=√5,
∴CN×BE=EC×BC,
∴CN×√5=2,
∴CN=2√5/5,
∴BN=4√5/5,
∴EN=BE﹣BN==√5/5,
∵BD为⊙O的直径,
∴∠BFD=90°,
∴△CEN≌△DEF,
∴EF=EN,
∴BF=BE+EF=6√5/5,
故答案为6√5/5.
【点评】此题主要考查了正多边形和圆以及勾股定理以及三角形面积等知识,根据圆周角定理得出正多边形边长是解题关键.
举一反三:
【变式】同一个圆的内接正六边形和外切正六边形的周长的比等于( )
A.3:4 B.:2 C.2: D.1:2
【答案】B;
【解析】设圆的半径为1,如图(1),连接OA、OB过O作OG⊥AB;
∵六边形ABCDE为正六边形,
∴∠AOB==60°;
∵OA=OB,OG⊥AB,
∴∠AOG==30°,
∴AG=OA?sin30°=1×0.5=0.5,(或由勾股定理求)
∴AB=2AG=2×0.5=1,
∴C六边形ABCD=6AB=6.
如图(2)连接OA、OB过O作OG⊥AB;
∵六边形ABCDE为正六边形,
∴∠AOB==60°,
∵OA=OB,OF⊥AB,
∴∠AOF==30°,
∴AG=OG?tan30°=,(或由勾股定理求)
∴AB=2AG=2×=,
∴C六边形ABCD=6AB=6×=4cm.
∴圆的内接正六边形和外切正六边形的周长的比=6:4=:2.
类型二、正多边形和圆的有关计算
例3.如图,AG是正八边形ABCDEFGH的一条对角线.
(1)在剩余的顶点B、C、D、E、F、H中,连接两个顶点,使连接的线段与AG平行,并说明理由;
(2)两边延长AB、CD、EF、GH,使延长线分别交于点P、Q、M、N,若AB=2,求四边形PQMN的面积.
【答案与解析】
解:(1)连接BF,则有BF∥AG.
理由如下:
∵ABCDEFGH是正八边形,
∴它的内角都为135°.
又∵HA=HG,
∴∠1=22.5°,
从而∠2=135°﹣∠1=112.5°.
由于正八边形ABCDEFGH关于直线BF对称,
即∠2+∠3=180°,故BF∥AG.
(2)根据题设可知∠PHA=∠PAH=45°,
∴∠P=90°,同理可得∠Q=∠M=90°,
∴四边形PQMN是矩形.
又∵∠PHA=∠PAH=∠QBC=∠QCB=∠MDE=∠MED=45°,AH=BC=DE,
∴△PAH≌△QCB≌△MDE,
∴PA=QB=QC=MD.即PQ=QM,
故四边形PQMN是正方形.
在Rt△PAH中,∵∠PAH=45°,AH=2,
∴PA=
∴.
【点评】此题主要考查了正多边形和圆以及全等三角形的判定与性质等知识,得出PQ的长是解题关键.
例4. 如图(1)所示,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G,求证:阴影部分四边形OFCG的面积是△ABC的面积的.
图(1)
【答案与解析】
(1)连OA、OB、OC,如图(2)所示,
图(2)
则OA=OB=OC,又AB=BC=CA.∴ △OAB≌△OBC≌△OCA,
又OD⊥BC于F,OE⊥AC于G,由垂径定理得AG=AC,FC=BC,
∴ AG=CF.∴ Rt△AOG≌Rt△COF
∴ .
【点评】首先连接OC,根据垂径定理的知识,易证得Rt△OCG≌Rt△OCF,设OG=a,根据直角三角形的性质与等边三角形的知识,即可求得阴影部分四边形OFCG的面积与△ABC的面积,继而求得答案.
举一反三:
【变式】如下图,若∠DOE保持120°角度不变,求证:当∠DOE绕着O点旋转时,由两条半径和△ABC的两条边围成的图形,图中阴影部分的面积始终是△ABC的面积的.
【答案】连接OA、OB、OC,由(1)知△OAB≌△OBC≌△OCA.
∴ ∠1=∠2.
设OD交BC于F,OE交AC于G,则∠AOC=∠3+∠4=120°,
∠DOE=∠5+∠4=120°,∴ ∠3=∠5.
在△OAG和△OCF中,∴ △OAG≌△OCF.
∴ .
课堂小结:正多边形的有关概念、正多边形半径和边长、边心距、中心角之间的关系
作业:导学案
【教学目标】
1.复习正多边形和圆的有关概念及对称性;
2.理解并掌握正多边形半径和边长、边心距、中心角之间的关系,会应用正多边形和圆的有关知识画正多边形;
3.会进行正多边形的有关计算.
【教学重难点】
正多边形半径和边长、边心距、中心角之间的关系
【教学过程】
要点梳理:
要点一、正多边形的概念
各边相等,各角也相等的多边形是正多边形.
要点诠释:
判断一个多边形是否是正多边形,必须满足两个条件:(1)各边相等;(2)各角相等;缺一不可.如菱形的各边都相等,矩形的各角都相等,但它们都不是正多边形(正方形是正多边形).
要点二、正多边形的重要元素
1.正多边形的外接圆和圆的内接正多边形
正多边形和圆的关系十分密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
2.正多边形的有关概念
(1)一个正多边形的外接圆的圆心叫做这个正多边形的中心.
(2)正多边形外接圆的半径叫做正多边形的半径.
(3)正多边形每一边所对的圆心角叫做正多边形的中心角.
(4)正多边形的中心到正多边形的一边的距离叫做正多边形的边心距.
3.正多边形的有关计算
(1)正n边形每一个内角的度数是;
(2)正n边形每个中心角的度数是;
(3)正n边形每个外角的度数是.
要点诠释:要熟悉正多边形的基本概念和基本图形,将待解决的问题转化为直角三角形.
要点三、正多边形的性质
1.正多边形都只有一个外接圆,圆有无数个内接正多边形.
2.正n边形的半径和边心距把正n边形分成2n个全等的直角三角形.
3.正多边形都是轴对称图形,对称轴的条数与它的边数相同,每条对称轴都通过正n边形的中心;当边数是偶数时,它也是中心对称图形,它的中心就是对称中心.
4.边数相同的正多边形相似。它们周长的比,边心距的比,半径的比都等于相似比,面积的比等于相似比的平方.
5.任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆
要点诠释:(1)各边相等的圆的内接多边形是圆的内接正多边形;(2)各角相等的圆的外切多边形是圆的外切正多边形.
要点四、正多边形的画法
1.用量角器等分圆
由于在同圆中相等的圆心角所对的弧也相等,因此作相等的圆心角(即等分顶点在圆心的周角)可以等分圆;根据同圆中相等弧所对的弦相等,依次连接各分点就可画出相应的正n边形.
2.用尺规等分圆
对于一些特殊的正n边形,可以用圆规和直尺作图.
①正四、八边形.
在⊙O中,用尺规作两条互相垂直的直径就可把圆分成4等份,从而作出正四边形. 再逐次平分各边所对的弧(即作∠AOB的平分线交于 E) 就可作出正八边形、正十六边形等,边数逐次倍增的正多边形.
②正六、三、十二边形的作法.
通过简单计算可知,正六边形的边长与其半径相等,所以,在⊙O中,任画一条直径AB,分别以A、B为圆心,以⊙O的半径为半径画弧与⊙O相交于C、D和E、F,则A、C、E、B、F、D是⊙O的6等分点.
显然,A、E、F(或C、B、D)是⊙O的3等分点.
同样,在图(3)中平分每条边所对的弧,就可把⊙O 12等分…….
要点诠释:画正n边形的方法:(1)将一个圆n等份,(2)顺次连结各等分点.
【典型例题】
类型一、正多边形的概念
例1. 如图所示,正五边形的对角线AC和BE相交于点M.
(1)求证:AC∥ED;(2)求证:ME=AE.
【解析与答案】
(1)正多边形必有外接圆,作出正五边形的外接⊙O,则的度数为,
∵ ∠EAC的度数等于的度数的一半,
∴ ∠EAC=,
同理,∠AED=×72°×3=108°,
∴ ∠EAC+∠AED=180°,
∴ ED∥AC.
(2)∵ ∠EMA=180-∠AEB-∠EAC=72°,
∴ ∠EAM=∠EMA=72°,
∴ EA=EM.
【点评】辅助圆是特殊的辅助线,一般用得很少,当有共圆条件时可作出辅助圆后利用圆的特殊性去解决直线型的问题.要证AC∥ED和ME=AE,都可用角的关系去证,而如果作出正五边形的外接圆,则用圆中角的关系去证比较容易.
例2.如图,正方形ABCD内接于⊙O,E为DC的中点,直线BE交⊙O于点F,若⊙O的半径为√2,则BF的长为 .
【答案】.
【解析】解:连接BD,DF,过点C作CN⊥BF于点F,
∵正方形ABCD内接于⊙O,⊙O的半径为√2,
∴BD=2√2,
∴AD=AB=BC=CD=2,
∵E为DC的中点,
∴CE=1,
∴BE=√5,
∴CN×BE=EC×BC,
∴CN×√5=2,
∴CN=2√5/5,
∴BN=4√5/5,
∴EN=BE﹣BN==√5/5,
∵BD为⊙O的直径,
∴∠BFD=90°,
∴△CEN≌△DEF,
∴EF=EN,
∴BF=BE+EF=6√5/5,
故答案为6√5/5.
【点评】此题主要考查了正多边形和圆以及勾股定理以及三角形面积等知识,根据圆周角定理得出正多边形边长是解题关键.
举一反三:
【变式】同一个圆的内接正六边形和外切正六边形的周长的比等于( )
A.3:4 B.:2 C.2: D.1:2
【答案】B;
【解析】设圆的半径为1,如图(1),连接OA、OB过O作OG⊥AB;
∵六边形ABCDE为正六边形,
∴∠AOB==60°;
∵OA=OB,OG⊥AB,
∴∠AOG==30°,
∴AG=OA?sin30°=1×0.5=0.5,(或由勾股定理求)
∴AB=2AG=2×0.5=1,
∴C六边形ABCD=6AB=6.
如图(2)连接OA、OB过O作OG⊥AB;
∵六边形ABCDE为正六边形,
∴∠AOB==60°,
∵OA=OB,OF⊥AB,
∴∠AOF==30°,
∴AG=OG?tan30°=,(或由勾股定理求)
∴AB=2AG=2×=,
∴C六边形ABCD=6AB=6×=4cm.
∴圆的内接正六边形和外切正六边形的周长的比=6:4=:2.
类型二、正多边形和圆的有关计算
例3.如图,AG是正八边形ABCDEFGH的一条对角线.
(1)在剩余的顶点B、C、D、E、F、H中,连接两个顶点,使连接的线段与AG平行,并说明理由;
(2)两边延长AB、CD、EF、GH,使延长线分别交于点P、Q、M、N,若AB=2,求四边形PQMN的面积.
【答案与解析】
解:(1)连接BF,则有BF∥AG.
理由如下:
∵ABCDEFGH是正八边形,
∴它的内角都为135°.
又∵HA=HG,
∴∠1=22.5°,
从而∠2=135°﹣∠1=112.5°.
由于正八边形ABCDEFGH关于直线BF对称,
即∠2+∠3=180°,故BF∥AG.
(2)根据题设可知∠PHA=∠PAH=45°,
∴∠P=90°,同理可得∠Q=∠M=90°,
∴四边形PQMN是矩形.
又∵∠PHA=∠PAH=∠QBC=∠QCB=∠MDE=∠MED=45°,AH=BC=DE,
∴△PAH≌△QCB≌△MDE,
∴PA=QB=QC=MD.即PQ=QM,
故四边形PQMN是正方形.
在Rt△PAH中,∵∠PAH=45°,AH=2,
∴PA=
∴.
【点评】此题主要考查了正多边形和圆以及全等三角形的判定与性质等知识,得出PQ的长是解题关键.
例4. 如图(1)所示,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G,求证:阴影部分四边形OFCG的面积是△ABC的面积的.
图(1)
【答案与解析】
(1)连OA、OB、OC,如图(2)所示,
图(2)
则OA=OB=OC,又AB=BC=CA.∴ △OAB≌△OBC≌△OCA,
又OD⊥BC于F,OE⊥AC于G,由垂径定理得AG=AC,FC=BC,
∴ AG=CF.∴ Rt△AOG≌Rt△COF
∴ .
【点评】首先连接OC,根据垂径定理的知识,易证得Rt△OCG≌Rt△OCF,设OG=a,根据直角三角形的性质与等边三角形的知识,即可求得阴影部分四边形OFCG的面积与△ABC的面积,继而求得答案.
举一反三:
【变式】如下图,若∠DOE保持120°角度不变,求证:当∠DOE绕着O点旋转时,由两条半径和△ABC的两条边围成的图形,图中阴影部分的面积始终是△ABC的面积的.
【答案】连接OA、OB、OC,由(1)知△OAB≌△OBC≌△OCA.
∴ ∠1=∠2.
设OD交BC于F,OE交AC于G,则∠AOC=∠3+∠4=120°,
∠DOE=∠5+∠4=120°,∴ ∠3=∠5.
在△OAG和△OCF中,∴ △OAG≌△OCF.
∴ .
课堂小结:正多边形的有关概念、正多边形半径和边长、边心距、中心角之间的关系
作业:导学案
同课章节目录
