24.3 正多边形和圆复习导学案
图片预览

文档简介
九年级数学24.3《正多边形和圆》复习导学案
【学习目标】
1.了解正多边形和圆的有关概念及对称性;
2.理解并掌握正多边形半径和边长、边心距、中心角之间的关系,会应用正多边形和圆的有关知识画正多边形;
3.会进行正多边形的有关计算.
【要点梳理】
要点一、正多边形的概念
各边相等,各角也相等的多边形是正多边形.
要点二、正多边形的重要元素
正多边形的外接圆和圆的内接正多边形
2.正多边形的有关概念
3.正多边形的有关计算
(1)正n边形每一个内角的度数是(N-2)180°/N;
(2)正n边形每个中心角的度数是360°/N;
(3)正n边形每个外角的度数是360°/N.
要点三、正多边形的性质
1.正多边形都只有一个外接圆,圆有无数个内接正多边形.
2.正n边形的半径和边心距把正n边形分成2n个全等的直角三角形.
3.正多边形都是轴对称图形,对称轴的条数与它的边数相同,每条对称轴都通过正n边形的中心;当边数是偶数时,它也是中心对称图形,它的中心就是对称中心.
4.边数相同的正多边形相似。它们周长的比,边心距的比,半径的比都等于相似比,面积的比等于相似比的平方.
5.任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆
要点四、正多边形的画法
1.用量角器等分圆
2.用尺规等分圆
【典型例题】
类型一、正多边形的概念
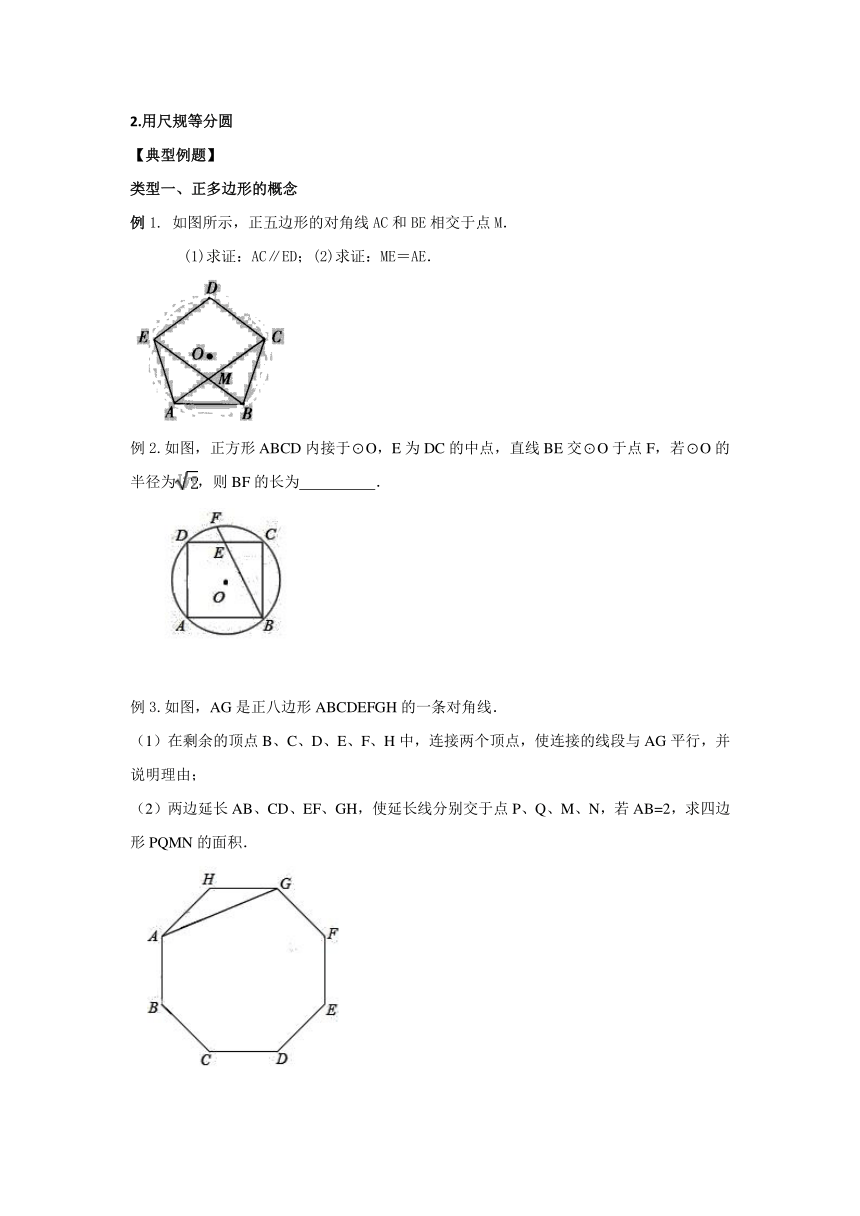
例1. 如图所示,正五边形的对角线AC和BE相交于点M.
(1)求证:AC∥ED;(2)求证:ME=AE.
例2.如图,正方形ABCD内接于⊙O,E为DC的中点,直线BE交⊙O于点F,若⊙O的半径为,则BF的长为 .
例3.如图,AG是正八边形ABCDEFGH的一条对角线.
(1)在剩余的顶点B、C、D、E、F、H中,连接两个顶点,使连接的线段与AG平行,并说明理由;
(2)两边延长AB、CD、EF、GH,使延长线分别交于点P、Q、M、N,若AB=2,求四边形PQMN的面积.
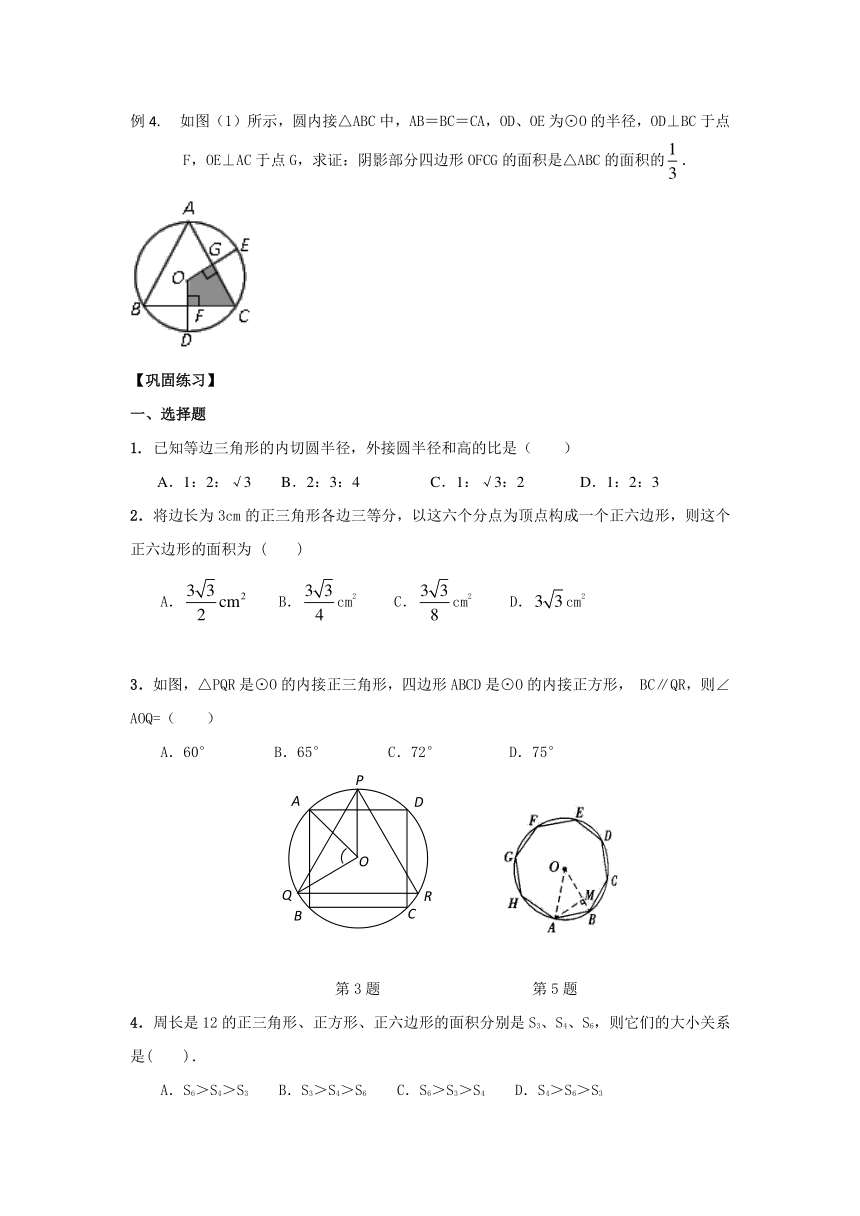
例4. 如图(1)所示,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G,求证:阴影部分四边形OFCG的面积是△ABC的面积的.
【巩固练习】
一、选择题
1. 已知等边三角形的内切圆半径,外接圆半径和高的比是( )
A.1:2:√3 B. 2:3:4 C. 1:√3:2 D. 1:2:3
2.将边长为3cm的正三角形各边三等分,以这六个分点为顶点构成一个正六边形,则这个正六边形的面积为 ( )
A. B.cm2 C.cm2 D.cm2
3.如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形, BC∥QR,则∠AOQ=( )
A.60° B.65° C.72° D.75°
第3题 第5题
4.周长是12的正三角形、正方形、正六边形的面积分别是S3、S4、S6,则它们的大小关系是( ).
A.S6>S4>S3 B.S3>S4>S6 C.S6>S3>S4 D.S4>S6>S3
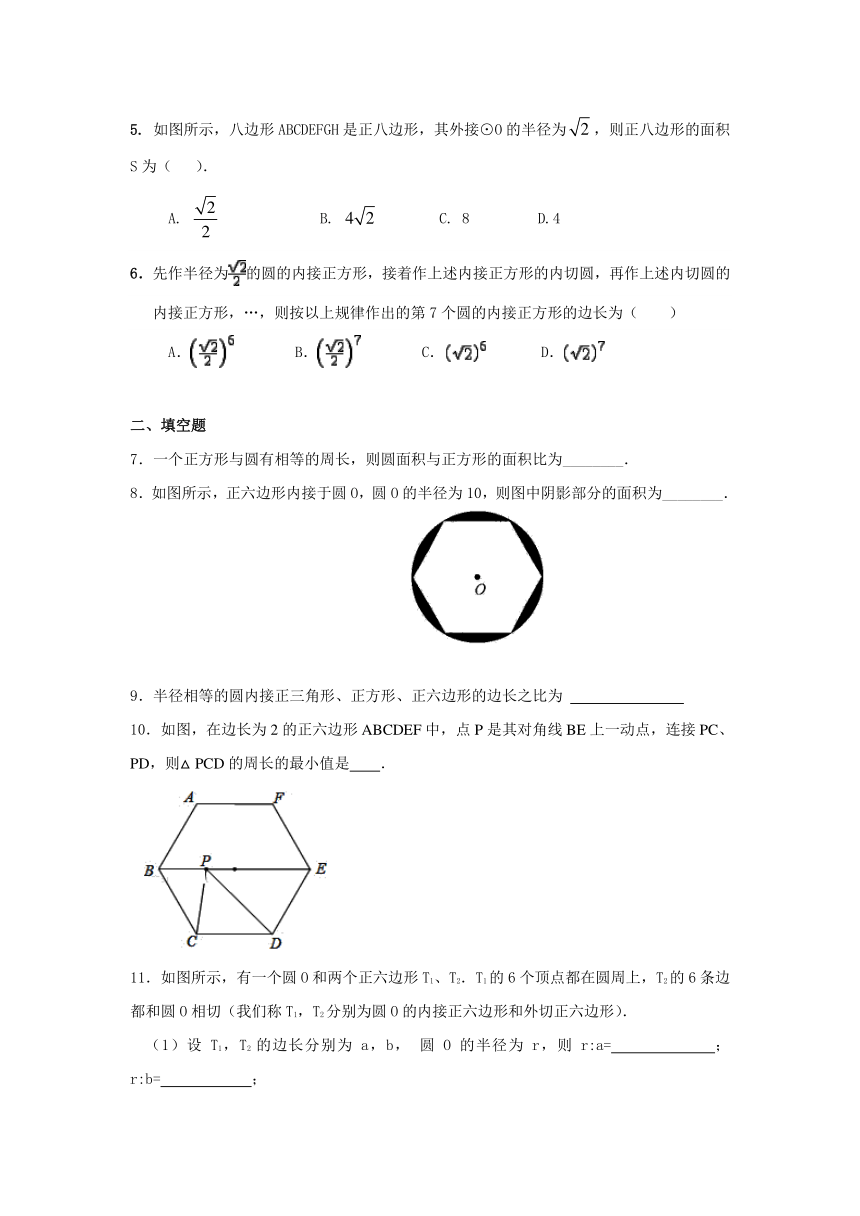
5. 如图所示,八边形ABCDEFGH是正八边形,其外接⊙O的半径为,则正八边形的面积S为( ).
A. B. C. 8 D.4
6.先作半径为的圆的内接正方形,接着作上述内接正方形的内切圆,再作上述内切圆的内接正方形,…,则按以上规律作出的第7个圆的内接正方形的边长为( )
A. B. C. D.
二、填空题
7.一个正方形与圆有相等的周长,则圆面积与正方形的面积比为________.
8.如图所示,正六边形内接于圆O,圆O的半径为10,则图中阴影部分的面积为________.
半径相等的圆内接正三角形、正方形、正六边形的边长之比为
10.如图,在边长为2的正六边形ABCDEF中,点P是其对角线BE上一动点,连接PC、PD,则△PCD的周长的最小值是 .
11.如图所示,有一个圆O和两个正六边形T1、T2.T1的6个顶点都在圆周上,T2的6条边都和圆O相切(我们称T1,T2分别为圆O的内接正六边形和外切正六边形).
(1)设T1,T2的边长分别为a,b, 圆O的半径为r,则r:a= ; r:b= ;
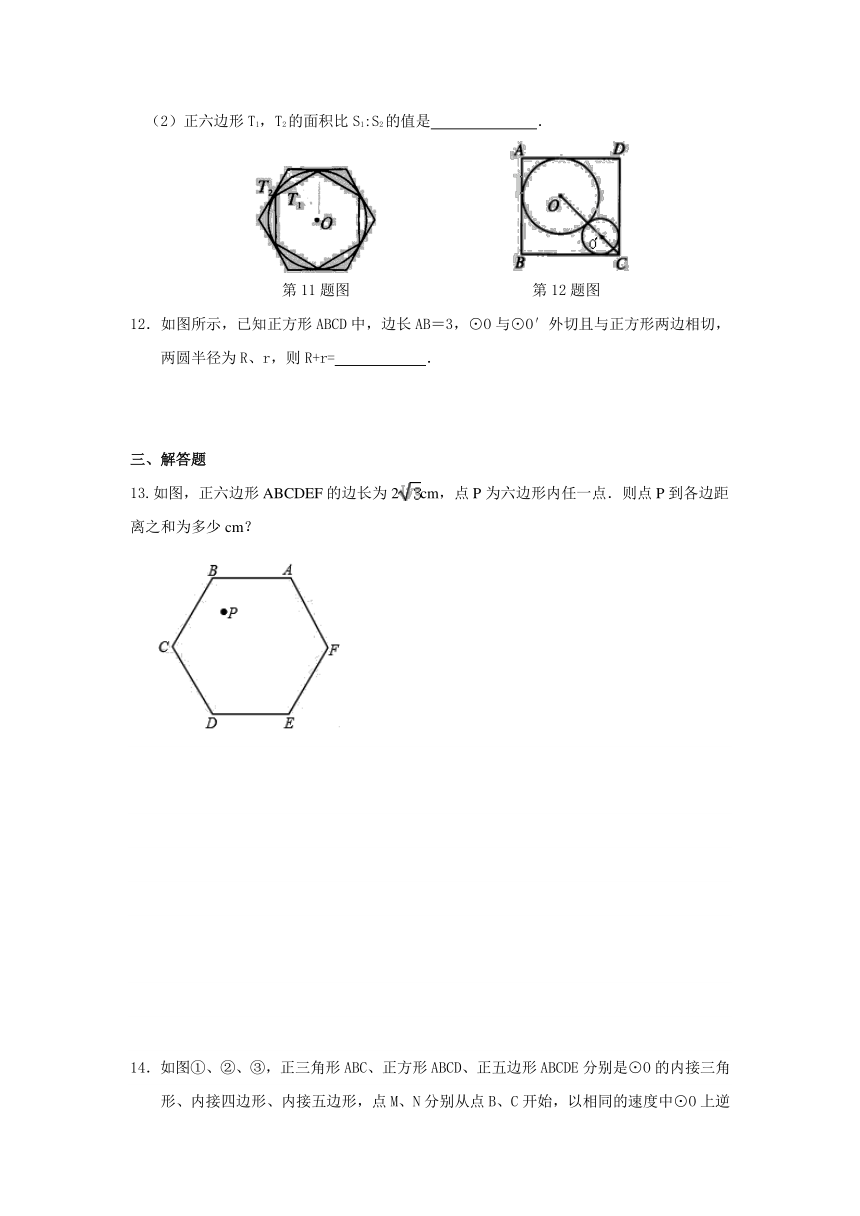
(2)正六边形T1,T2的面积比S1:S2的值是 .
第11题图 第12题图
12.如图所示,已知正方形ABCD中,边长AB=3,⊙O与⊙O′外切且与正方形两边相切,两圆半径为R、r,则R+r= .
三、解答题
13.如图,正六边形ABCDEF的边长为2cm,点P为六边形内任一点.则点P到各边距离之和为多少cm?
14.如图①、②、③,正三角形ABC、正方形ABCD、正五边形ABCDE分别是⊙O的内接三角形、内接四边形、内接五边形,点M、N分别从点B、C开始,以相同的速度中⊙O上逆时针运动.
(1)求图①中∠APB的度数;
(2)图②中,∠APB的度数是 ,图③中∠APB的度数是 ;
(3)根据前面探索,你能否将本题推广到一般的正n边形情况?若能,写出推广问题和结论;若不能,请说明理由.
15.如图,正三角形、正方形、正六边形等正n边形与圆的形状有差异,我们将正n边形与圆的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设正n边形的每个内角的度数为m°,将正n边形的“接近度”定义为|180-m|.于是,|180-m|越小,该正n边形就越接近于圆,
①若n=20,则该正n边形的“接近度”等于 ;
②当“接近度”等于 时,正n边形就成了圆.
(2)设一个正n边形的半径(即正n边形外接圆的半径)为R,边心距(即正n边形的中心到各边的距离)为r,将正n边形的“接近度”定义为|R-r|,于是|R-r|越小,正n边形就越接近于圆.你认为这种说法是否合理?若不合理,请给出正n边形“接近度”的一个合理定义.
【答案与解析】
一、选择题
1.【答案】D;
【解析】解:图中内切圆半径是OD,外接圆的半径是OC,高是AD,
因而AD=OC+OD;
在直角△OCD中,∠DOC=60°,
则OD:OC=1:2,
因而OD:OC:AD=1:2:3,
所以内切圆半径,外接圆半径和高的比是1:2:3.故选D.
2.【答案】A;
【解析】所得正六边形边长为1,∴ .
3.【答案】D;
【解析】易求∠POQ=120°,∠AOP=45°,则∠AOQ=∠POQ-∠AOP=120°-45°=75°.
4.【答案】A;
【解析】如图(1),∵ AB=4,AD=2,∠OAD=30°,∴ OD=.
∴ .
如图(2),∵ AB=AC=3,∴ S4=3×3=9.
如图(3),∵ CD=2,∴ OC=2,CM=1,
∴ OM=.
∴ .
又∵ ,
∴ ,故选A.
5.【答案】B;
【解析】连接OA、OB,过A作AM⊥OB于M,
∵ ,
∴ △AOM是等腰直角三角形.
又,∴ AM=1,
∴ ,
∴ ,
6.【答案】A.
【解析】由于圆内接正方形的边长与圆的半径的比为,内接正方形的内切圆的半径与正方形的边长的比为0.5,
即这样做一次后,圆的内接正方形的边长为×=1;
做第二次后的正方形的边长为;
依次类推可得:第n个正方形的边长是()n-1,
则做第7次后的圆的内接正方形的边长为.
故选A.
二、填空题
7.【答案】 ;
【解析】 设正方形边长为a,则周长为4a,面积为,圆周长也为4a,则,
∴ ,∴
∴ .
8.【答案】;
【解析】图中阴影部分面积等于圆的面积减去正六边形的面积.
∵ ,
,
∴
9.【答案】::1;
【解析】设圆的半径为R,
如图(一),连接OB,过O作OD⊥BC于D,
则∠OBC=30°,BD=OB?cos30°=R,(或由勾股定理求)
故BC=2BD=R;
如图(二),连接OB、OC,过O作OE⊥BC于E,
则△OBE是等腰直角三角形,
2BE2=OB2,即BE=,
故BC=R;
如图(三),连接OA、OB,过O作OG⊥AB,
则△OAB是等边三角形,
故AG=OA?cos60°=R,AB=2AG=R,(或由勾股定理求)
故圆内接正三角形、正方形、正六边形的边长之比为R:R:R=::1.
10.【答案】6.
【解析】要使△PCD的周长的最小,即PC+PD最小.
利用正多边形的性质可得点C关于BE的对称点为点A,连接AD交BE于点P',那么有P'C=P'A,P'C+P'D=AD最小.
又易知ABCD为等腰梯形,∠BAD=∠CDA=60°,
则作BM⊥AD于点M,CN⊥AD于点N,
∵AB=2,
∴AM=AB=1,
∴AM=DN=1,从而AD=4,
故△PCD的周长的最小值为6.
11.【答案】(1)r:a=1:1;;(2).
【解析】如图所示.
(1)连接圆心O和T1的6个顶点可得6个全等的正三角形,所以r:a=1:1;
连接圆心O和T2相邻的两个顶点,得以圆O半径为高的正三角形,所以.
(2)T∶T的边长比是∶2,所以S∶S= .
所以.
12.【答案】;
【解析】连结OA、OO′、.(如图所示)
∵⊙O与AB,AD相切,⊙O′与BC,CD相切,
∴OA平分∠BAD,O′C平分∠BCD, ∴∠BAO=∠BCO′=45°,
若连结AC,则∠BAC=45°,∴直线OO′与直线AC重合,
设⊙O切AB、AD于E、F,⊙O′切BC、CD于G、H.
∵⊙O与⊙O′互相外切,∴OO′=R+r.
连接OF、OE、、,则.
同理,
∴ .
又∵,∴ ,
∴ .
三、解答题
13.【答案与解析】
解:过P作AB的垂线,交AB、DE分别为H、K,连接BD,
∵六边形ABCDEF是正六边形,
∴AB∥DE,AF∥CD,BC∥EF,且P到AF与CD的距离和及P到EF、BC的距离和均为HK的长,
∵BC=CD,∠BCD=∠ABC=∠CDE=120°,
∴∠CBD=∠BDC=30°,
∴BD∥HK,且BD=HK,
∵CG⊥BD,
∴BD=2BG=6,
∴点P到各边距离之和为3BD=3×6=18.
14.【答案与解析】
(1)∠APB=120°(如图①)
∵点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动,
∴∠BAM=∠CBN,
又∵∠APN=∠BPM,
∴∠APN=∠BPM=∠ABN+∠BAM=∠ABN+∠CBN=∠ABC=60°,
∴∠APB=120°;
(2)同理可得:图②中∠APB=90°;图③中∠APB=72°.
(3)由(1)可知,∠APB=所在多边形的外角度数,故在图n中,∠APB=.
15.【答案与解析】
(1)①∵正20边形的每个内角的度数m==162°,
∴|180-m|=18;
②当“接近度”等于0时,正n边形就成了圆.
(2)不合理.例如,对两个相似而不全等的正n边形来说,它们接近于圆的程度是相同的,但|R-r|却不相等.合理定义方法不唯一,如定义为、越小,正n边形越接近于圆;越大,正n边形与圆的形状差异越大;当=1时,正n边形就变成了圆.
P
D
R
C
Q
B
O
A
【学习目标】
1.了解正多边形和圆的有关概念及对称性;
2.理解并掌握正多边形半径和边长、边心距、中心角之间的关系,会应用正多边形和圆的有关知识画正多边形;
3.会进行正多边形的有关计算.
【要点梳理】
要点一、正多边形的概念
各边相等,各角也相等的多边形是正多边形.
要点二、正多边形的重要元素
正多边形的外接圆和圆的内接正多边形
2.正多边形的有关概念
3.正多边形的有关计算
(1)正n边形每一个内角的度数是(N-2)180°/N;
(2)正n边形每个中心角的度数是360°/N;
(3)正n边形每个外角的度数是360°/N.
要点三、正多边形的性质
1.正多边形都只有一个外接圆,圆有无数个内接正多边形.
2.正n边形的半径和边心距把正n边形分成2n个全等的直角三角形.
3.正多边形都是轴对称图形,对称轴的条数与它的边数相同,每条对称轴都通过正n边形的中心;当边数是偶数时,它也是中心对称图形,它的中心就是对称中心.
4.边数相同的正多边形相似。它们周长的比,边心距的比,半径的比都等于相似比,面积的比等于相似比的平方.
5.任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆
要点四、正多边形的画法
1.用量角器等分圆
2.用尺规等分圆
【典型例题】
类型一、正多边形的概念
例1. 如图所示,正五边形的对角线AC和BE相交于点M.
(1)求证:AC∥ED;(2)求证:ME=AE.
例2.如图,正方形ABCD内接于⊙O,E为DC的中点,直线BE交⊙O于点F,若⊙O的半径为,则BF的长为 .
例3.如图,AG是正八边形ABCDEFGH的一条对角线.
(1)在剩余的顶点B、C、D、E、F、H中,连接两个顶点,使连接的线段与AG平行,并说明理由;
(2)两边延长AB、CD、EF、GH,使延长线分别交于点P、Q、M、N,若AB=2,求四边形PQMN的面积.
例4. 如图(1)所示,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G,求证:阴影部分四边形OFCG的面积是△ABC的面积的.
【巩固练习】
一、选择题
1. 已知等边三角形的内切圆半径,外接圆半径和高的比是( )
A.1:2:√3 B. 2:3:4 C. 1:√3:2 D. 1:2:3
2.将边长为3cm的正三角形各边三等分,以这六个分点为顶点构成一个正六边形,则这个正六边形的面积为 ( )
A. B.cm2 C.cm2 D.cm2
3.如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形, BC∥QR,则∠AOQ=( )
A.60° B.65° C.72° D.75°
第3题 第5题
4.周长是12的正三角形、正方形、正六边形的面积分别是S3、S4、S6,则它们的大小关系是( ).
A.S6>S4>S3 B.S3>S4>S6 C.S6>S3>S4 D.S4>S6>S3
5. 如图所示,八边形ABCDEFGH是正八边形,其外接⊙O的半径为,则正八边形的面积S为( ).
A. B. C. 8 D.4
6.先作半径为的圆的内接正方形,接着作上述内接正方形的内切圆,再作上述内切圆的内接正方形,…,则按以上规律作出的第7个圆的内接正方形的边长为( )
A. B. C. D.
二、填空题
7.一个正方形与圆有相等的周长,则圆面积与正方形的面积比为________.
8.如图所示,正六边形内接于圆O,圆O的半径为10,则图中阴影部分的面积为________.
半径相等的圆内接正三角形、正方形、正六边形的边长之比为
10.如图,在边长为2的正六边形ABCDEF中,点P是其对角线BE上一动点,连接PC、PD,则△PCD的周长的最小值是 .
11.如图所示,有一个圆O和两个正六边形T1、T2.T1的6个顶点都在圆周上,T2的6条边都和圆O相切(我们称T1,T2分别为圆O的内接正六边形和外切正六边形).
(1)设T1,T2的边长分别为a,b, 圆O的半径为r,则r:a= ; r:b= ;
(2)正六边形T1,T2的面积比S1:S2的值是 .
第11题图 第12题图
12.如图所示,已知正方形ABCD中,边长AB=3,⊙O与⊙O′外切且与正方形两边相切,两圆半径为R、r,则R+r= .
三、解答题
13.如图,正六边形ABCDEF的边长为2cm,点P为六边形内任一点.则点P到各边距离之和为多少cm?
14.如图①、②、③,正三角形ABC、正方形ABCD、正五边形ABCDE分别是⊙O的内接三角形、内接四边形、内接五边形,点M、N分别从点B、C开始,以相同的速度中⊙O上逆时针运动.
(1)求图①中∠APB的度数;
(2)图②中,∠APB的度数是 ,图③中∠APB的度数是 ;
(3)根据前面探索,你能否将本题推广到一般的正n边形情况?若能,写出推广问题和结论;若不能,请说明理由.
15.如图,正三角形、正方形、正六边形等正n边形与圆的形状有差异,我们将正n边形与圆的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设正n边形的每个内角的度数为m°,将正n边形的“接近度”定义为|180-m|.于是,|180-m|越小,该正n边形就越接近于圆,
①若n=20,则该正n边形的“接近度”等于 ;
②当“接近度”等于 时,正n边形就成了圆.
(2)设一个正n边形的半径(即正n边形外接圆的半径)为R,边心距(即正n边形的中心到各边的距离)为r,将正n边形的“接近度”定义为|R-r|,于是|R-r|越小,正n边形就越接近于圆.你认为这种说法是否合理?若不合理,请给出正n边形“接近度”的一个合理定义.
【答案与解析】
一、选择题
1.【答案】D;
【解析】解:图中内切圆半径是OD,外接圆的半径是OC,高是AD,
因而AD=OC+OD;
在直角△OCD中,∠DOC=60°,
则OD:OC=1:2,
因而OD:OC:AD=1:2:3,
所以内切圆半径,外接圆半径和高的比是1:2:3.故选D.
2.【答案】A;
【解析】所得正六边形边长为1,∴ .
3.【答案】D;
【解析】易求∠POQ=120°,∠AOP=45°,则∠AOQ=∠POQ-∠AOP=120°-45°=75°.
4.【答案】A;
【解析】如图(1),∵ AB=4,AD=2,∠OAD=30°,∴ OD=.
∴ .
如图(2),∵ AB=AC=3,∴ S4=3×3=9.
如图(3),∵ CD=2,∴ OC=2,CM=1,
∴ OM=.
∴ .
又∵ ,
∴ ,故选A.
5.【答案】B;
【解析】连接OA、OB,过A作AM⊥OB于M,
∵ ,
∴ △AOM是等腰直角三角形.
又,∴ AM=1,
∴ ,
∴ ,
6.【答案】A.
【解析】由于圆内接正方形的边长与圆的半径的比为,内接正方形的内切圆的半径与正方形的边长的比为0.5,
即这样做一次后,圆的内接正方形的边长为×=1;
做第二次后的正方形的边长为;
依次类推可得:第n个正方形的边长是()n-1,
则做第7次后的圆的内接正方形的边长为.
故选A.
二、填空题
7.【答案】 ;
【解析】 设正方形边长为a,则周长为4a,面积为,圆周长也为4a,则,
∴ ,∴
∴ .
8.【答案】;
【解析】图中阴影部分面积等于圆的面积减去正六边形的面积.
∵ ,
,
∴
9.【答案】::1;
【解析】设圆的半径为R,
如图(一),连接OB,过O作OD⊥BC于D,
则∠OBC=30°,BD=OB?cos30°=R,(或由勾股定理求)
故BC=2BD=R;
如图(二),连接OB、OC,过O作OE⊥BC于E,
则△OBE是等腰直角三角形,
2BE2=OB2,即BE=,
故BC=R;
如图(三),连接OA、OB,过O作OG⊥AB,
则△OAB是等边三角形,
故AG=OA?cos60°=R,AB=2AG=R,(或由勾股定理求)
故圆内接正三角形、正方形、正六边形的边长之比为R:R:R=::1.
10.【答案】6.
【解析】要使△PCD的周长的最小,即PC+PD最小.
利用正多边形的性质可得点C关于BE的对称点为点A,连接AD交BE于点P',那么有P'C=P'A,P'C+P'D=AD最小.
又易知ABCD为等腰梯形,∠BAD=∠CDA=60°,
则作BM⊥AD于点M,CN⊥AD于点N,
∵AB=2,
∴AM=AB=1,
∴AM=DN=1,从而AD=4,
故△PCD的周长的最小值为6.
11.【答案】(1)r:a=1:1;;(2).
【解析】如图所示.
(1)连接圆心O和T1的6个顶点可得6个全等的正三角形,所以r:a=1:1;
连接圆心O和T2相邻的两个顶点,得以圆O半径为高的正三角形,所以.
(2)T∶T的边长比是∶2,所以S∶S= .
所以.
12.【答案】;
【解析】连结OA、OO′、.(如图所示)
∵⊙O与AB,AD相切,⊙O′与BC,CD相切,
∴OA平分∠BAD,O′C平分∠BCD, ∴∠BAO=∠BCO′=45°,
若连结AC,则∠BAC=45°,∴直线OO′与直线AC重合,
设⊙O切AB、AD于E、F,⊙O′切BC、CD于G、H.
∵⊙O与⊙O′互相外切,∴OO′=R+r.
连接OF、OE、、,则.
同理,
∴ .
又∵,∴ ,
∴ .
三、解答题
13.【答案与解析】
解:过P作AB的垂线,交AB、DE分别为H、K,连接BD,
∵六边形ABCDEF是正六边形,
∴AB∥DE,AF∥CD,BC∥EF,且P到AF与CD的距离和及P到EF、BC的距离和均为HK的长,
∵BC=CD,∠BCD=∠ABC=∠CDE=120°,
∴∠CBD=∠BDC=30°,
∴BD∥HK,且BD=HK,
∵CG⊥BD,
∴BD=2BG=6,
∴点P到各边距离之和为3BD=3×6=18.
14.【答案与解析】
(1)∠APB=120°(如图①)
∵点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动,
∴∠BAM=∠CBN,
又∵∠APN=∠BPM,
∴∠APN=∠BPM=∠ABN+∠BAM=∠ABN+∠CBN=∠ABC=60°,
∴∠APB=120°;
(2)同理可得:图②中∠APB=90°;图③中∠APB=72°.
(3)由(1)可知,∠APB=所在多边形的外角度数,故在图n中,∠APB=.
15.【答案与解析】
(1)①∵正20边形的每个内角的度数m==162°,
∴|180-m|=18;
②当“接近度”等于0时,正n边形就成了圆.
(2)不合理.例如,对两个相似而不全等的正n边形来说,它们接近于圆的程度是相同的,但|R-r|却不相等.合理定义方法不唯一,如定义为、越小,正n边形越接近于圆;越大,正n边形与圆的形状差异越大;当=1时,正n边形就变成了圆.
P
D
R
C
Q
B
O
A
同课章节目录
