14.1.4 整式的乘法课时作业(2)
图片预览


文档简介
14.1 整式的乘法(7)
姓名:__________班级:__________考号:__________
一、选择题
1.a6÷a等于( )
A. a B. aa C. a5 D. a3
2.(﹣2018)0的值是( )
A.﹣2018 B.2018 C.0 D.1
3.计算(6x3﹣2x)÷(﹣2x)的结果是( )
A.﹣3x2 B.﹣3x2﹣1 C.﹣3x2+1 D.3x2﹣1
4.若xm÷x2n+1=x,则m与n的关系是( )
A.m=2n+1 B.m=﹣2n﹣1 C.m﹣2n=2 D.m﹣2n=﹣2
5.计算[(a+b)2﹣(a﹣b)2]÷(4ab)的结果( )
A.2ab B.1 C.a﹣b D.a+b
6.初中毕业时,张老师买了一些纪念品准备分发给学生.若这些纪念品可以平均分给班级的(n+3)名学生,也可以平均分给班级的(n﹣2)名学生(n为大于3的正整数),则用代数式表示这些纪念品的数量不可能是( )
A.n2+n﹣6 B. 2n2+2n﹣12 C. n2﹣n﹣6 D. n3+n2﹣6n
二、填空题
7.计算x7÷x4的结果等于 .
8.计算:|﹣1|+20= .
9.已知多项式x3﹣1x2+ax﹣1除以bx﹣1,商是x2﹣x+2,余式为1,a+b的值为 .
10.长方形面积是3a2﹣3ab+6a,一边长为3a,则它的另一边长是 .
11.①一个多项式除以2m得1﹣m+m2,这个多项式为 .
② ÷(2x+3)=(3x﹣2).
③小玉和小丽做游戏,两人各报一个整式,小玉报一个被除式,小丽报一个除式,要求商必须是3ab.若小玉报的是3a2b﹣ab2,则小丽报的是 ;若小丽报的是9a2b,则小玉报的整式是 .
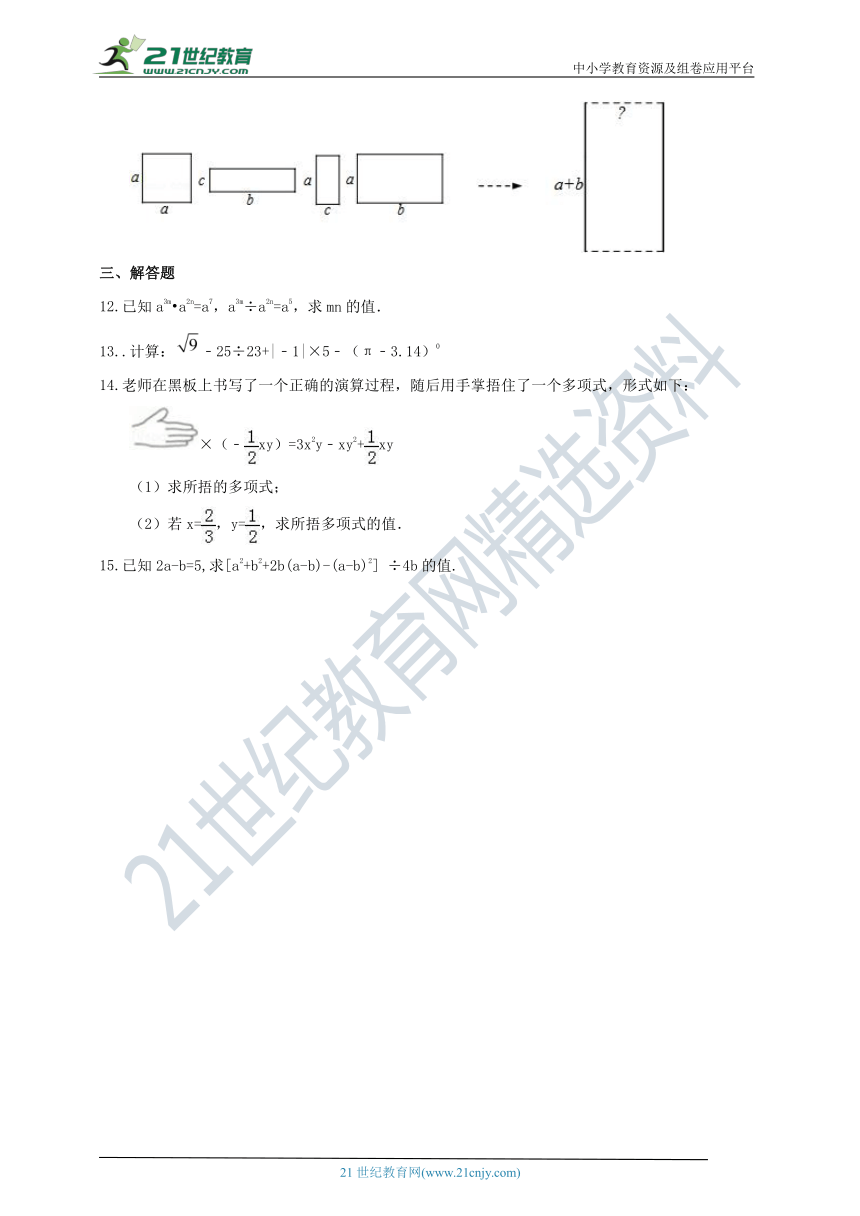
④如图甲、乙两个农民共有4块地,今年他们决定共同投资搞饲养业,为此他们准备将这4块地换成宽为(a+b)cm的地,为了使所换到的面积与原来地的总面积相等,交换之后的地的长应为 m.
三、解答题
12.已知a3m?a2n=a7,a3m÷a2n=a5,求mn的值.
13..计算:﹣25÷23+|﹣1|×5﹣(π﹣3.14)0
14.老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:
×(﹣xy)=3x2y﹣xy2+xy
(1)求所捂的多项式;
(2)若x=,y=,求所捂多项式的值.
15.已知2a-b=5,求[a2+b2+2b(a-b)-(a-b)2] ÷4b的值.
答案解析
一 、选择题
1.【考点】整式的除法.
【分析】根据整式的除法法则即可求出答案.
解:a6÷a=a5 ,故C项正确.
故选C.
【点评】此题主要考查了同底数幂的乘除运算,正确掌握运算法则是解题关键.
2.【考点】零指数幂
【分析】根据零指数幂的意义即可求解.
解:(﹣2018)0=1.
故选:D.
【点评】本题考查了零指数幂的意义,掌握a0=1(a≠0)是解题的关键.
3.【考点】整式的除法.
【分析】根据整式的除法法则即可求出答案.
解:原式=﹣3x2+1
故选(C)
【点评】此题主要考查了同底数幂的乘除运算,正确掌握运算法则是解题关键.
4.【考点】同底数幂的除法
【分析】直接利用同底数幂的乘除运算法则计算得出答案.
解:∵xm÷x2n+1=x,
∴m﹣2n﹣1=1,
则m﹣2n=2.
故选:C.
【点评】此题主要考查了同底数幂的乘除运算,正确掌握运算法则是解题关键.
5.【考点】整式的除法;完全平方公式.
【分析】直接利用完全平方公式化简进而利用整式除法运算法则求出答案.
解:[(a+b)2﹣(a﹣b)2]÷(4ab)
=(a2+b2+2ab﹣a2﹣b2+2ab)÷4ab
=4ab÷4ab
=1.
故选:B.
6.【考点】整式的除法.
【分析】根据题意及数的整除性对每个选项分析解答得出正确选项.
解:A、(n2+n﹣6)÷[(n+3)(n﹣2)]=1,即n2+n﹣6能被n+3和n﹣2整除,即能平均分,故本选项错误;
B、(2n2+2n﹣12)÷[(n+3)(n﹣2)]=2,即2n2+2n﹣12能被n+3和n﹣2整除,即能平均分,故本选项错误;
C、n2﹣n﹣6不能被(n+3)和(n﹣2)整除,即不能平均分,故本选项正确;
D、(n3+n2﹣6n)÷[(n+3)(n﹣2)]=n,即n3+n2﹣6n能被n+3和n﹣2整除,即能平均分,故本选项错误.
故选:C.
【点评】此题考查的知识点列代数式,解答此题的关键是用数的整除性分析论证得出正确选项.
二 、填空题
7.【考点】同底数幂的除法.
【分析】根据同底数幂的除法即可求出答案.
解:原式=x3,
故答案为:x3
8.【考点】零指数幂,绝对值
【分析】本题涉及零指数幂、绝对值2个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
解:|﹣1|+20
=1+1
=2.
故答案为:2.
【点评】本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握零指数幂、绝对值等考点的运算.
9.【考点】 整式的除法.
【分析】先根据被除式=除式×商式+余式,列出x3﹣x+ax﹣1=(bx﹣1)×(x2﹣x+2)+1,再将等式右边展开,合并同类项,利用两个多项式相等的条件即可求解.
解:由题意可知,x3﹣x+ax﹣1=(bx﹣1)×(x2﹣x+2)+1,
整理得:x3﹣x2+ax﹣1=bx3+(﹣b﹣1)x2+(2b+1)x﹣1,
∴b=0,a=2b+1,
∴a=1,b=0.
∴a+b=1.
故答案为1.
10.【考点】 整式的除法.
【分析】由长方形的面积求法可知由一边乘以另一边而得,则本题由面积除以边长可求得另一边.
解:∵长方形面积是3a2﹣3ab+6a,一边长为3a,
∴它的另一边长是:(3a2﹣3ab+6a)÷3a=a﹣b+2,
故答案为:a﹣b+2.
11.【考点】单项式乘多项式,多项式乘多项式,多项式除以多项式
【分析】单项式乘多项式,多项式乘多项式,多项式除以多项式的法则和长方形的面积公式求解
解:①2m(1﹣m+m2)=2m﹣2m2+2m3;
②(2x+3)(3x﹣2)=6x2+5x﹣6;
③(3a2b﹣ab2)÷3ab=a﹣b,
3ab?9a2b=27a3b2;
④∵原来4块地的总面积=a2+bc+ac+ab,
∴将这4块土地换成一块地后面积为(a2+bc+ac+ab)米,
而此块地的宽为(a+b)米,
∴此块地的长=(a2+bc+ac+ab)÷(a+b)
=(a2+ac+bc+ab)÷(a+b)
=[a(a+c)+b(a+c)]÷(a+b)
=(a+b)(a+c)÷(a+b)
=a+c.
故答案为:2m﹣2m2+2m3;6x2+5x﹣6;a﹣b,27a3b2;a+c.
【点睛】本题考查了单项式乘多项式,多项式乘多项式,多项式除以多项式的法则和长方形的面积公式,熟练掌握运算法则是关键
三 、解答题
12.【考点】同底数幂的乘法;同底数幂的除法
【分析】利用同底数幂的乘除法运算法则得出关于m,n等式,求出答案即可.
解:∵a3m?a2n=a7,a3m÷a2n=a5,
∴,
解得:,
故mn=2×=1.
【点评】此题主要考查了同底数幂的乘除法运算,正确掌握运算法则是解题关键.
13.【考点】平方根,有理数的乘方,绝对值,有理数的乘法,零指数幂
【分析】依据算术平方根的定义、有理数的乘方法则、绝对值的性质、有理数的 乘法法则、零指数幂的性质进行计算,最后,再进行加减计算即可.
解:原式=3﹣32÷8+5﹣1=3﹣4+5﹣1=3.
【点评】本题主要考查的是实数的运算,熟练掌握运算法则是解题的关键.
14.【考点】单项式乘多项式,多项式除以单项式的法
【分析】(1)设多项式为A,则A=(3x2y﹣xy2+xy)÷(﹣xy)计算即可.
(2)把x=,y=代入多项式求值即可.
解:(1)设多项式为A,
则A=(3x2y﹣xy2+xy)÷(﹣xy)=﹣6x+2y﹣1.
(2)∵x=,y=,
∴原式=﹣6×+2×﹣1=﹣4+1﹣1=﹣4.
【点评】本题考查单项式乘多项式、多项式除以单项式的法则,解题的关键是利用乘法与除法是互为逆运算,把乘法转化为除法解决问题,属于基础题.
15.【考点】整式的混合运算-化简求值
【分析】原式中括号中第二项利用单项式乘以多项式法则计算,第三项利用完全平方公式展开,去括号合并得到最简结果,再利用多项式除以单项式法则计算得到最简结果,然后将已知等式代入计算即可求出值.
解:原式=[a2+b2+2ab-2b2-(a2-2ab+b2)]÷4b
=[a2+b2+2ab-2b2-a2+2ab-b2]÷4b=[4ab-2b2]÷4b
=a-b= (2a-b).
当2a-b=5时,原式= (2a-b)= ×5=.
【点评】此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.
姓名:__________班级:__________考号:__________
一、选择题
1.a6÷a等于( )
A. a B. aa C. a5 D. a3
2.(﹣2018)0的值是( )
A.﹣2018 B.2018 C.0 D.1
3.计算(6x3﹣2x)÷(﹣2x)的结果是( )
A.﹣3x2 B.﹣3x2﹣1 C.﹣3x2+1 D.3x2﹣1
4.若xm÷x2n+1=x,则m与n的关系是( )
A.m=2n+1 B.m=﹣2n﹣1 C.m﹣2n=2 D.m﹣2n=﹣2
5.计算[(a+b)2﹣(a﹣b)2]÷(4ab)的结果( )
A.2ab B.1 C.a﹣b D.a+b
6.初中毕业时,张老师买了一些纪念品准备分发给学生.若这些纪念品可以平均分给班级的(n+3)名学生,也可以平均分给班级的(n﹣2)名学生(n为大于3的正整数),则用代数式表示这些纪念品的数量不可能是( )
A.n2+n﹣6 B. 2n2+2n﹣12 C. n2﹣n﹣6 D. n3+n2﹣6n
二、填空题
7.计算x7÷x4的结果等于 .
8.计算:|﹣1|+20= .
9.已知多项式x3﹣1x2+ax﹣1除以bx﹣1,商是x2﹣x+2,余式为1,a+b的值为 .
10.长方形面积是3a2﹣3ab+6a,一边长为3a,则它的另一边长是 .
11.①一个多项式除以2m得1﹣m+m2,这个多项式为 .
② ÷(2x+3)=(3x﹣2).
③小玉和小丽做游戏,两人各报一个整式,小玉报一个被除式,小丽报一个除式,要求商必须是3ab.若小玉报的是3a2b﹣ab2,则小丽报的是 ;若小丽报的是9a2b,则小玉报的整式是 .
④如图甲、乙两个农民共有4块地,今年他们决定共同投资搞饲养业,为此他们准备将这4块地换成宽为(a+b)cm的地,为了使所换到的面积与原来地的总面积相等,交换之后的地的长应为 m.
三、解答题
12.已知a3m?a2n=a7,a3m÷a2n=a5,求mn的值.
13..计算:﹣25÷23+|﹣1|×5﹣(π﹣3.14)0
14.老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:
×(﹣xy)=3x2y﹣xy2+xy
(1)求所捂的多项式;
(2)若x=,y=,求所捂多项式的值.
15.已知2a-b=5,求[a2+b2+2b(a-b)-(a-b)2] ÷4b的值.
答案解析
一 、选择题
1.【考点】整式的除法.
【分析】根据整式的除法法则即可求出答案.
解:a6÷a=a5 ,故C项正确.
故选C.
【点评】此题主要考查了同底数幂的乘除运算,正确掌握运算法则是解题关键.
2.【考点】零指数幂
【分析】根据零指数幂的意义即可求解.
解:(﹣2018)0=1.
故选:D.
【点评】本题考查了零指数幂的意义,掌握a0=1(a≠0)是解题的关键.
3.【考点】整式的除法.
【分析】根据整式的除法法则即可求出答案.
解:原式=﹣3x2+1
故选(C)
【点评】此题主要考查了同底数幂的乘除运算,正确掌握运算法则是解题关键.
4.【考点】同底数幂的除法
【分析】直接利用同底数幂的乘除运算法则计算得出答案.
解:∵xm÷x2n+1=x,
∴m﹣2n﹣1=1,
则m﹣2n=2.
故选:C.
【点评】此题主要考查了同底数幂的乘除运算,正确掌握运算法则是解题关键.
5.【考点】整式的除法;完全平方公式.
【分析】直接利用完全平方公式化简进而利用整式除法运算法则求出答案.
解:[(a+b)2﹣(a﹣b)2]÷(4ab)
=(a2+b2+2ab﹣a2﹣b2+2ab)÷4ab
=4ab÷4ab
=1.
故选:B.
6.【考点】整式的除法.
【分析】根据题意及数的整除性对每个选项分析解答得出正确选项.
解:A、(n2+n﹣6)÷[(n+3)(n﹣2)]=1,即n2+n﹣6能被n+3和n﹣2整除,即能平均分,故本选项错误;
B、(2n2+2n﹣12)÷[(n+3)(n﹣2)]=2,即2n2+2n﹣12能被n+3和n﹣2整除,即能平均分,故本选项错误;
C、n2﹣n﹣6不能被(n+3)和(n﹣2)整除,即不能平均分,故本选项正确;
D、(n3+n2﹣6n)÷[(n+3)(n﹣2)]=n,即n3+n2﹣6n能被n+3和n﹣2整除,即能平均分,故本选项错误.
故选:C.
【点评】此题考查的知识点列代数式,解答此题的关键是用数的整除性分析论证得出正确选项.
二 、填空题
7.【考点】同底数幂的除法.
【分析】根据同底数幂的除法即可求出答案.
解:原式=x3,
故答案为:x3
8.【考点】零指数幂,绝对值
【分析】本题涉及零指数幂、绝对值2个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
解:|﹣1|+20
=1+1
=2.
故答案为:2.
【点评】本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握零指数幂、绝对值等考点的运算.
9.【考点】 整式的除法.
【分析】先根据被除式=除式×商式+余式,列出x3﹣x+ax﹣1=(bx﹣1)×(x2﹣x+2)+1,再将等式右边展开,合并同类项,利用两个多项式相等的条件即可求解.
解:由题意可知,x3﹣x+ax﹣1=(bx﹣1)×(x2﹣x+2)+1,
整理得:x3﹣x2+ax﹣1=bx3+(﹣b﹣1)x2+(2b+1)x﹣1,
∴b=0,a=2b+1,
∴a=1,b=0.
∴a+b=1.
故答案为1.
10.【考点】 整式的除法.
【分析】由长方形的面积求法可知由一边乘以另一边而得,则本题由面积除以边长可求得另一边.
解:∵长方形面积是3a2﹣3ab+6a,一边长为3a,
∴它的另一边长是:(3a2﹣3ab+6a)÷3a=a﹣b+2,
故答案为:a﹣b+2.
11.【考点】单项式乘多项式,多项式乘多项式,多项式除以多项式
【分析】单项式乘多项式,多项式乘多项式,多项式除以多项式的法则和长方形的面积公式求解
解:①2m(1﹣m+m2)=2m﹣2m2+2m3;
②(2x+3)(3x﹣2)=6x2+5x﹣6;
③(3a2b﹣ab2)÷3ab=a﹣b,
3ab?9a2b=27a3b2;
④∵原来4块地的总面积=a2+bc+ac+ab,
∴将这4块土地换成一块地后面积为(a2+bc+ac+ab)米,
而此块地的宽为(a+b)米,
∴此块地的长=(a2+bc+ac+ab)÷(a+b)
=(a2+ac+bc+ab)÷(a+b)
=[a(a+c)+b(a+c)]÷(a+b)
=(a+b)(a+c)÷(a+b)
=a+c.
故答案为:2m﹣2m2+2m3;6x2+5x﹣6;a﹣b,27a3b2;a+c.
【点睛】本题考查了单项式乘多项式,多项式乘多项式,多项式除以多项式的法则和长方形的面积公式,熟练掌握运算法则是关键
三 、解答题
12.【考点】同底数幂的乘法;同底数幂的除法
【分析】利用同底数幂的乘除法运算法则得出关于m,n等式,求出答案即可.
解:∵a3m?a2n=a7,a3m÷a2n=a5,
∴,
解得:,
故mn=2×=1.
【点评】此题主要考查了同底数幂的乘除法运算,正确掌握运算法则是解题关键.
13.【考点】平方根,有理数的乘方,绝对值,有理数的乘法,零指数幂
【分析】依据算术平方根的定义、有理数的乘方法则、绝对值的性质、有理数的 乘法法则、零指数幂的性质进行计算,最后,再进行加减计算即可.
解:原式=3﹣32÷8+5﹣1=3﹣4+5﹣1=3.
【点评】本题主要考查的是实数的运算,熟练掌握运算法则是解题的关键.
14.【考点】单项式乘多项式,多项式除以单项式的法
【分析】(1)设多项式为A,则A=(3x2y﹣xy2+xy)÷(﹣xy)计算即可.
(2)把x=,y=代入多项式求值即可.
解:(1)设多项式为A,
则A=(3x2y﹣xy2+xy)÷(﹣xy)=﹣6x+2y﹣1.
(2)∵x=,y=,
∴原式=﹣6×+2×﹣1=﹣4+1﹣1=﹣4.
【点评】本题考查单项式乘多项式、多项式除以单项式的法则,解题的关键是利用乘法与除法是互为逆运算,把乘法转化为除法解决问题,属于基础题.
15.【考点】整式的混合运算-化简求值
【分析】原式中括号中第二项利用单项式乘以多项式法则计算,第三项利用完全平方公式展开,去括号合并得到最简结果,再利用多项式除以单项式法则计算得到最简结果,然后将已知等式代入计算即可求出值.
解:原式=[a2+b2+2ab-2b2-(a2-2ab+b2)]÷4b
=[a2+b2+2ab-2b2-a2+2ab-b2]÷4b=[4ab-2b2]÷4b
=a-b= (2a-b).
当2a-b=5时,原式= (2a-b)= ×5=.
【点评】此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.
