2018年高中数学第1章立体几何初步1.2.2空间两条直线的位置关系课件9苏教版必修2(23张)
文档属性
| 名称 | 2018年高中数学第1章立体几何初步1.2.2空间两条直线的位置关系课件9苏教版必修2(23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 00:00:00 | ||
图片预览








文档简介
课件23张PPT。复习:平面内两条直线的位置关系相交直线
(有一个公共点)平行直线
(无公共点)两路相交立交桥立交桥中, 两条路线AB, CD既不平行,又不相交观察实例 黑板两侧所在的直线与课桌边沿所在直线是什么位置关系?既不平行
又不相交 旗杆所在的直线与长安街所在直线是什么位置关系?既不平行
又不相交 在下面长方体中,直线AB与AD,AB与CD,AB和CC’的位置关系又是怎样的呢? 不同在任何一个平面内的两条直线叫做异面直线。没有只有一个没有共面不共面共面1.异面直线的定义
两直线异面的判别一 :
两条直线 既不相交、又不平行.
两直线异面的判别二 :
两条直线不同在任何一个平面内.
1 2 3
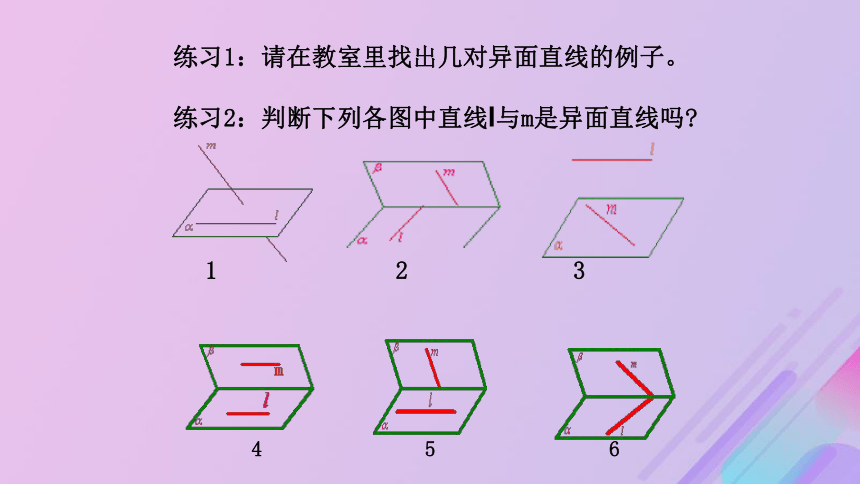
练习1:请在教室里找出几对异面直线的例子。
练习2:判断下列各图中直线l与m是异面直线吗?
4 5 6
合作探究一:
如下图我们能否说直线l与直线m是异面直线?
如何才能体现两条异面直线异面呢?2.异面直线的画法说明: 画异面直线时 , 为了体现
它们不共面的特点。常借
助一个或两个平面来衬托.如图:(1)(3)(2)a与b是相交直线a与b是平行直线a与b是异面直线答:不一定:它们可能异面,可能相交,也可能平行。 分别在两个平面内的两条直线是否一定异面?合作探究二空间两条直线的位置关系有且只有三种3、空间中两条直线的位置关系巩固练习
在如图所示的正方体中,指出哪些棱所在的直线与直线BA1是异面直线?ABCDA1B1D1C14.?空间两平行直线提出问题:
在同一平面内,如果两条直线都与第三条直线平行,那么这两条直线互相平行。在空间中,是否有类似的规律?公理4:平行于同一条直线的两条直线互相平行.注:
1.直线a,b,c 两两平行,可记为a // b // c .2.公理4所表述的性质,叫做空间平行线的传递性.平行公理例题示范 如图:在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点。
求证:四边形EFGH是平行四边形。分析:欲证EFGH是一个平行四边形只需证EH∥FG且EH=FGE,F,G,H分别是各边中点连结BD,只需证:
EH ∥BD且EH = BD
FG ∥BD且FG = BD例1 如图 ,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形。所以EH//BD,且 证明:连接BD,因为 EH是 的中位线,同理FG//BD,且 所以 EH//FG,且EH=FG 所以,四边形EFGH是平行四边形。例1变式: 在例2中,如果再加上条件AC=BD,那么四边形EFGH是什么图形? EHFG分析:
在例题2的基础上我们只需要证明平行四边形的两条邻边相等。菱形课堂小结不同在任何一个平面内的两条直线叫做异面直线。一、异面直线的定义:相交直线 平行直线异面直线二、空间两直线的位置关系四、平行公理平行于同一条直线的两条直线互相平行.三、异面直线的画法
(用一个或两个平面衬托) 课本P45 探究
(要求:动手剪出这个展开图并折成正方体演示,找出异面直线是哪些,然后把展开图贴在作业本上。)作业:2)a与b是异面直线,b与c是异面直线,则a与c是异面直线。3)a与b是共面,b与c是共面,则a与c共面。错错错1)a α,b α,则a,b一定异面。一、判断随堂练习1. 两条直线a,b分别和异面直线c,d都相交,则直线a,b的位置关系是( )
A. 一定是异面直线
B. 一定是相交直线
C. 可能是平行直线
D. 可能是异面直线,也可能是相交直线
2. 一条直线和两条异面直线中的一条平行,则它和另一条的位置关系是( )
A.平行 B.相交
C.异面 D.相交或异面二、选择DD3. 分别在两个平面内的两条直线间的位置关系是( )A.异面 B.平行
C.相交 D.以上都有可能
4. 异面直线a,b满足a??,b??,?∩?=l,则l与a,b的位置关系一定是( )
A. l与a,b都相交
B .l至少与a,b中的一条相交
C. l至多与a,b中的一条相交
D. l至少与a,b中的一条平行BD
(有一个公共点)平行直线
(无公共点)两路相交立交桥立交桥中, 两条路线AB, CD既不平行,又不相交观察实例 黑板两侧所在的直线与课桌边沿所在直线是什么位置关系?既不平行
又不相交 旗杆所在的直线与长安街所在直线是什么位置关系?既不平行
又不相交 在下面长方体中,直线AB与AD,AB与CD,AB和CC’的位置关系又是怎样的呢? 不同在任何一个平面内的两条直线叫做异面直线。没有只有一个没有共面不共面共面1.异面直线的定义
两直线异面的判别一 :
两条直线 既不相交、又不平行.
两直线异面的判别二 :
两条直线不同在任何一个平面内.
1 2 3
练习1:请在教室里找出几对异面直线的例子。
练习2:判断下列各图中直线l与m是异面直线吗?
4 5 6
合作探究一:
如下图我们能否说直线l与直线m是异面直线?
如何才能体现两条异面直线异面呢?2.异面直线的画法说明: 画异面直线时 , 为了体现
它们不共面的特点。常借
助一个或两个平面来衬托.如图:(1)(3)(2)a与b是相交直线a与b是平行直线a与b是异面直线答:不一定:它们可能异面,可能相交,也可能平行。 分别在两个平面内的两条直线是否一定异面?合作探究二空间两条直线的位置关系有且只有三种3、空间中两条直线的位置关系巩固练习
在如图所示的正方体中,指出哪些棱所在的直线与直线BA1是异面直线?ABCDA1B1D1C14.?空间两平行直线提出问题:
在同一平面内,如果两条直线都与第三条直线平行,那么这两条直线互相平行。在空间中,是否有类似的规律?公理4:平行于同一条直线的两条直线互相平行.注:
1.直线a,b,c 两两平行,可记为a // b // c .2.公理4所表述的性质,叫做空间平行线的传递性.平行公理例题示范 如图:在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点。
求证:四边形EFGH是平行四边形。分析:欲证EFGH是一个平行四边形只需证EH∥FG且EH=FGE,F,G,H分别是各边中点连结BD,只需证:
EH ∥BD且EH = BD
FG ∥BD且FG = BD例1 如图 ,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形。所以EH//BD,且 证明:连接BD,因为 EH是 的中位线,同理FG//BD,且 所以 EH//FG,且EH=FG 所以,四边形EFGH是平行四边形。例1变式: 在例2中,如果再加上条件AC=BD,那么四边形EFGH是什么图形? EHFG分析:
在例题2的基础上我们只需要证明平行四边形的两条邻边相等。菱形课堂小结不同在任何一个平面内的两条直线叫做异面直线。一、异面直线的定义:相交直线 平行直线异面直线二、空间两直线的位置关系四、平行公理平行于同一条直线的两条直线互相平行.三、异面直线的画法
(用一个或两个平面衬托) 课本P45 探究
(要求:动手剪出这个展开图并折成正方体演示,找出异面直线是哪些,然后把展开图贴在作业本上。)作业:2)a与b是异面直线,b与c是异面直线,则a与c是异面直线。3)a与b是共面,b与c是共面,则a与c共面。错错错1)a α,b α,则a,b一定异面。一、判断随堂练习1. 两条直线a,b分别和异面直线c,d都相交,则直线a,b的位置关系是( )
A. 一定是异面直线
B. 一定是相交直线
C. 可能是平行直线
D. 可能是异面直线,也可能是相交直线
2. 一条直线和两条异面直线中的一条平行,则它和另一条的位置关系是( )
A.平行 B.相交
C.异面 D.相交或异面二、选择DD3. 分别在两个平面内的两条直线间的位置关系是( )A.异面 B.平行
C.相交 D.以上都有可能
4. 异面直线a,b满足a??,b??,?∩?=l,则l与a,b的位置关系一定是( )
A. l与a,b都相交
B .l至少与a,b中的一条相交
C. l至多与a,b中的一条相交
D. l至少与a,b中的一条平行BD
