2018年高中数学第2章平面解析几何初步2.1.2直线的方程课件11苏教版必修2(15张)
文档属性
| 名称 | 2018年高中数学第2章平面解析几何初步2.1.2直线的方程课件11苏教版必修2(15张) |  | |
| 格式 | zip | ||
| 文件大小 | 844.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 15:34:34 | ||
图片预览






文档简介
课件15张PPT。 笛卡尔(Rene
Descartes,公元
1596年3月31日——
公元1650年2月11日)
法国著名的数学家、哲
学家、物理学家,成功
地将当时完全分开的代
数和几何学联系到了一
起。由于他创立了著名的平面直角坐标系,因此,被人称为解析几何之父。后人将解
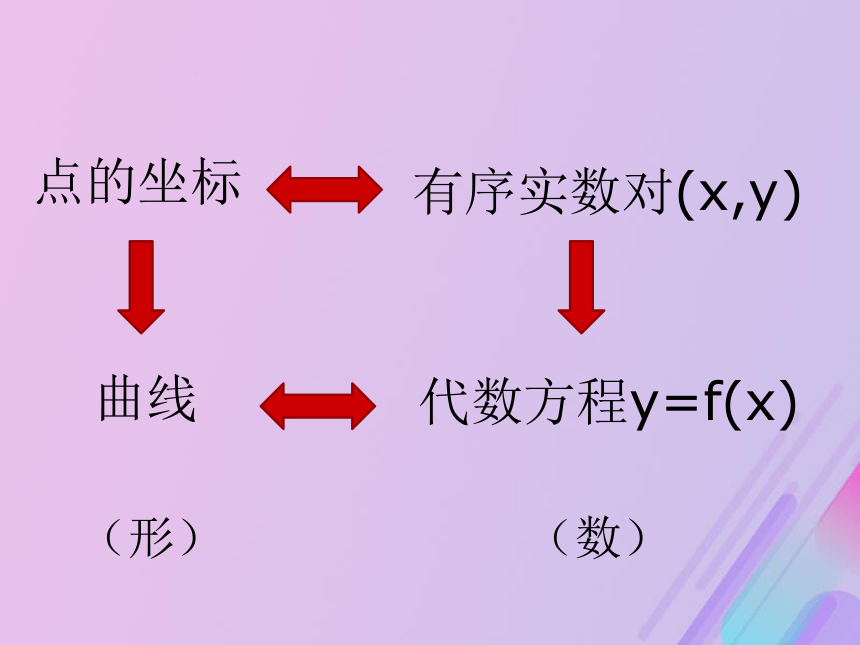
析几何与对数、微积分并称为17世纪三大数学成就。点的坐标有序实数对(x,y)曲线代数方程y=f(x)(形)(数)直线圆椭圆双曲线抛物线必修2选修1-1 若直线l经过点A(-1,3),斜率为-2,点P(x,y)在直线l上运动,那么
点P的坐标x和y之间满足什么关系?点P与定点A(-1,3)所确定的直线的斜率恒等于-2,故有:即: 即 . 由此,我们得到经过点A(-1,3),斜率为-2的直线方程是 .问题二问: 1.直线l上的点的坐标是否都满足方程? 2.以此方程的解为坐标的点是否在直线l上? 直线l经过点P1(x1,y1),斜率为k,点P在直线l上运动,那么点
P的坐标(x,y)满足什么条件?当点P(x,y)在直线l上运动时,PP1的斜率恒等于k,即 ,故 .由此,这个方程 就是过点P1 ,斜率为k的直线l的方程。探究活动例1:已知一直线经过点P(-2,3),斜率为2,求这条直线的方程。解:由直线的点斜式方程,得即 .2.若一直线经过点P(1,2),且倾斜角与直线y=2x+3的
倾斜角相等,求该直线方程变式.若一直线经过点P(1,2),且倾斜角是直线y=2x+3的倾斜角的两倍,求该直线方程例2:已知直线l 斜率为k,与y轴的交点是P(0,b),求直线l的方程。解:由直线的点斜式方程,得即为 .其中,b为直线与y轴交点的纵坐标。 我们称b为直线l 在y轴上的截距。 方程 由直线l的斜率和它在y轴上的截距确定 。 所以,这个方程 就也叫做直线的斜截式方程。2- 4- 240XXX课堂思考:点斜式和斜截式之间能否相互转化?
Descartes,公元
1596年3月31日——
公元1650年2月11日)
法国著名的数学家、哲
学家、物理学家,成功
地将当时完全分开的代
数和几何学联系到了一
起。由于他创立了著名的平面直角坐标系,因此,被人称为解析几何之父。后人将解
析几何与对数、微积分并称为17世纪三大数学成就。点的坐标有序实数对(x,y)曲线代数方程y=f(x)(形)(数)直线圆椭圆双曲线抛物线必修2选修1-1 若直线l经过点A(-1,3),斜率为-2,点P(x,y)在直线l上运动,那么
点P的坐标x和y之间满足什么关系?点P与定点A(-1,3)所确定的直线的斜率恒等于-2,故有:即: 即 . 由此,我们得到经过点A(-1,3),斜率为-2的直线方程是 .问题二问: 1.直线l上的点的坐标是否都满足方程? 2.以此方程的解为坐标的点是否在直线l上? 直线l经过点P1(x1,y1),斜率为k,点P在直线l上运动,那么点
P的坐标(x,y)满足什么条件?当点P(x,y)在直线l上运动时,PP1的斜率恒等于k,即 ,故 .由此,这个方程 就是过点P1 ,斜率为k的直线l的方程。探究活动例1:已知一直线经过点P(-2,3),斜率为2,求这条直线的方程。解:由直线的点斜式方程,得即 .2.若一直线经过点P(1,2),且倾斜角与直线y=2x+3的
倾斜角相等,求该直线方程变式.若一直线经过点P(1,2),且倾斜角是直线y=2x+3的倾斜角的两倍,求该直线方程例2:已知直线l 斜率为k,与y轴的交点是P(0,b),求直线l的方程。解:由直线的点斜式方程,得即为 .其中,b为直线与y轴交点的纵坐标。 我们称b为直线l 在y轴上的截距。 方程 由直线l的斜率和它在y轴上的截距确定 。 所以,这个方程 就也叫做直线的斜截式方程。2- 4- 240XXX课堂思考:点斜式和斜截式之间能否相互转化?
