2018年高中数学第3章空间向量与立体几何3.1.2共面向量定理课件3苏教版选修2_1(18张)
文档属性
| 名称 | 2018年高中数学第3章空间向量与立体几何3.1.2共面向量定理课件3苏教版选修2_1(18张) |  | |
| 格式 | zip | ||
| 文件大小 | 185.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 16:53:52 | ||
图片预览






文档简介
课件18张PPT。
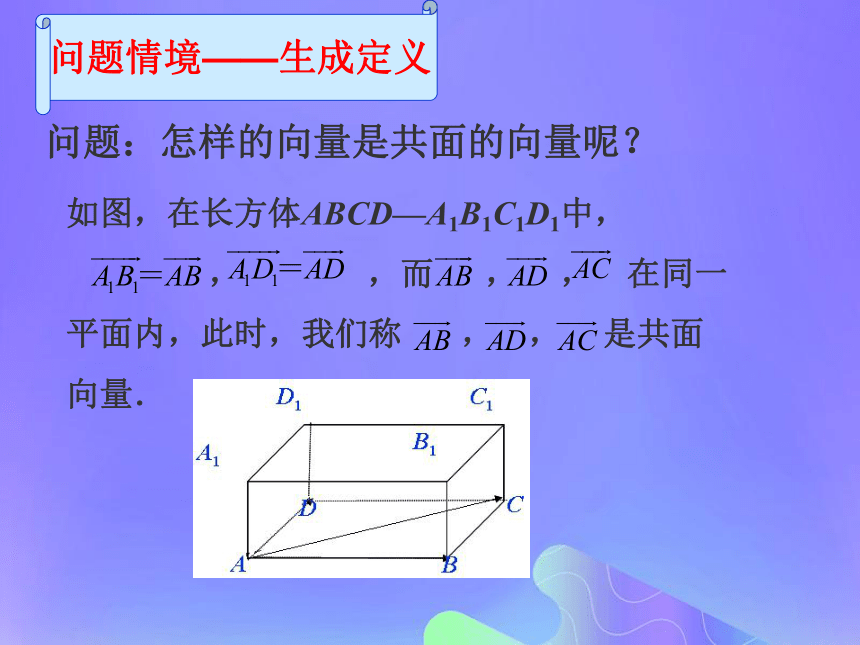
向量共面定理概念回顾——温故知新1 .向量的共线定理.2 .平面向量基本定理.问题情境——生成定义问题:怎样的向量是共面的向量呢? 问题情境——生成定义共面向量的定义:
一般地,能平移到同一个平面内的向量叫共面向量; (2)空间任意两个向量是共面的,但空间任意三个向量就不一定共面了.注意:(1)若 , 为不共线且同在平面α内,则 与 , 共面的意义是 在α内或 ∥ α .学生活动—探究问题在平面向量中,向量 与向量 ( ≠0)共线的充要条件是存在实数λ,使得 =λ .
那么,空间任意一个向量 与两个不共线的向量 , 共面时,它们之间存在什么样的关系呢?学生活动—探究问题探究1:空间任意向量 与两不共线向量 ,共面时,他们之间存在怎样的关系呢?存在有序实数组(x,y),使得
=x +y .学生活动—探究问题
探究2:空间任意向量 与两不共线向量 ,
存在有序实数组(x,y),使得
=x +y .那么向量 与 , 共面吗?共面向量定理: 如果两个向量 , 不共线,那么向量 与向量 , 共面的充要条件是存在有序实数组(x,y),使得
=x +y . 这就是说,向量 可以由不共线的两个向量 , 线性表示.思考:
共面向量定理与平面向量基本定理 的联系?两者不仅在形式上是相同的,而且在本质上也是一致的.数学应用证明:又 与 不共线
根据共面向量定理,可知 , , 共面.
由于MN不在平面CDE中,
所以MN//平面CDE.特点:向量法由计算结果得出几何结论,大大减弱了推理论证的成分,可以避免有一定难度的构作辅线等过程. 注意:最后要对运算结果的几何意义做出解释,从而解决立体几何的问题. 对于平面任意一点满足向量关系
(其中x+y=1)
则 P,A,B三点共线.数学应用—探究拓展探究3:你能否类比推广到空间给出相似的结论吗?例2 设空间任意一点O和不共线的三点A,B,C,若点P满足向量关系
(其中x+y+z=1)
试问 P,A,B,C四点是否共面?数学应用—探究拓展练习:1.已知A,B,M三点不共线,对于平面ABM外的任一点O,确定在下列各条件下,点P是否与A,B,M一定共面?注意:
空间四点P,M,A,B共面实数对练一练练一 练(2)已知平行四边形ABCD,从平面AC外一点O引向量, 求证:①四点E,F,G,H共面;
②平面AC∥平面EG.回顾反思——小结收获本节课学习了以下内容:
1.了解共面向量的含义;
2.理解共面向量定理;
3.能运用共面向量定理证明有关线面平行和点共面的简单问题. 反馈训练——课后作业 课本P97习题3.1:8,9.
谢谢
向量共面定理概念回顾——温故知新1 .向量的共线定理.2 .平面向量基本定理.问题情境——生成定义问题:怎样的向量是共面的向量呢? 问题情境——生成定义共面向量的定义:
一般地,能平移到同一个平面内的向量叫共面向量; (2)空间任意两个向量是共面的,但空间任意三个向量就不一定共面了.注意:(1)若 , 为不共线且同在平面α内,则 与 , 共面的意义是 在α内或 ∥ α .学生活动—探究问题在平面向量中,向量 与向量 ( ≠0)共线的充要条件是存在实数λ,使得 =λ .
那么,空间任意一个向量 与两个不共线的向量 , 共面时,它们之间存在什么样的关系呢?学生活动—探究问题探究1:空间任意向量 与两不共线向量 ,共面时,他们之间存在怎样的关系呢?存在有序实数组(x,y),使得
=x +y .学生活动—探究问题
探究2:空间任意向量 与两不共线向量 ,
存在有序实数组(x,y),使得
=x +y .那么向量 与 , 共面吗?共面向量定理: 如果两个向量 , 不共线,那么向量 与向量 , 共面的充要条件是存在有序实数组(x,y),使得
=x +y . 这就是说,向量 可以由不共线的两个向量 , 线性表示.思考:
共面向量定理与平面向量基本定理 的联系?两者不仅在形式上是相同的,而且在本质上也是一致的.数学应用证明:又 与 不共线
根据共面向量定理,可知 , , 共面.
由于MN不在平面CDE中,
所以MN//平面CDE.特点:向量法由计算结果得出几何结论,大大减弱了推理论证的成分,可以避免有一定难度的构作辅线等过程. 注意:最后要对运算结果的几何意义做出解释,从而解决立体几何的问题. 对于平面任意一点满足向量关系
(其中x+y=1)
则 P,A,B三点共线.数学应用—探究拓展探究3:你能否类比推广到空间给出相似的结论吗?例2 设空间任意一点O和不共线的三点A,B,C,若点P满足向量关系
(其中x+y+z=1)
试问 P,A,B,C四点是否共面?数学应用—探究拓展练习:1.已知A,B,M三点不共线,对于平面ABM外的任一点O,确定在下列各条件下,点P是否与A,B,M一定共面?注意:
空间四点P,M,A,B共面实数对练一练练一 练(2)已知平行四边形ABCD,从平面AC外一点O引向量, 求证:①四点E,F,G,H共面;
②平面AC∥平面EG.回顾反思——小结收获本节课学习了以下内容:
1.了解共面向量的含义;
2.理解共面向量定理;
3.能运用共面向量定理证明有关线面平行和点共面的简单问题. 反馈训练——课后作业 课本P97习题3.1:8,9.
谢谢
