2018年高中数学第3章空间向量与立体几何3.2.3空间的角的计算课件2苏教版选修2_1(13张)
文档属性
| 名称 | 2018年高中数学第3章空间向量与立体几何3.2.3空间的角的计算课件2苏教版选修2_1(13张) |

|
|
| 格式 | zip | ||
| 文件大小 | 353.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 16:55:12 | ||
图片预览




文档简介
课件13张PPT。3.2空间向量的应用
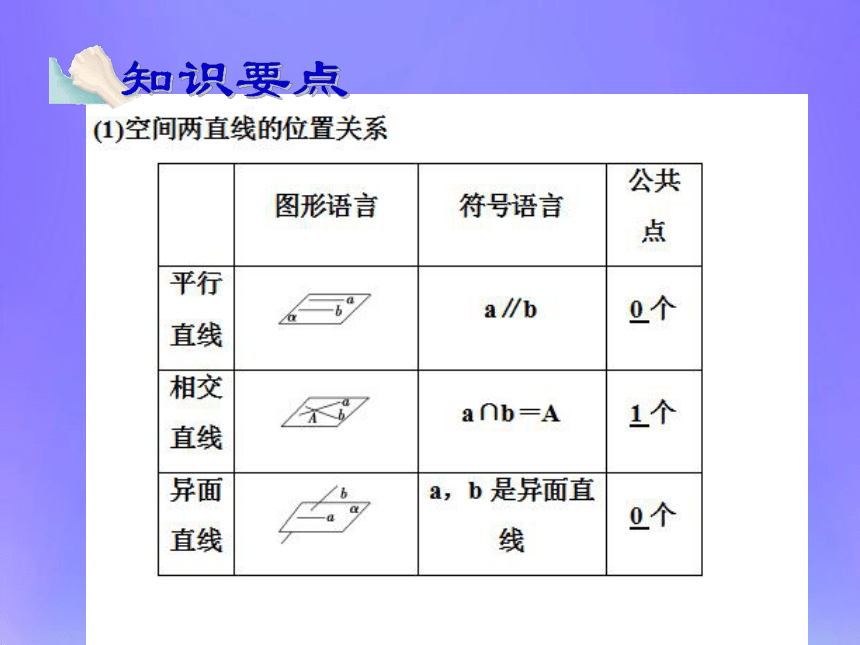
——空间角的计算(1)结论:合作探究1.空间直线所成角的范围: 思考:
直线的方向向量的夹角和
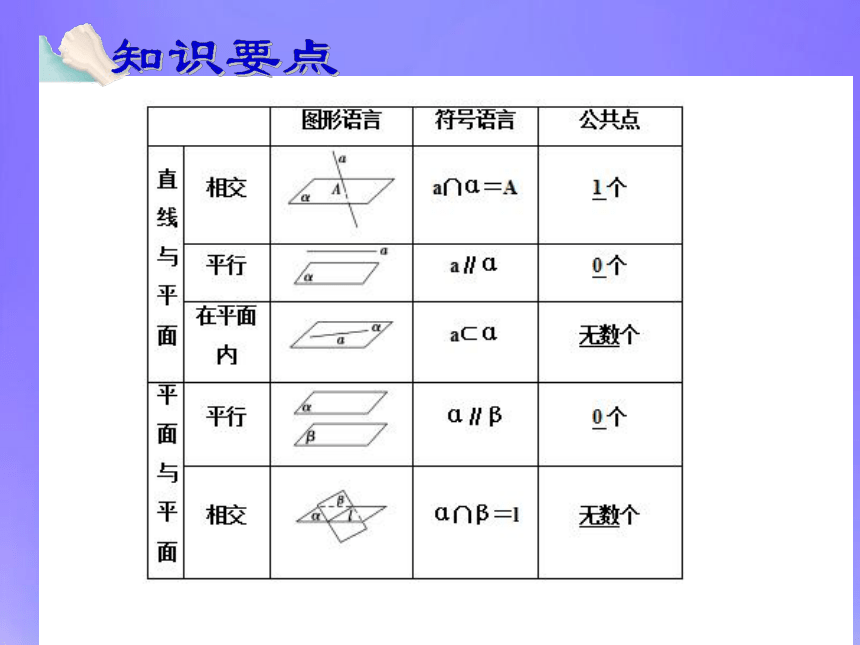
直线间的夹角有什么关系?合作探究2.直线与平面所成角的范围: 结论:思考:
方向向量与法向量所成角
和线面角有什么关系?例1.在正方体ABCD-A1B1C1D1中,棱长为2,点E1,F1,G
分别为A1B1,C1D1,BC的中点,
求(1)直线BE1与AC1所成的角的余弦值;
(2)直线D1G与平面ACD1所成角的正弦值。所以BE1与DF1所成角的余弦为解:以D为原点, , , 为正交基底建系.故例1.在正方体ABCD-A1B1C1D1中,棱长为2,点E1,F1,G
分别为A1B1,C1D1,BC的中点,
求(1)直线BE1与AC1所成的角的余弦值;
(2)直线D1G与平面ACD1所成角的正弦值。由题可知由题可知(2)设平面ACD1的法向量为则 故 所以所以直线D1G与平面ACD1所成角的
正弦值为课堂小结1.本节课你学习了哪些知识?2.你掌握了哪些方法? 空间中线线关系、线面关系、面面关系;线线角、线面角的范围;空间中线线角与直线方向向量夹角之间的关系;线面角与直线方向向量、平面法向量夹角之间的关系。几何法;利用直线的方向向量求线线角的方法、利用直线的方向向量和平面的法向量求线面角的方法;利用直线的方向向量求线线角时既可以用坐标运算,又可以转化为已知向量。3.体现了哪些数学思想?化归转化的思想;数形结合的思想;类比的思想1.两直线所成角: 2.直线与平面所成角: 课堂小结3.利用直线方向向量和平面法向量求线线、
线面所成角 谢谢大家!
直线的方向向量的夹角和
直线间的夹角有什么关系?合作探究2.直线与平面所成角的范围: 结论:思考:
方向向量与法向量所成角
和线面角有什么关系?例1.在正方体ABCD-A1B1C1D1中,棱长为2,点E1,F1,G
分别为A1B1,C1D1,BC的中点,
求(1)直线BE1与AC1所成的角的余弦值;
(2)直线D1G与平面ACD1所成角的正弦值。所以BE1与DF1所成角的余弦为解:以D为原点, , , 为正交基底建系.故例1.在正方体ABCD-A1B1C1D1中,棱长为2,点E1,F1,G
分别为A1B1,C1D1,BC的中点,
求(1)直线BE1与AC1所成的角的余弦值;
(2)直线D1G与平面ACD1所成角的正弦值。由题可知由题可知(2)设平面ACD1的法向量为则 故 所以所以直线D1G与平面ACD1所成角的
正弦值为课堂小结1.本节课你学习了哪些知识?2.你掌握了哪些方法? 空间中线线关系、线面关系、面面关系;线线角、线面角的范围;空间中线线角与直线方向向量夹角之间的关系;线面角与直线方向向量、平面法向量夹角之间的关系。几何法;利用直线的方向向量求线线角的方法、利用直线的方向向量和平面的法向量求线面角的方法;利用直线的方向向量求线线角时既可以用坐标运算,又可以转化为已知向量。3.体现了哪些数学思想?化归转化的思想;数形结合的思想;类比的思想1.两直线所成角: 2.直线与平面所成角: 课堂小结3.利用直线方向向量和平面法向量求线线、
线面所成角 谢谢大家!
