2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.2.1双曲线及其标准方程课件(19张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.2.1双曲线及其标准方程课件(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 00:00:00 | ||
图片预览






文档简介
课件19张PPT。2.2.1双曲线及其标准方程生活中的双曲线玉枕的形状可口可乐的下半部巴西利亚大教堂北京摩天大楼法拉利主题公园花瓶1. 椭圆定义: 2. 引入问题:复习引入数学实验:[1]取一条拉链;
[2]如图把它固定在
板上的两点F1、F2;
[3] 拉动拉链头(M)。
探寻双曲线的形成过程
思考:1、余下一段
拉链的目的是什么?
2、谁是动点,谁是定点
3、动点的轨迹是什么?
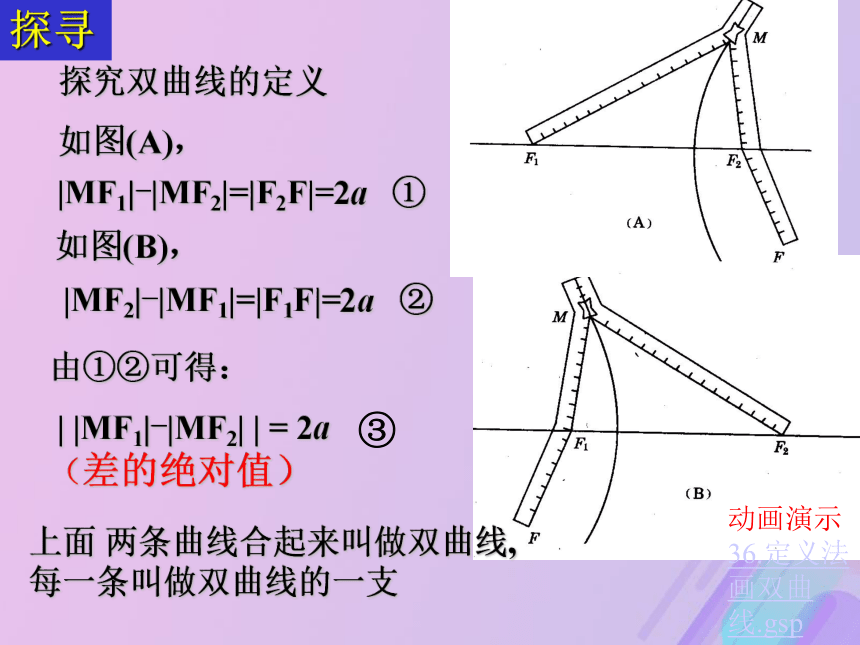
探究双曲线的定义
如图(A), |MF1|-|MF2|=|F2F|=2a ①如图(B),上面 两条曲线合起来叫做双曲线,
每一条叫做双曲线的一支由①②可得: | |MF1|-|MF2| | = 2a
(差的绝对值) |MF2|-|MF1|=|F1F|=2a ②探寻动画演示36.定义法画双曲线.gsp③一.双曲线的定义:课本P45
平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于︱F1F2︱)的点的轨迹叫做双曲线.新知① 两个定点F1、F2——双曲线的焦点;② |F1F2|=2c ——焦距.思考: (下面内容记录到书上或笔记本上)(2)若2a= |F1F2|,则轨迹是?(3)若2a> |F1F2|,则轨迹是?(4)若2a=0, 则轨迹是? 以F1、F2为端点的两条射线 轨迹不存在 线段F1F2的垂直平分线(1)将定义当中的绝对值如果去掉,那么点的轨迹是?1.动点P到点M(-1,0)的距离与到点N(1,0)的距离之差为2,则点P的轨迹是( )
A.双曲线 B.双曲线的一支
C.两条射线 D.一条射线D当堂训练 求曲线方程的步骤:双曲线的标准方程1.建系.2.设点.设M(x , y),则F1(-c,0),F2(c,0)3.列式|MF1| - |MF2|=±2a4.化简探寻二此即为焦点在x轴上的双曲线的标准方程c2=a2+b2 | |MF1|-|MF2| | = 2a
双曲线的标准方程(a>0, b>0)a不一定大于b新知(a>0, b>0)看x2、y2的系数,哪个为正,
焦点就在哪个 坐标轴上x轴上y轴上F1(-c,0), F2(c,0) 或a>0,b>0,但a不一定大于b,c2=a2+b2a>b>0,a2=b2+c2||MF1|-|MF2||=2a |MF1|+|MF2|=2a F1(0,-c), F2(0,c)F1(0,-c), F2(0,c)双曲线与椭圆之间的区别与联系F1(-c,0), F2(c,0) 或(±5,0)知识迁移 深化认知(一)基础练习
1.判断下列双曲线的焦点在哪个轴上,并且写出焦点坐标.知识迁移 深化认知(二)典型例题例1.已知双曲线的焦点为F1(-5,0), F2(5,0),双曲线上一点到焦点的距离差的绝对值等于6,则
(1) a=_______ , c =_______ , b =_______
(2) 双曲线的标准方程为______________354例2:求适合下列条件的双曲线的标准方程
(1)焦点为F1(0,-6),F2(0,6),过点M(2,-5)
(2)双曲线经过点 (1)解:解法一(待定系数法)将点(2,-5)代入方程,得又因为两式联立得:故所求双曲线的标准方程为:设所求双曲线的方程为
(1)焦点为F1(0,-6),F2(0,6),过点M(2,-5)
(1)解法二(定义法)根据双曲线的定义,有:又c=6,所以已知双曲线的焦点在y轴上,所以所求双曲线的标准方程为
(1)焦点为F1(0,-6),F2(0,6),过点M(2,-5)
(2) 解:设双曲线的方程为 因为双曲线经过已知两点,故得:所以所求双曲线的标准方程为(2)双曲线经过点 例3:如果方程 表示双曲线,求m的取值范围.解:知识迁移 深化认知| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)双曲线定义及标准方程小结a不一定大于b(a>0, b>0)
[2]如图把它固定在
板上的两点F1、F2;
[3] 拉动拉链头(M)。
探寻双曲线的形成过程
思考:1、余下一段
拉链的目的是什么?
2、谁是动点,谁是定点
3、动点的轨迹是什么?
探究双曲线的定义
如图(A), |MF1|-|MF2|=|F2F|=2a ①如图(B),上面 两条曲线合起来叫做双曲线,
每一条叫做双曲线的一支由①②可得: | |MF1|-|MF2| | = 2a
(差的绝对值) |MF2|-|MF1|=|F1F|=2a ②探寻动画演示36.定义法画双曲线.gsp③一.双曲线的定义:课本P45
平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于︱F1F2︱)的点的轨迹叫做双曲线.新知① 两个定点F1、F2——双曲线的焦点;② |F1F2|=2c ——焦距.思考: (下面内容记录到书上或笔记本上)(2)若2a= |F1F2|,则轨迹是?(3)若2a> |F1F2|,则轨迹是?(4)若2a=0, 则轨迹是? 以F1、F2为端点的两条射线 轨迹不存在 线段F1F2的垂直平分线(1)将定义当中的绝对值如果去掉,那么点的轨迹是?1.动点P到点M(-1,0)的距离与到点N(1,0)的距离之差为2,则点P的轨迹是( )
A.双曲线 B.双曲线的一支
C.两条射线 D.一条射线D当堂训练 求曲线方程的步骤:双曲线的标准方程1.建系.2.设点.设M(x , y),则F1(-c,0),F2(c,0)3.列式|MF1| - |MF2|=±2a4.化简探寻二此即为焦点在x轴上的双曲线的标准方程c2=a2+b2 | |MF1|-|MF2| | = 2a
双曲线的标准方程(a>0, b>0)a不一定大于b新知(a>0, b>0)看x2、y2的系数,哪个为正,
焦点就在哪个 坐标轴上x轴上y轴上F1(-c,0), F2(c,0) 或a>0,b>0,但a不一定大于b,c2=a2+b2a>b>0,a2=b2+c2||MF1|-|MF2||=2a |MF1|+|MF2|=2a F1(0,-c), F2(0,c)F1(0,-c), F2(0,c)双曲线与椭圆之间的区别与联系F1(-c,0), F2(c,0) 或(±5,0)知识迁移 深化认知(一)基础练习
1.判断下列双曲线的焦点在哪个轴上,并且写出焦点坐标.知识迁移 深化认知(二)典型例题例1.已知双曲线的焦点为F1(-5,0), F2(5,0),双曲线上一点到焦点的距离差的绝对值等于6,则
(1) a=_______ , c =_______ , b =_______
(2) 双曲线的标准方程为______________354例2:求适合下列条件的双曲线的标准方程
(1)焦点为F1(0,-6),F2(0,6),过点M(2,-5)
(2)双曲线经过点 (1)解:解法一(待定系数法)将点(2,-5)代入方程,得又因为两式联立得:故所求双曲线的标准方程为:设所求双曲线的方程为
(1)焦点为F1(0,-6),F2(0,6),过点M(2,-5)
(1)解法二(定义法)根据双曲线的定义,有:又c=6,所以已知双曲线的焦点在y轴上,所以所求双曲线的标准方程为
(1)焦点为F1(0,-6),F2(0,6),过点M(2,-5)
(2) 解:设双曲线的方程为 因为双曲线经过已知两点,故得:所以所求双曲线的标准方程为(2)双曲线经过点 例3:如果方程 表示双曲线,求m的取值范围.解:知识迁移 深化认知| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)双曲线定义及标准方程小结a不一定大于b(a>0, b>0)
