2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.3.1抛物线级其标准方程课件(13张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.3.1抛物线级其标准方程课件(13张) |

|
|
| 格式 | zip | ||
| 文件大小 | 683.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 16:57:55 | ||
图片预览



文档简介
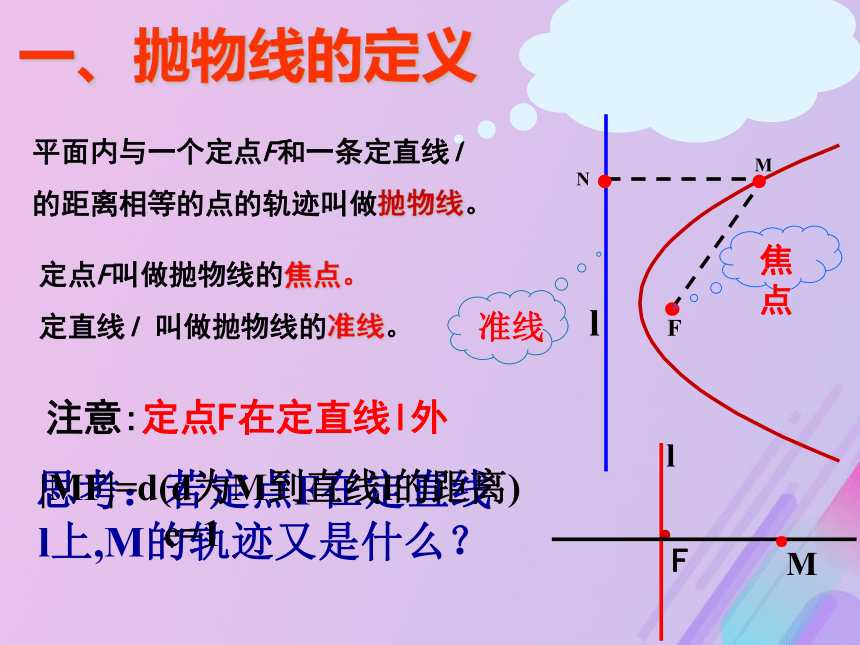
课件16张PPT。抛物线及其标准方程平面内与一个定点F和一条定直线l
的距离相等的点的轨迹叫做抛物线。一、抛物线的定义定点F叫做抛物线的焦点。
定直线l 叫做抛物线的准线。Fl·lFMN注意:定点F在定直线l外焦点|MF|=d(d为M到直线l的距离)
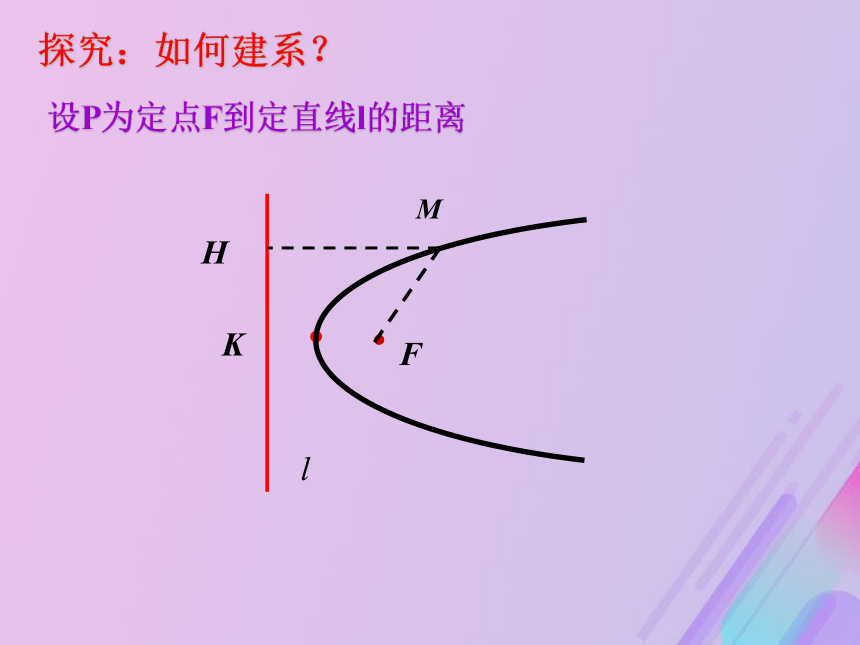
e=1二、抛物线的标准方程思考:求曲线方程的基本步骤是怎样的? 1、建系、设点 2、找出适合题意的曲线上任意点
的关系式; 3、将关系式坐标化为方程 4、化 简
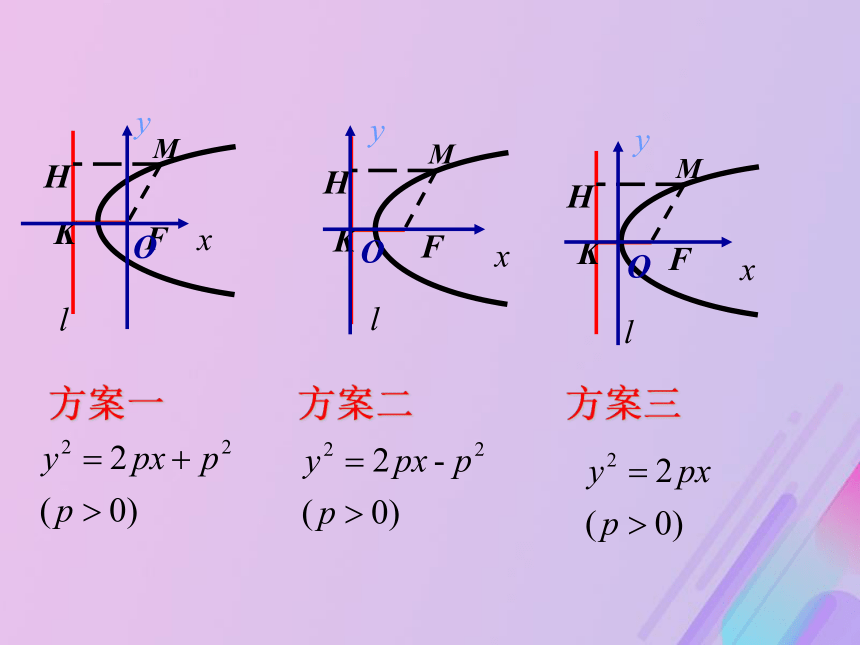
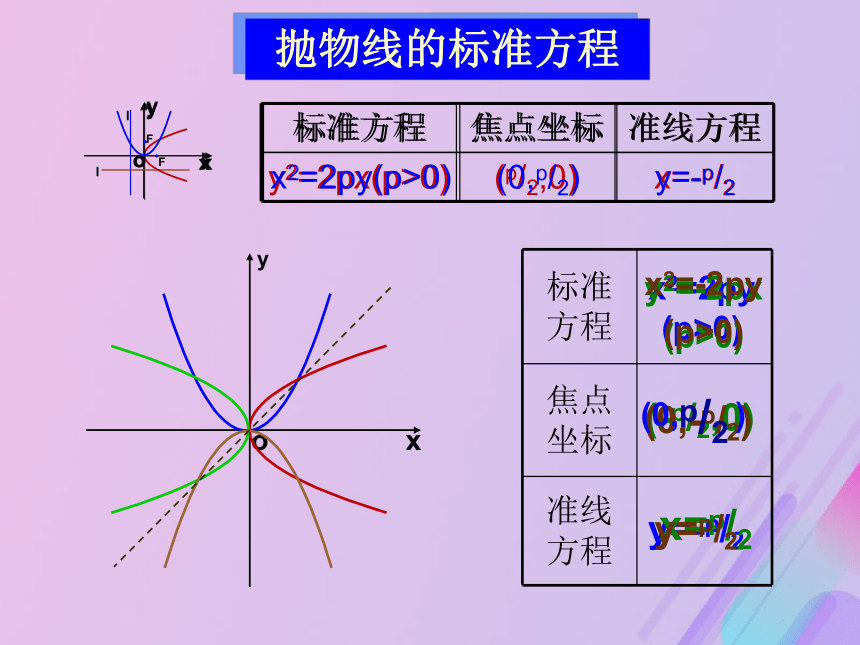
5、检验·探究:如何建系?设P为定点F到定直线l的距离方案一 方案二 方案三 把方程 y2 = 2px(p>0) 叫做抛物线的标准方程而p 的几何意义是: 焦点到准线的距离抛物线的标准方程(简称:“焦准距”)xyo抛物线的标准方程x2=2py(p>0)y=-p/2y2=-2px
(p>0)(-p/2,0)x=p/2
x2=-2py
(p>0)(0,-p/2)y=p/210:52:12四种抛物线的标准方程对比例1 求下列抛物线的焦点坐标和准线方程;
(1)y2= 4x,解:(1) ∵2P=4,∴P=2
所以抛物线的焦点坐标是( 1 ,0)
准线方程是x= -1
典例分析(2) y = 6 x 2 例1 (3) 已知抛物线的焦点坐标是F(0,-2),求它的 标准方程。
(4) 已知抛物线的准线方程为 ,求它的标准方程。 (2)标准方程为y2=-x
变式1:求抛物线 的焦点坐标和准线方程y =ax2(a≠0)变式2:
求过点A(-3,2)的抛物线的标准方程。
yxx2=2pyy2=-2px10:52:12例2、求抛物线 上与焦点的距离等于9的点的坐标3、求标准方程的方法:(1)待定系数法
(2)定义法小 结 :2、抛物线的标准方程类型与图象的对应
关系以及判断方法1、抛物线的定义、标准方程和它
的焦点、准线方程1、根据下列条件,写出抛物线的标准方程:当堂自测:(1)焦点是F(3,0);(2)准线方程 是(3)焦点到准线的距离是2.y2 =12xx2=yy2 =4x、 y2 = -4x、
x2 =4y 或 x2 = -4yD 3、已知抛物线的顶点在原点,对称轴为x轴,抛物线上的点
M(-3,m)到焦点的距离等于5,则抛物线的方程为____________,
m的值等于________.4、若点M到点F(4,0)的距离比它到直线l:x+5=0的距离少1,求点M的轨迹方程.
的距离相等的点的轨迹叫做抛物线。一、抛物线的定义定点F叫做抛物线的焦点。
定直线l 叫做抛物线的准线。Fl·lFMN注意:定点F在定直线l外焦点|MF|=d(d为M到直线l的距离)
e=1二、抛物线的标准方程思考:求曲线方程的基本步骤是怎样的? 1、建系、设点 2、找出适合题意的曲线上任意点
的关系式; 3、将关系式坐标化为方程 4、化 简
5、检验·探究:如何建系?设P为定点F到定直线l的距离方案一 方案二 方案三 把方程 y2 = 2px(p>0) 叫做抛物线的标准方程而p 的几何意义是: 焦点到准线的距离抛物线的标准方程(简称:“焦准距”)xyo抛物线的标准方程x2=2py(p>0)y=-p/2y2=-2px
(p>0)(-p/2,0)x=p/2
x2=-2py
(p>0)(0,-p/2)y=p/210:52:12四种抛物线的标准方程对比例1 求下列抛物线的焦点坐标和准线方程;
(1)y2= 4x,解:(1) ∵2P=4,∴P=2
所以抛物线的焦点坐标是( 1 ,0)
准线方程是x= -1
典例分析(2) y = 6 x 2 例1 (3) 已知抛物线的焦点坐标是F(0,-2),求它的 标准方程。
(4) 已知抛物线的准线方程为 ,求它的标准方程。 (2)标准方程为y2=-x
变式1:求抛物线 的焦点坐标和准线方程y =ax2(a≠0)变式2:
求过点A(-3,2)的抛物线的标准方程。
yxx2=2pyy2=-2px10:52:12例2、求抛物线 上与焦点的距离等于9的点的坐标3、求标准方程的方法:(1)待定系数法
(2)定义法小 结 :2、抛物线的标准方程类型与图象的对应
关系以及判断方法1、抛物线的定义、标准方程和它
的焦点、准线方程1、根据下列条件,写出抛物线的标准方程:当堂自测:(1)焦点是F(3,0);(2)准线方程 是(3)焦点到准线的距离是2.y2 =12xx2=yy2 =4x、 y2 = -4x、
x2 =4y 或 x2 = -4yD 3、已知抛物线的顶点在原点,对称轴为x轴,抛物线上的点
M(-3,m)到焦点的距离等于5,则抛物线的方程为____________,
m的值等于________.4、若点M到点F(4,0)的距离比它到直线l:x+5=0的距离少1,求点M的轨迹方程.
