2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.3.1利用导数判断函数的单调性课件(21张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.3.1利用导数判断函数的单调性课件(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 463.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 00:00:00 | ||
图片预览








文档简介
课件21张PPT。利用导数判断函数的单调性(4)对数函数的导数:(5)指数函数的导数: (3)三角函数 : 一、复习回顾:基本初等函数的导数公式导数运算法则函数 y = f (x) 在给定区间 G 上,当 x 1、x 2 ∈G 且 x 1< x 2 时函数单调性判定单调函数的图象特征1)都有 f ( x 1 ) < f ( x 2 ),则 f ( x ) 在G 上是增函数;2)都有 f ( x 1 ) > f ( x 2 ),则 f ( x ) 在G 上是减函数;若 f(x) 在G上是增函数或减函数,增函数减函数则 f(x) 在G上具有严格的单调性。G 称为单调区间G = ( a , b )二、复习引入:(1)函数的单调性也叫函数的增减性; (2)函数的单调性是对某个区间而言的,它是个局部概
念。这个区间是定义域的子集。(3)单调区间:针对自变量x而言的。
若函数在此区间上是增函数,则为单调递增区间;
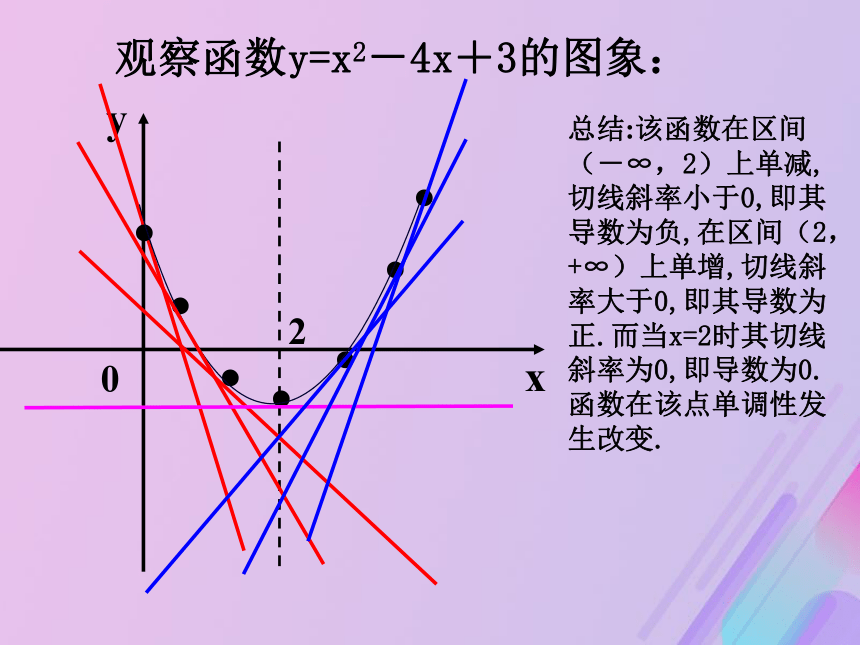
若函数在此区间上是减函数,则为单调递减区间。 以前,我们用定义来判断函数的单调性.在假设x1?[1,+∞)(-∞,1]cosx增自主检测题单调性与导数有什么关系?精讲精析.观察函数y=x2-4x+3的图象:总结:该函数在区间
(-∞,2)上单减,
切线斜率小于0,即其
导数为负,在区间(2,+∞)上单增,切线斜率大于0,即其导数为正.而当x=2时其切线斜率为0,即导数为0.
函数在该点单调性发生改变. 设函数y=f(x)在某个区间内有导数,如果在这个区间内y ′ >0,那么y=f(x)为这个区间内的增函数;如果在这个区间内y ′ <0,那么y=f(x)为这个区间内的减函数. 判断函数单调性的常用方法:
(1)定义法
(2)导数法 结论:y ′ >0增函数y ′ <0减函数 思考:也就是说“f′(x)>0”是“y=f(x)在某个区间上递增”的充分不必要条件.例1 确定函数f(x)=x2-2x+4在哪个区间内是增函数,哪个区间内是减函数.解:f′(x)=(x2-2x+4)′=2x-2.令2x-2>0,解得x>1.
∴当x∈(1,+∞)时,
f′(x)>0,f(x)是增函数.令2x-2<0,解得x<1.
∴当x∈(-∞,1)时,f′(x)<0,f(x)是减函数 例题讲解例2 确定函数f(x)=2x3-6x2+7在哪个区间
内是增函数,哪个区间内是减函数.解:f′(x)=(2x3-6x2+7)′=6x2-12x令6x2-12x>0,解得x>2或x<0∴当x∈(-∞,0)时,f′(x)>0,
f(x)是增函数.
当x∈(2,+∞)时,f′(x)>0,
f(x)是增函数.令6x2-12x<0,解得0<x<2.
∴当x∈(0,2)时,f′(x)<0,f(x)是减函数. 用导数法确定函数的单调性时的步骤是:
(1)求出函数的导函数
(2)求解不等式f ′(x)>0,求得其解集,
再根据解集写出单调递增区间
(3)求解不等式f ′(x)<0,求得其解集,
再根据解集写出单调递减区间注:单调区间不以“并集”出现。 2、导数的应用:判断单调性、求单调区间练习题1.函数y=3x-x3的单调增区间是( )
(A) (0,+∞) (B) (-∞,-1)
(C) (-1,1) (D) (1,+∞)2.设f(x)=x+ (x<0),则f(x)的单调增区间是( )
(A) (-∞,-2)
(B) (-2,0)
(C) (-∞,- )
(D) (- ,0)例3.如图,设有圆C和定点O,当l 从l0 开始在平面上绕O点匀速旋转(旋转角度不超过90°)时,它扫过的圆内阴影部分的面积S是时间t的函数,它的图象大致是下列四种情况中的哪一种?解:由于是匀速旋转,阴影部分的面积S(t)开始和最后时段缓慢增加,中间时段S增速快,
图A表示S的增速是常数,与实际不符,图A应否定;
图B表示最后时段S的增速快,也与实际不符,图B也应否定;
图C表示开始时段与最后时段S的增速快,也与实际不符,图C也应否定;
图D表示开始与结束时段,S的增速慢,中间的时段增速快,符合实际,应选D。练习:如图, 水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中, 请分别找出与各容器对应的水的高度h与时间t的函数关系图象.(A)(B)(C)(D)htOhtOhtOhtO 一般地, 如果一个函数在某一范围内导数的绝对值较大, 那么函数在这个范围内变化得快, 这时, 函数的图象就比较“陡峭”(向上或向下); 反之, 函数的图象就“平缓”一些. 如图,函数 在 或 内的图象“陡峭”,在 或 内的图象“平缓”.通过函数图像,不仅可以看出函数的增或减,还可以看出其变化的快慢,结合图像,从导数的角度解释变化快慢的情况。∴f(x1)-f(x2)>0,即f(x1)>f(x2)
∴f(x)= 在(0,+∞)上是减函数.
例4 证明函数f(x)= 在(0,+∞)上是减函数.证法一:(用以前学的方法证)任取两个数x1,x2∈(0,+∞)设x1<x2.f(x1)-f(x2)=∵x1>0,x2>0,∴x1x2>0
∵x1<x2,∴x2-x1>0, ∴ >0点评:比较一下两种方法,用求导证明是不是更简捷一些.如果是更复杂一些的函数,用导数的符号判别函数的增减性更能显示出它的优越性.
证法二:(用导数方法证)∵f′(x)=( )′=(-1)·x-2=- ,x>0,∴x2>0,∴- <0. ∴f′(x)<0,∴f(x)= 在(0,+∞)上是减函数.总结:求函数y=f(x)单调区间的步骤:
念。这个区间是定义域的子集。(3)单调区间:针对自变量x而言的。
若函数在此区间上是增函数,则为单调递增区间;
若函数在此区间上是减函数,则为单调递减区间。 以前,我们用定义来判断函数的单调性.在假设x1
(-∞,2)上单减,
切线斜率小于0,即其
导数为负,在区间(2,+∞)上单增,切线斜率大于0,即其导数为正.而当x=2时其切线斜率为0,即导数为0.
函数在该点单调性发生改变. 设函数y=f(x)在某个区间内有导数,如果在这个区间内y ′ >0,那么y=f(x)为这个区间内的增函数;如果在这个区间内y ′ <0,那么y=f(x)为这个区间内的减函数. 判断函数单调性的常用方法:
(1)定义法
(2)导数法 结论:y ′ >0增函数y ′ <0减函数 思考:也就是说“f′(x)>0”是“y=f(x)在某个区间上递增”的充分不必要条件.例1 确定函数f(x)=x2-2x+4在哪个区间内是增函数,哪个区间内是减函数.解:f′(x)=(x2-2x+4)′=2x-2.令2x-2>0,解得x>1.
∴当x∈(1,+∞)时,
f′(x)>0,f(x)是增函数.令2x-2<0,解得x<1.
∴当x∈(-∞,1)时,f′(x)<0,f(x)是减函数 例题讲解例2 确定函数f(x)=2x3-6x2+7在哪个区间
内是增函数,哪个区间内是减函数.解:f′(x)=(2x3-6x2+7)′=6x2-12x令6x2-12x>0,解得x>2或x<0∴当x∈(-∞,0)时,f′(x)>0,
f(x)是增函数.
当x∈(2,+∞)时,f′(x)>0,
f(x)是增函数.令6x2-12x<0,解得0<x<2.
∴当x∈(0,2)时,f′(x)<0,f(x)是减函数. 用导数法确定函数的单调性时的步骤是:
(1)求出函数的导函数
(2)求解不等式f ′(x)>0,求得其解集,
再根据解集写出单调递增区间
(3)求解不等式f ′(x)<0,求得其解集,
再根据解集写出单调递减区间注:单调区间不以“并集”出现。 2、导数的应用:判断单调性、求单调区间练习题1.函数y=3x-x3的单调增区间是( )
(A) (0,+∞) (B) (-∞,-1)
(C) (-1,1) (D) (1,+∞)2.设f(x)=x+ (x<0),则f(x)的单调增区间是( )
(A) (-∞,-2)
(B) (-2,0)
(C) (-∞,- )
(D) (- ,0)例3.如图,设有圆C和定点O,当l 从l0 开始在平面上绕O点匀速旋转(旋转角度不超过90°)时,它扫过的圆内阴影部分的面积S是时间t的函数,它的图象大致是下列四种情况中的哪一种?解:由于是匀速旋转,阴影部分的面积S(t)开始和最后时段缓慢增加,中间时段S增速快,
图A表示S的增速是常数,与实际不符,图A应否定;
图B表示最后时段S的增速快,也与实际不符,图B也应否定;
图C表示开始时段与最后时段S的增速快,也与实际不符,图C也应否定;
图D表示开始与结束时段,S的增速慢,中间的时段增速快,符合实际,应选D。练习:如图, 水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中, 请分别找出与各容器对应的水的高度h与时间t的函数关系图象.(A)(B)(C)(D)htOhtOhtOhtO 一般地, 如果一个函数在某一范围内导数的绝对值较大, 那么函数在这个范围内变化得快, 这时, 函数的图象就比较“陡峭”(向上或向下); 反之, 函数的图象就“平缓”一些. 如图,函数 在 或 内的图象“陡峭”,在 或 内的图象“平缓”.通过函数图像,不仅可以看出函数的增或减,还可以看出其变化的快慢,结合图像,从导数的角度解释变化快慢的情况。∴f(x1)-f(x2)>0,即f(x1)>f(x2)
∴f(x)= 在(0,+∞)上是减函数.
例4 证明函数f(x)= 在(0,+∞)上是减函数.证法一:(用以前学的方法证)任取两个数x1,x2∈(0,+∞)设x1<x2.f(x1)-f(x2)=∵x1>0,x2>0,∴x1x2>0
∵x1<x2,∴x2-x1>0, ∴ >0点评:比较一下两种方法,用求导证明是不是更简捷一些.如果是更复杂一些的函数,用导数的符号判别函数的增减性更能显示出它的优越性.
证法二:(用导数方法证)∵f′(x)=( )′=(-1)·x-2=- ,x>0,∴x2>0,∴- <0. ∴f′(x)<0,∴f(x)= 在(0,+∞)上是减函数.总结:求函数y=f(x)单调区间的步骤:
