2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.3.2利用导数研究函数的极值课件(13张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.3.2利用导数研究函数的极值课件(13张) |

|
|
| 格式 | zip | ||
| 文件大小 | 622.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 00:00:00 | ||
图片预览





文档简介
课件20张PPT。 3.3.2 利用导数研究函数的极值复习回顾在某个区间(a,b)内,
如果f ?(x)>0,那么函数y=f (x)在这个区间内________;
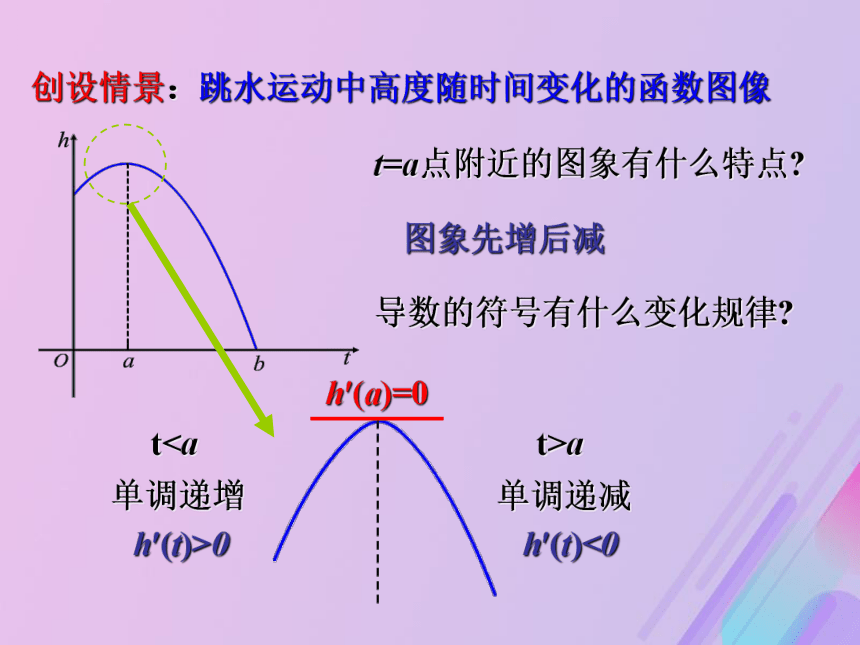
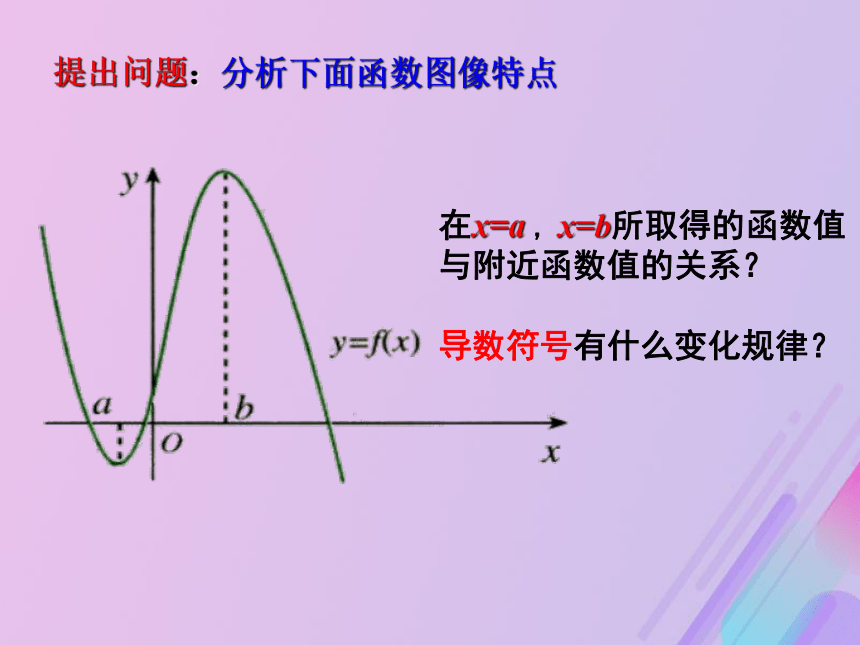
如果f ?(x)<0,那么函数y=f (x)在这个区间内________.单调递增单调递减几何画板t=a点附近的图象有什么特点?导数的符号有什么变化规律?创设情景:跳水运动中高度随时间变化的函数图像t>at0单调递增单调递减h?(a)=0图象先增后减提出问题:分析下面函数图像特点在x=a , x=b所取得的函数值与附近函数值的关系?
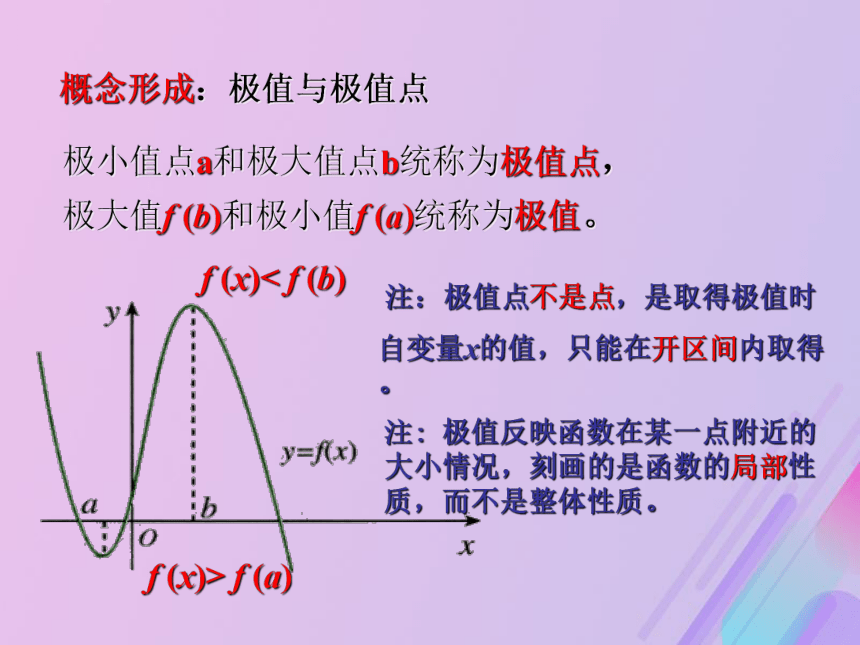
导数符号有什么变化规律?概念形成:极值与极值点极小值点a和极大值点b统称为极值点,
极大值f (b)和极小值f (a)统称为极值。 注:极值点不是点,是取得极值时
自变量x的值,只能在开区间内取得。注: 极值反映函数在某一点附近的大小情况,刻画的是函数的局部性质,而不是整体性质。f (x)< f (b) f (x)> f (a)概念深化:极大值与极小值 如图,找出函数y=f (x) 的极大值点和极小值点,同时说明y=f(x) 在这些点的导数值是多少? 注:极大值与极小值大小关系不能确定,且极值不唯一。f ?(a)=0f (x)> f (a)
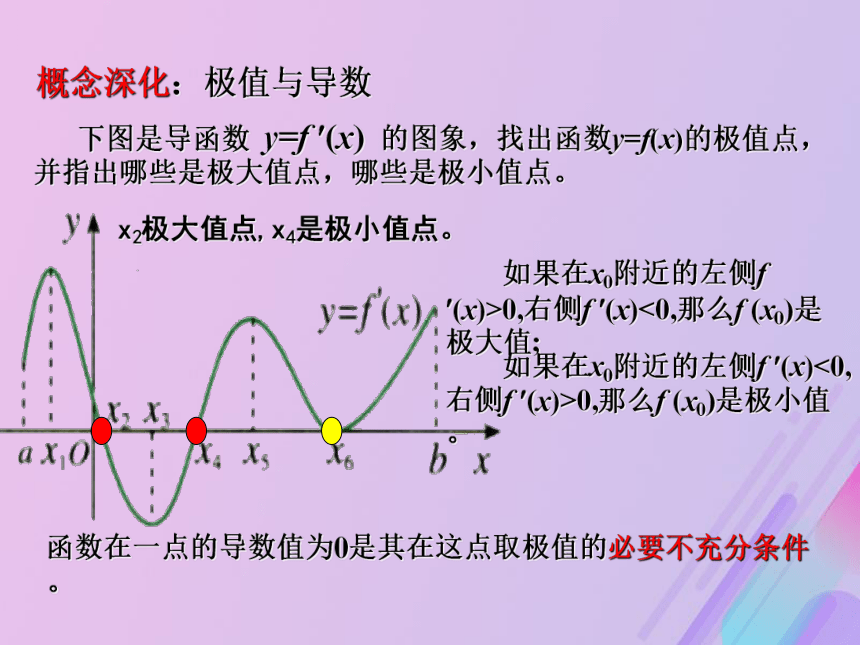
极小值f (x)< f (b) 极大值 下图是导函数 y=f ?(x) 的图象,找出函数y=f(x)的极值点,并指出哪些是极大值点,哪些是极小值点。x2极大值点,x4是极小值点。概念深化:极值与导数 如果在x0附近的左侧f ?(x)>0,右侧f ?(x)<0,那么f (x0)是极大值; 如果在x0附近的左侧f ?(x)<0,
右侧f ?(x)>0,那么f (x0)是极小值。函数在一点的导数值为0是其在这点取极值的必要不充分条件。解:例1得 x=2 或 x=-2当 f ?(x) > 0,得 x > 2 或 x < -2;例题分析当 f ?(x) < 0,得 -2 < x < 2 时。当x=-2时,f (x)有极大值,且当 x = 2时,f (x)有极小值,且总结:求函数y=f (x)的极值的步骤2、求方程f ?(x)=0的所有实数根; 左侧 f ?(a)=0 右侧
f ?(x)>0 极大值 f ?(x)<0
f ?(x)<0 极小值 f ?(x)>0 1、求导数f ?(x);3、利用导数求函数的单调区间(定义域);4、对每个实数根进行检验(列表法);课堂练习1求下列函数的极值找出f (x)的在区间[a,b]内极值和最值概念深化:极值与最值 对于非单调函数,把函数y=f (x)的所有极值与端点的函数值进行比较,从而得到函数的最大值和最小值。解: 例2 求函数 在区间[-3,4]
上的最大值和最小值。当 f ?(x) > 0,得 x > 2 或 x < -2;
当 f ?(x) < 0,得 -2 < x < 2 时。得 x=2, 或 x=-2所以,已知函数在区间[-3,4]上的最大是 ,最小值是 。例题分析总结:求函数y=f (x)闭区间上的最值的步骤2、求方程f ?(x)=0的所有实数根; 5、计算端点函数值;6、比较极值和端点的函数值,确定最值。1、求导数f ?(x);3、利用导数求函数的单调区间(定义域);4、对每个实数根进行检验(列表法),确定极值;求下列函数的最值课堂练习2课堂练习3 函数 在 处
有极大值,求常数 的值。课堂小结1.函数的极值与导数2.利用导数求函数极值的方法解方程f ?(x)=0.当f ?(x0)=0时(1)如果在x0附近的左侧f ?(x)>0,右侧f ?(x)<0,那么f (x0)是极大值;(2)如果在x0附近的左侧f ?(x)<0,右侧f ?(x)>0,那么f (x0)是极小值.函数在一点的导数值为0是其在
这点取极值的必要不充分条件。3.列表法求极值:4.函数在闭区间的最值 单调函数的最值在端点处取得;
非单调函数的最值在端点或极值点处取得,即把函数y=f (x)的所有极值与端点的函数值进行比较,从而得到函数的最大值和最小值。布置作业再见! 针对同学们所学内容的巩固与掌握,请认真完成:
如果f ?(x)>0,那么函数y=f (x)在这个区间内________;
如果f ?(x)<0,那么函数y=f (x)在这个区间内________.单调递增单调递减几何画板t=a点附近的图象有什么特点?导数的符号有什么变化规律?创设情景:跳水运动中高度随时间变化的函数图像t>at
导数符号有什么变化规律?概念形成:极值与极值点极小值点a和极大值点b统称为极值点,
极大值f (b)和极小值f (a)统称为极值。 注:极值点不是点,是取得极值时
自变量x的值,只能在开区间内取得。注: 极值反映函数在某一点附近的大小情况,刻画的是函数的局部性质,而不是整体性质。f (x)< f (b) f (x)> f (a)概念深化:极大值与极小值 如图,找出函数y=f (x) 的极大值点和极小值点,同时说明y=f(x) 在这些点的导数值是多少? 注:极大值与极小值大小关系不能确定,且极值不唯一。f ?(a)=0f (x)> f (a)
极小值f (x)< f (b) 极大值 下图是导函数 y=f ?(x) 的图象,找出函数y=f(x)的极值点,并指出哪些是极大值点,哪些是极小值点。x2极大值点,x4是极小值点。概念深化:极值与导数 如果在x0附近的左侧f ?(x)>0,右侧f ?(x)<0,那么f (x0)是极大值; 如果在x0附近的左侧f ?(x)<0,
右侧f ?(x)>0,那么f (x0)是极小值。函数在一点的导数值为0是其在这点取极值的必要不充分条件。解:例1得 x=2 或 x=-2当 f ?(x) > 0,得 x > 2 或 x < -2;例题分析当 f ?(x) < 0,得 -2 < x < 2 时。当x=-2时,f (x)有极大值,且当 x = 2时,f (x)有极小值,且总结:求函数y=f (x)的极值的步骤2、求方程f ?(x)=0的所有实数根; 左侧 f ?(a)=0 右侧
f ?(x)>0 极大值 f ?(x)<0
f ?(x)<0 极小值 f ?(x)>0 1、求导数f ?(x);3、利用导数求函数的单调区间(定义域);4、对每个实数根进行检验(列表法);课堂练习1求下列函数的极值找出f (x)的在区间[a,b]内极值和最值概念深化:极值与最值 对于非单调函数,把函数y=f (x)的所有极值与端点的函数值进行比较,从而得到函数的最大值和最小值。解: 例2 求函数 在区间[-3,4]
上的最大值和最小值。当 f ?(x) > 0,得 x > 2 或 x < -2;
当 f ?(x) < 0,得 -2 < x < 2 时。得 x=2, 或 x=-2所以,已知函数在区间[-3,4]上的最大是 ,最小值是 。例题分析总结:求函数y=f (x)闭区间上的最值的步骤2、求方程f ?(x)=0的所有实数根; 5、计算端点函数值;6、比较极值和端点的函数值,确定最值。1、求导数f ?(x);3、利用导数求函数的单调区间(定义域);4、对每个实数根进行检验(列表法),确定极值;求下列函数的最值课堂练习2课堂练习3 函数 在 处
有极大值,求常数 的值。课堂小结1.函数的极值与导数2.利用导数求函数极值的方法解方程f ?(x)=0.当f ?(x0)=0时(1)如果在x0附近的左侧f ?(x)>0,右侧f ?(x)<0,那么f (x0)是极大值;(2)如果在x0附近的左侧f ?(x)<0,右侧f ?(x)>0,那么f (x0)是极小值.函数在一点的导数值为0是其在
这点取极值的必要不充分条件。3.列表法求极值:4.函数在闭区间的最值 单调函数的最值在端点处取得;
非单调函数的最值在端点或极值点处取得,即把函数y=f (x)的所有极值与端点的函数值进行比较,从而得到函数的最大值和最小值。布置作业再见! 针对同学们所学内容的巩固与掌握,请认真完成:
