2018年高中数学第二章圆锥曲线与方程2.1.2由曲线求它的方程、由方程研究曲线的性质课件5新人教B版选修2_1(31张)
文档属性
| 名称 | 2018年高中数学第二章圆锥曲线与方程2.1.2由曲线求它的方程、由方程研究曲线的性质课件5新人教B版选修2_1(31张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 16:59:10 | ||
图片预览











文档简介
课件31张PPT。2.1.2 由曲线求它的方程、一、已知曲线求方程
1.求轨迹方程的一般步骤
(1)建系:建立适当的坐标系,用有序实数对(x,y)表示曲线上任意一点M的坐标.
(2)列式:写出适合条件P的点M的集合P={M|P(M)}.
(3)代换:用坐标表示条件P(M),列出方程f(x,y)=0.
(4)化简:化方程f(x,y)=0为最简形式.
(5)证明:说明以化简后方程的解为坐标的点都在曲线上.
可简记为:建系、列式、代换、化简、证明.注意:(1)求曲线方程以前,必须确定问题中的坐标系是否建立,若未建立,应先建系.建系是求曲线方程基础的一步,要根据几何关系适当建系,目的是简化求解过程且使曲线方程的形式简单.
(2)根据题目中的几何关系列出曲线上的点满足的坐标关系是关键一步,在这里常用到一些公式,如两点间距离公式、点到直线的距离公式、直线的斜率公式等,在化简过程中要保持等价变换,最后化为最简的方程形式.
(3)求曲线方程时步骤中的(2)、(5)两步一般可以省略,但应注意某些点的坐标是否适合方程,即要把多余的点剔除,将遗漏的点补上.
(4)求轨迹需要说明曲线类型,求轨迹方程则不必说明曲线类型.2.建立坐标系的基本原则
(1)让尽量多的点落在坐标轴上.
(2)尽可能地利用图形的对称性,使对称轴为坐标轴.
建立适当的坐标系是求曲线方程的首要一步,应充分利用图形的几何性质,如中心对称图形,可利用对称中心为原点建系;轴对称图形可利用对称轴为坐标轴建系;条件中有直角,可将两直角边作为坐标轴建系等.
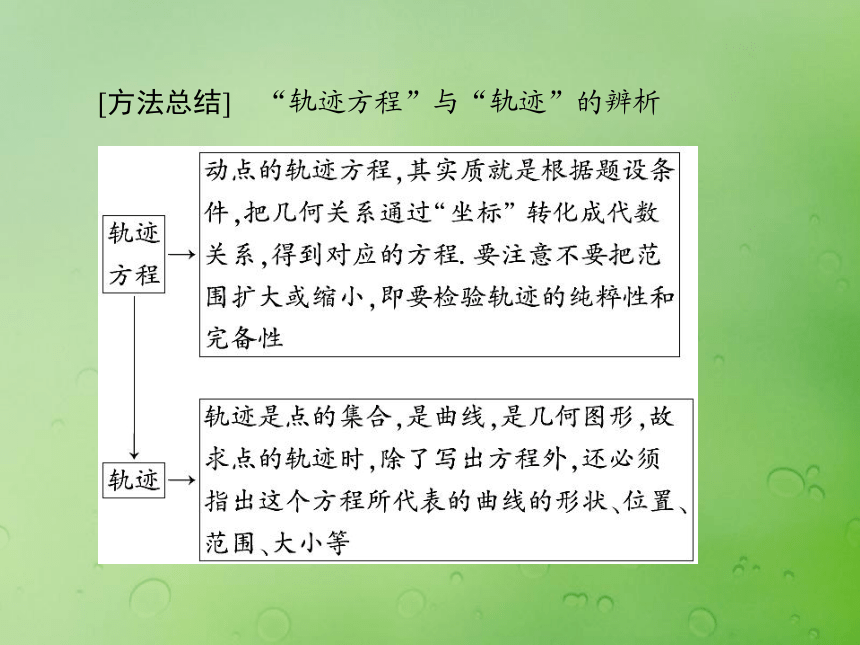
注意:坐标系选取的适当,可使运算过程简化,所得方程也较简单,否则,若坐标系选取不当,则会增加运算的繁杂程度.直接法求曲线方程 [方法总结] “轨迹方程”与“轨迹”的辨析已知点M到x轴的距离等于到y轴的距离的2倍,求点M的轨迹方程.
[解析] 设动点M的坐标为(x,y),则点M到x轴、y轴的距离分别为|y|,|x|.由题意知
|y|=2|x|,整理得y=±2x.
所以点M的轨迹方程为y=±2x. 用代入法或参数法求曲线方程 已知△ABC中,A(-2,0),B(0,-2),第三个顶点C在曲线y=3x2-1上移动,求△ABC重心的轨迹方程.
[思路分析] 重心坐标可直接设为(x,y),重心的变化是由顶点C的变化引起的,故只需找到两者之间的关系即可.即:x1=3x+2,
y1=3y+2.
又 (x1,y1)在曲线y=3x2-1上,即有y1=3x-1.
代入x1,y1,得:3y+2=3(3x+2)2-1.
化简得:y=9x2+12x+3即为所求轨迹方程.
[方法总结] 当已知某个动点在已知曲线上移动,而引起另一个动点的变化时,在求另一个动点满足的轨迹方程时,常用代入法.设定点M(-3,4),动点N在圆x2+y2=4上运动,以OM,ON为两边作平行四边形MONP,求点P的轨迹方程.用直接法或定义法求曲线方程 设圆C:(x-1)2+y2=1,过原点O作圆的任意弦,求所作弦的中点的轨迹方程.
[思路分析] 设P(x,y)为弦的中点,可用直接法列出关于x,y的方程,也可根据圆的性质判断出P点的轨迹,利用定义法求解.[方法总结] (1)适用定义法求轨迹的特点
如果动点的轨迹满足某种已知曲线的定义,则可依据定义写出轨迹方程.
(2)定义法求轨迹方程的策略
①要熟悉各种常见的曲线的定义.
②要善于利用数形结合的方法,利用图形具有的相关几何性质寻找等量关系.
③根据等量关系和曲线的定义确定动点的轨迹方程.(1)由动点P向圆x2+y2=1引两条切线PA,PB,切点分别为A,B,∠APB=60°,则动点P的轨迹方程为________.
(2)在Rt△ABC中,|AB|=2a(a>0),求直角顶点C的轨迹方程. 参数法求轨迹方程△ABC的顶点A固定,点A的对边BC的长是2a,边BC上的高是b,边BC沿一条定直线移动,求△ABC外心的轨迹方程.
[解析] 如图以BC所在定直线x轴,以过点A与x轴垂直的直线为y轴建立直角坐标系,则A点的坐标为(0,b).设△ABC的外心为M(x,y),作MN⊥BC于点N,则MN是BC的垂直平分线.三、常见的求轨迹方程的几种方法
1.直接法
当动点直接与已知条件发生联系时,在设曲线上动点的坐标为(x,y)后,可根据题设条件将普通语言运用基本公式(如两点间的距离公式、点到直线的距离公式、斜率公式、面积公式等)变换成表示动点坐标(x,y)间的关系式的数学语言,从而得到轨迹方程.这种求轨迹方程的方法称为直接法.直接法求轨迹方程经常要联系平面图形的性质.2.定义法
若动点运动的几何条件满足某种已知曲线的定义,可以设出其标准方程,然后用待定系数法求解,这种求轨迹方程的方法称为定义法.利用定义法求轨迹要善于抓住曲线的定义特征.
3.代入法(相关点法)
若所求轨迹上的动点P(x,y)与另一个已知曲线C:F(x,y)=0上的动点Q(x1,y1)存在着某种联系,可把点Q的坐标用点P的坐标表示出来,然后代入已知曲线C的方程F(x,y)=0,化简即得所求轨迹方程,这种求轨迹方程的方法叫做代入法(又称相关点法).
4.参数法
如果所求轨迹上的动点P(x,y)的坐标之间的关系不易找到,也没有相关信息可用时,可先考虑将x,y用一个或几个参数来表示,消去参数得轨迹方程,此法称为参数法.参数法中常选变角、变斜率等为参数.
1.求轨迹方程的一般步骤
(1)建系:建立适当的坐标系,用有序实数对(x,y)表示曲线上任意一点M的坐标.
(2)列式:写出适合条件P的点M的集合P={M|P(M)}.
(3)代换:用坐标表示条件P(M),列出方程f(x,y)=0.
(4)化简:化方程f(x,y)=0为最简形式.
(5)证明:说明以化简后方程的解为坐标的点都在曲线上.
可简记为:建系、列式、代换、化简、证明.注意:(1)求曲线方程以前,必须确定问题中的坐标系是否建立,若未建立,应先建系.建系是求曲线方程基础的一步,要根据几何关系适当建系,目的是简化求解过程且使曲线方程的形式简单.
(2)根据题目中的几何关系列出曲线上的点满足的坐标关系是关键一步,在这里常用到一些公式,如两点间距离公式、点到直线的距离公式、直线的斜率公式等,在化简过程中要保持等价变换,最后化为最简的方程形式.
(3)求曲线方程时步骤中的(2)、(5)两步一般可以省略,但应注意某些点的坐标是否适合方程,即要把多余的点剔除,将遗漏的点补上.
(4)求轨迹需要说明曲线类型,求轨迹方程则不必说明曲线类型.2.建立坐标系的基本原则
(1)让尽量多的点落在坐标轴上.
(2)尽可能地利用图形的对称性,使对称轴为坐标轴.
建立适当的坐标系是求曲线方程的首要一步,应充分利用图形的几何性质,如中心对称图形,可利用对称中心为原点建系;轴对称图形可利用对称轴为坐标轴建系;条件中有直角,可将两直角边作为坐标轴建系等.
注意:坐标系选取的适当,可使运算过程简化,所得方程也较简单,否则,若坐标系选取不当,则会增加运算的繁杂程度.直接法求曲线方程 [方法总结] “轨迹方程”与“轨迹”的辨析已知点M到x轴的距离等于到y轴的距离的2倍,求点M的轨迹方程.
[解析] 设动点M的坐标为(x,y),则点M到x轴、y轴的距离分别为|y|,|x|.由题意知
|y|=2|x|,整理得y=±2x.
所以点M的轨迹方程为y=±2x. 用代入法或参数法求曲线方程 已知△ABC中,A(-2,0),B(0,-2),第三个顶点C在曲线y=3x2-1上移动,求△ABC重心的轨迹方程.
[思路分析] 重心坐标可直接设为(x,y),重心的变化是由顶点C的变化引起的,故只需找到两者之间的关系即可.即:x1=3x+2,
y1=3y+2.
又 (x1,y1)在曲线y=3x2-1上,即有y1=3x-1.
代入x1,y1,得:3y+2=3(3x+2)2-1.
化简得:y=9x2+12x+3即为所求轨迹方程.
[方法总结] 当已知某个动点在已知曲线上移动,而引起另一个动点的变化时,在求另一个动点满足的轨迹方程时,常用代入法.设定点M(-3,4),动点N在圆x2+y2=4上运动,以OM,ON为两边作平行四边形MONP,求点P的轨迹方程.用直接法或定义法求曲线方程 设圆C:(x-1)2+y2=1,过原点O作圆的任意弦,求所作弦的中点的轨迹方程.
[思路分析] 设P(x,y)为弦的中点,可用直接法列出关于x,y的方程,也可根据圆的性质判断出P点的轨迹,利用定义法求解.[方法总结] (1)适用定义法求轨迹的特点
如果动点的轨迹满足某种已知曲线的定义,则可依据定义写出轨迹方程.
(2)定义法求轨迹方程的策略
①要熟悉各种常见的曲线的定义.
②要善于利用数形结合的方法,利用图形具有的相关几何性质寻找等量关系.
③根据等量关系和曲线的定义确定动点的轨迹方程.(1)由动点P向圆x2+y2=1引两条切线PA,PB,切点分别为A,B,∠APB=60°,则动点P的轨迹方程为________.
(2)在Rt△ABC中,|AB|=2a(a>0),求直角顶点C的轨迹方程. 参数法求轨迹方程△ABC的顶点A固定,点A的对边BC的长是2a,边BC上的高是b,边BC沿一条定直线移动,求△ABC外心的轨迹方程.
[解析] 如图以BC所在定直线x轴,以过点A与x轴垂直的直线为y轴建立直角坐标系,则A点的坐标为(0,b).设△ABC的外心为M(x,y),作MN⊥BC于点N,则MN是BC的垂直平分线.三、常见的求轨迹方程的几种方法
1.直接法
当动点直接与已知条件发生联系时,在设曲线上动点的坐标为(x,y)后,可根据题设条件将普通语言运用基本公式(如两点间的距离公式、点到直线的距离公式、斜率公式、面积公式等)变换成表示动点坐标(x,y)间的关系式的数学语言,从而得到轨迹方程.这种求轨迹方程的方法称为直接法.直接法求轨迹方程经常要联系平面图形的性质.2.定义法
若动点运动的几何条件满足某种已知曲线的定义,可以设出其标准方程,然后用待定系数法求解,这种求轨迹方程的方法称为定义法.利用定义法求轨迹要善于抓住曲线的定义特征.
3.代入法(相关点法)
若所求轨迹上的动点P(x,y)与另一个已知曲线C:F(x,y)=0上的动点Q(x1,y1)存在着某种联系,可把点Q的坐标用点P的坐标表示出来,然后代入已知曲线C的方程F(x,y)=0,化简即得所求轨迹方程,这种求轨迹方程的方法叫做代入法(又称相关点法).
4.参数法
如果所求轨迹上的动点P(x,y)的坐标之间的关系不易找到,也没有相关信息可用时,可先考虑将x,y用一个或几个参数来表示,消去参数得轨迹方程,此法称为参数法.参数法中常选变角、变斜率等为参数.
