2018年高中数学第二章圆锥曲线与方程2.2.1椭圆的标准方程课件6新人教B版选修2_1(23张)
文档属性
| 名称 | 2018年高中数学第二章圆锥曲线与方程2.2.1椭圆的标准方程课件6新人教B版选修2_1(23张) |  | |
| 格式 | zip | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 16:59:26 | ||
图片预览






文档简介
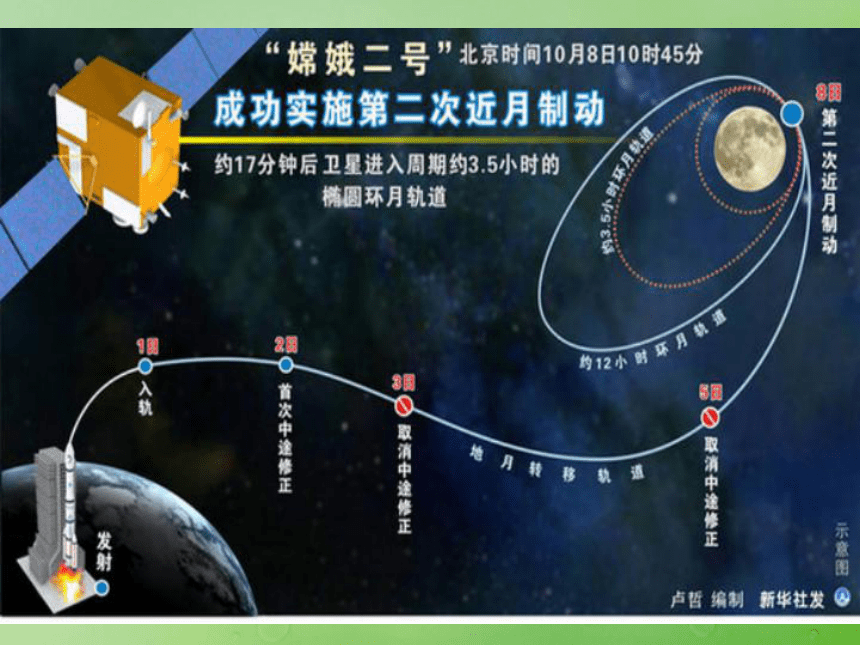
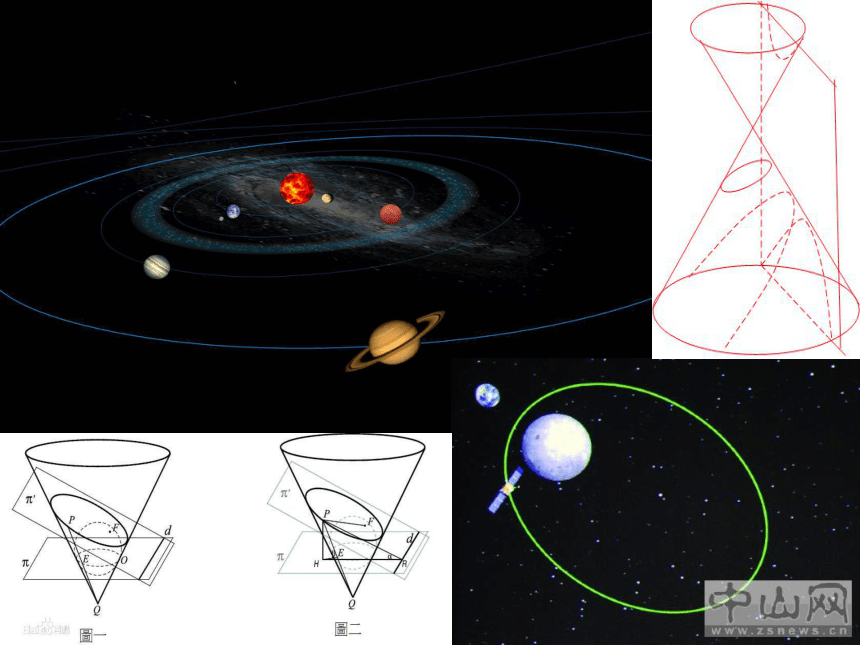
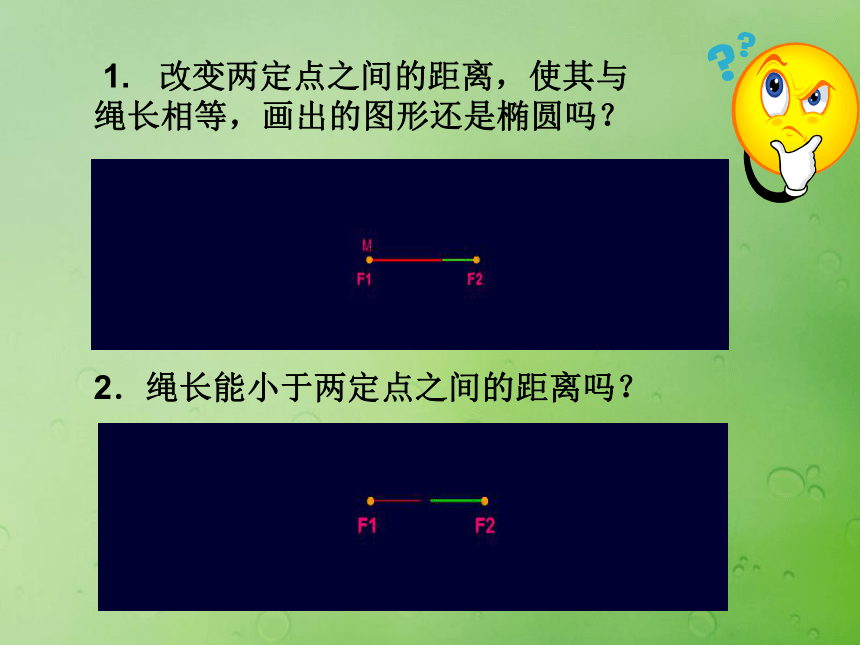
课件23张PPT。§2.2.1椭圆的标准方程?生活中、自然界处处存在着椭圆,我们如何用自己的双手画出椭圆呢? 1. 改变两定点之间的距离,使其与绳长相等,画出的图形还是椭圆吗?2.绳长能小于两定点之间的距离吗? 1. 改变两定点之间的距离,使其与绳长相等,画出的图形还是椭圆吗?2.绳长能小于两定点之间的距离吗? 椭圆的定义平面内与两个定点F1,F2的距离的和等于常数
(大于|F1F2|)的点的轨迹(或集合)叫椭圆。
这两个定点叫做椭圆的焦点。
两焦点的距离叫做椭圆的焦距。椭圆定义的文字表述:椭圆定义的符号表述:MF2F1结论:椭圆的定义需要注意以下几点1.平面内——这是大前提
2.动点M到两定点F1,F2的距离之和是常数2a
3.常数2a要大于焦距2C
结论: 1.当2a>2c时,点的轨迹为________
2.当2a=2c时,点的轨迹为________
3.当2a<2c时,点的轨迹_________ 椭圆不存在1.设动点M到两定点F1(-4,0), F2 (4,0)的距离和是10,
则动点M的轨迹为( )
2.设动点M到两定点F1(-4,0), F2 (4,0)的距离和是8,
则动点M的轨迹为( )
3.设动点M到两定点F1(-4,0), F2 (4,0)的距离和是a(正数),
则动点M的轨迹为( )
CBD练一练:(1)建系 求曲线方程的一般步骤是什么?(2)设点(3)找等量关系(4)列方程(5)化简(6)证明(检验)? 探讨建立平面直角坐标系的方案方案一原则:尽可能使方程的形式简单、运算简单;
(一般利用对称轴或已有的互相垂直的线段所在直线作为坐标轴.)(对称、“简洁”)解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图). 设M(x, y)是椭圆上任意一点,椭圆的焦距2c(c>0),M与F1和F2的距离的和等于常数2a (2a>2c) ,则F1、F2的坐标分别是(?c,0)、(c,0) .(探究:下面怎样化简?)由椭圆的定义得:代入坐标椭圆标准方程的推导 总体印象:对称、简洁,“像”直线方程的截距式焦点在y轴:焦点在x轴:椭圆的标准方程哪个分母大,焦点就在哪个轴上平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹?再认识!例1 已知椭圆的两个焦点的坐标分别是
(-4,0),(4,0)椭圆上一点到两焦
点距离的和等于10,求椭圆的标准方程.
变式:已知椭圆的焦距等于8,椭圆上一点到两
焦点距离的和等于10,求椭圆的标准方程解:由题意容易知2c=8,2a=10,得c=4,
a=5故b2=a2-c2=9,但焦点未定,
所以标准方程有两个:或 因为椭圆的焦点在y轴上所以椭圆的标准方程为:解法一:由椭圆的定义知:定义法例2: 已知椭圆的两个焦点的坐标分别是 (0 ,-2)
(0 ,2)并且经过点 求椭圆的标准方程.F2练习1.下列方程哪些表示椭圆? 若是,则判定其焦点在何轴?
并指明 ,写出焦点坐标.?所以所求椭圆的标准方程为:解法二:设所求的标准方程为解得:待定系数法例2: 已知椭圆的两个焦点的坐标分别是 (0 ,-2)
(0 ,2)并且经过点 求椭圆的标准方程.想一想
本节课你有什么收获?1、知识方面
(1)椭圆的定义;
2、数学思想及方法:
数形结合的思想、转化思想及坐标法。(2)椭圆的两种标准方程及联系;(3) 椭圆方程的求法:定义法和待定系数法感谢各位领导老师莅临指导!同学们,下课啦!
(大于|F1F2|)的点的轨迹(或集合)叫椭圆。
这两个定点叫做椭圆的焦点。
两焦点的距离叫做椭圆的焦距。椭圆定义的文字表述:椭圆定义的符号表述:MF2F1结论:椭圆的定义需要注意以下几点1.平面内——这是大前提
2.动点M到两定点F1,F2的距离之和是常数2a
3.常数2a要大于焦距2C
结论: 1.当2a>2c时,点的轨迹为________
2.当2a=2c时,点的轨迹为________
3.当2a<2c时,点的轨迹_________ 椭圆不存在1.设动点M到两定点F1(-4,0), F2 (4,0)的距离和是10,
则动点M的轨迹为( )
2.设动点M到两定点F1(-4,0), F2 (4,0)的距离和是8,
则动点M的轨迹为( )
3.设动点M到两定点F1(-4,0), F2 (4,0)的距离和是a(正数),
则动点M的轨迹为( )
CBD练一练:(1)建系 求曲线方程的一般步骤是什么?(2)设点(3)找等量关系(4)列方程(5)化简(6)证明(检验)? 探讨建立平面直角坐标系的方案方案一原则:尽可能使方程的形式简单、运算简单;
(一般利用对称轴或已有的互相垂直的线段所在直线作为坐标轴.)(对称、“简洁”)解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图). 设M(x, y)是椭圆上任意一点,椭圆的焦距2c(c>0),M与F1和F2的距离的和等于常数2a (2a>2c) ,则F1、F2的坐标分别是(?c,0)、(c,0) .(探究:下面怎样化简?)由椭圆的定义得:代入坐标椭圆标准方程的推导 总体印象:对称、简洁,“像”直线方程的截距式焦点在y轴:焦点在x轴:椭圆的标准方程哪个分母大,焦点就在哪个轴上平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹?再认识!例1 已知椭圆的两个焦点的坐标分别是
(-4,0),(4,0)椭圆上一点到两焦
点距离的和等于10,求椭圆的标准方程.
变式:已知椭圆的焦距等于8,椭圆上一点到两
焦点距离的和等于10,求椭圆的标准方程解:由题意容易知2c=8,2a=10,得c=4,
a=5故b2=a2-c2=9,但焦点未定,
所以标准方程有两个:或 因为椭圆的焦点在y轴上所以椭圆的标准方程为:解法一:由椭圆的定义知:定义法例2: 已知椭圆的两个焦点的坐标分别是 (0 ,-2)
(0 ,2)并且经过点 求椭圆的标准方程.F2练习1.下列方程哪些表示椭圆? 若是,则判定其焦点在何轴?
并指明 ,写出焦点坐标.?所以所求椭圆的标准方程为:解法二:设所求的标准方程为解得:待定系数法例2: 已知椭圆的两个焦点的坐标分别是 (0 ,-2)
(0 ,2)并且经过点 求椭圆的标准方程.想一想
本节课你有什么收获?1、知识方面
(1)椭圆的定义;
2、数学思想及方法:
数形结合的思想、转化思想及坐标法。(2)椭圆的两种标准方程及联系;(3) 椭圆方程的求法:定义法和待定系数法感谢各位领导老师莅临指导!同学们,下课啦!
