2018年高中数学第二章圆锥曲线与方程2.3.1双曲线的标准方程课件6新人教B版选修2_1(17张)
文档属性
| 名称 | 2018年高中数学第二章圆锥曲线与方程2.3.1双曲线的标准方程课件6新人教B版选修2_1(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 00:00:00 | ||
图片预览




文档简介
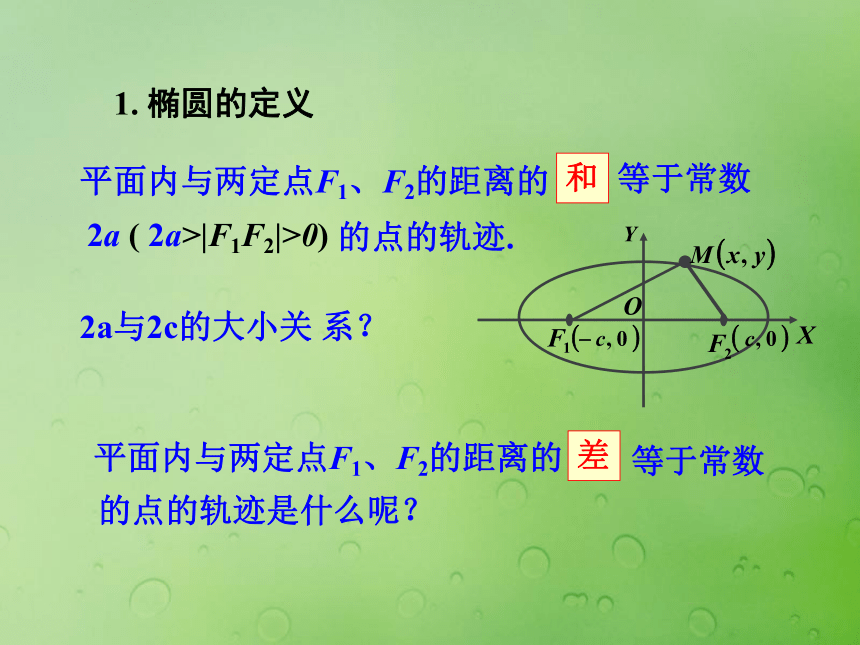
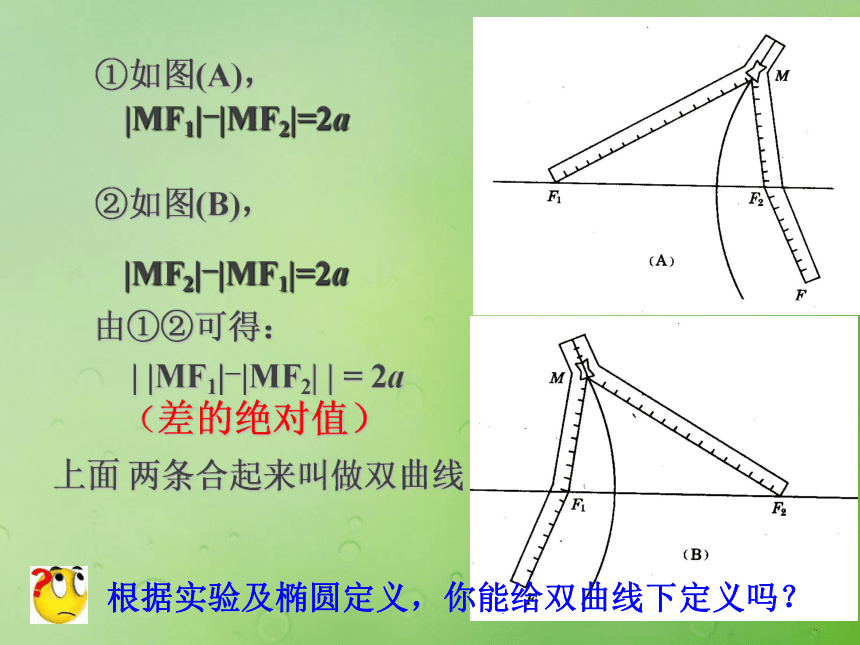
课件17张PPT。双曲线及其标准方程 巴西利亚大教堂北京摩天大楼法拉利主题公园花瓶1. 椭圆的定义2a与2c的大小关 系?①如图(A), |MF1|-|MF2|=2a②如图(B),上面 两条合起来叫做双曲线由①②可得: | |MF1|-|MF2| | = 2a
(差的绝对值) |MF2|-|MF1|=2a根据实验及椭圆定义,你能给双曲线下定义吗? 平面内与两个定点F1,F2的距离的和为一个定值(大于︱F1F2︱ )的点的轨迹叫做椭圆 平面内与两个定点F1,F2的距离的差的绝对值
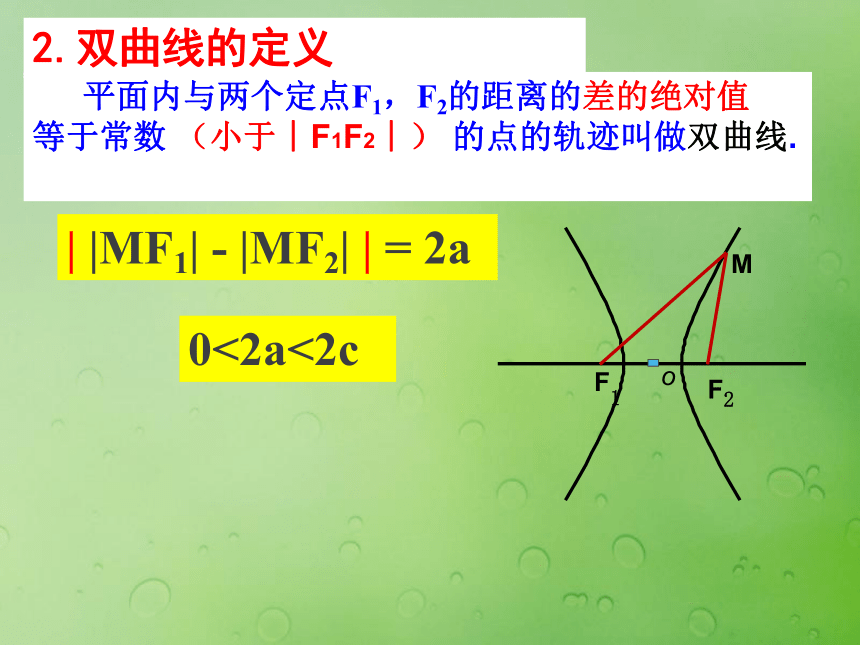
等于常数 (小于︱F1F2︱) 的点的轨迹叫做双曲线.
| |MF1| - |MF2| | = 2a0<2a<2c2.双曲线的定义点的轨迹为两条射线F1P、F2Q。②常数2a>2c时①常数2a=2c时M③常数2a=0时xyo 设M(x , y),双曲线的焦
距为2c(c>0),F1(-c,0),F2(c,0)F1F2M 以F1,F2所在的直线为X轴,线段F1F2的中点为原点建立直角坐标系1. 建系.2.设点.4.化简.3.双曲线的标准方程令c2-a2=b2yoF1M双曲线定义及标准方程| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)F ( ±c, 0) F (0, ± c)双曲线定义及标准方程| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)F ( ±c, 0) F (0, ± c)判断: 与 的焦点位置?思考:如何由双曲线的标准方程来判断它的焦点
是在X轴上还是Y轴上?结论:看 前的系数,哪一个为正,则焦点在哪一个轴上。例1.已知双曲线的焦点为F1(-5,0), F2(5,0)双曲线上一点到两焦点的距离差的绝对值等于6,则
(1) a=_______ , c =_______ , b =_______
(2) 双曲线的标准方程为______________(4)双曲线上一点P, |PF1|=10, 则|PF2|=_________3544或16例题分析 (3)若两定点改为|F1F2|=10,则轨迹方程
为______________练习1:求双曲线的标准方程。(1)(2)(3)焦点在x轴上,经过点例2:如果方程 表示双曲线,
求m的取值范围.变式:已知方程方程表示椭圆,则K的取值范围是_______方程表示双曲线,则K的取值范围是_____上题的椭圆与双曲线的一个交点为P,
焦点为F1,F2,求|PF1|.变式:系数哪个为正,焦点就在哪个轴上平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于|F1F2 | )的点的轨迹根据所学知识完成下表c2-a2=b2y
(差的绝对值) |MF2|-|MF1|=2a根据实验及椭圆定义,你能给双曲线下定义吗? 平面内与两个定点F1,F2的距离的和为一个定值(大于︱F1F2︱ )的点的轨迹叫做椭圆 平面内与两个定点F1,F2的距离的差的绝对值
等于常数 (小于︱F1F2︱) 的点的轨迹叫做双曲线.
| |MF1| - |MF2| | = 2a0<2a<2c2.双曲线的定义点的轨迹为两条射线F1P、F2Q。②常数2a>2c时①常数2a=2c时M③常数2a=0时xyo 设M(x , y),双曲线的焦
距为2c(c>0),F1(-c,0),F2(c,0)F1F2M 以F1,F2所在的直线为X轴,线段F1F2的中点为原点建立直角坐标系1. 建系.2.设点.4.化简.3.双曲线的标准方程令c2-a2=b2yoF1M双曲线定义及标准方程| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)F ( ±c, 0) F (0, ± c)双曲线定义及标准方程| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)F ( ±c, 0) F (0, ± c)判断: 与 的焦点位置?思考:如何由双曲线的标准方程来判断它的焦点
是在X轴上还是Y轴上?结论:看 前的系数,哪一个为正,则焦点在哪一个轴上。例1.已知双曲线的焦点为F1(-5,0), F2(5,0)双曲线上一点到两焦点的距离差的绝对值等于6,则
(1) a=_______ , c =_______ , b =_______
(2) 双曲线的标准方程为______________(4)双曲线上一点P, |PF1|=10, 则|PF2|=_________3544或16例题分析 (3)若两定点改为|F1F2|=10,则轨迹方程
为______________练习1:求双曲线的标准方程。(1)(2)(3)焦点在x轴上,经过点例2:如果方程 表示双曲线,
求m的取值范围.变式:已知方程方程表示椭圆,则K的取值范围是_______方程表示双曲线,则K的取值范围是_____上题的椭圆与双曲线的一个交点为P,
焦点为F1,F2,求|PF1|.变式:系数哪个为正,焦点就在哪个轴上平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于|F1F2 | )的点的轨迹根据所学知识完成下表c2-a2=b2y
