2018年高中数学第二章圆锥曲线与方程2.3.2双曲线的几何性质课件7新人教B版选修2_1(18张)
文档属性
| 名称 | 2018年高中数学第二章圆锥曲线与方程2.3.2双曲线的几何性质课件7新人教B版选修2_1(18张) |  | |
| 格式 | zip | ||
| 文件大小 | 892.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 17:00:43 | ||
图片预览




文档简介
课件18张PPT。课题:双曲线的几何性质
1.类比椭圆学习双曲线的几何性质,并能据此解决一些简单问题
2.体会类比的学习方法,以及数形结合思想的运用
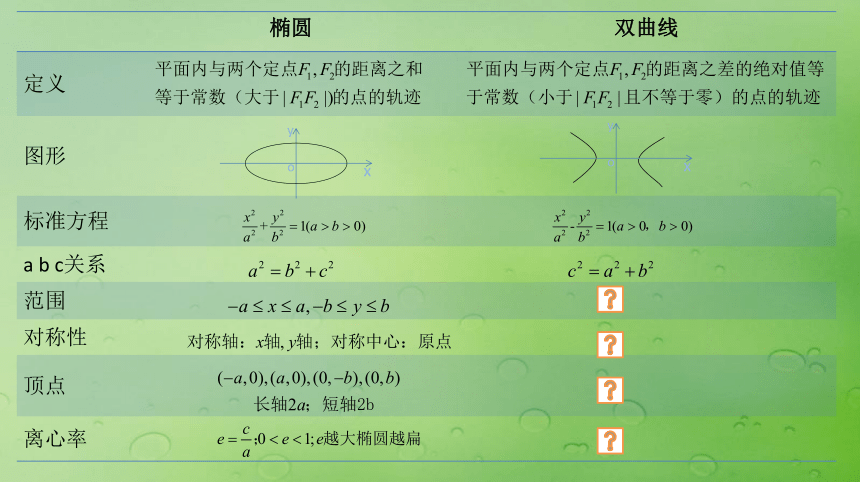
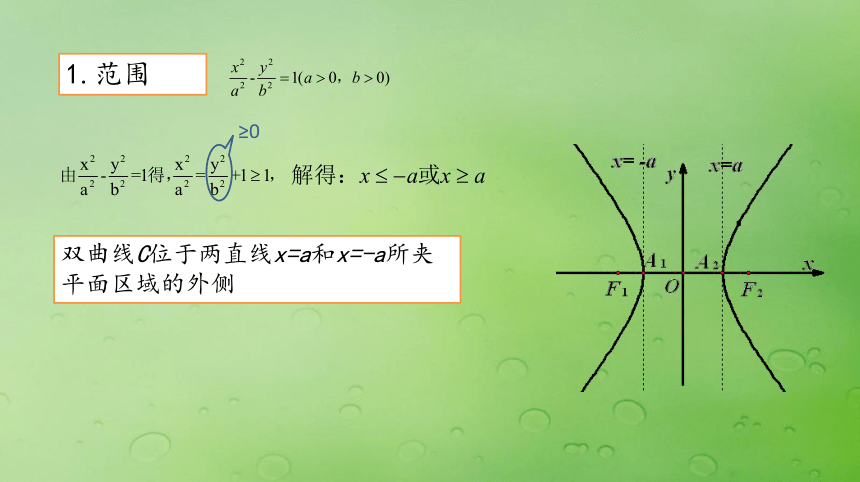
3.发现圆锥曲线在现实中的应用价值,增强学习兴趣xyoxyo1.范围双曲线C位于两直线x=a和x=-a所夹平面区域的外侧≥02.对称性用-X代替X,方程不变,双曲线关于y轴对称;
用-y代替y,方程不变,双曲线关于x轴对称;
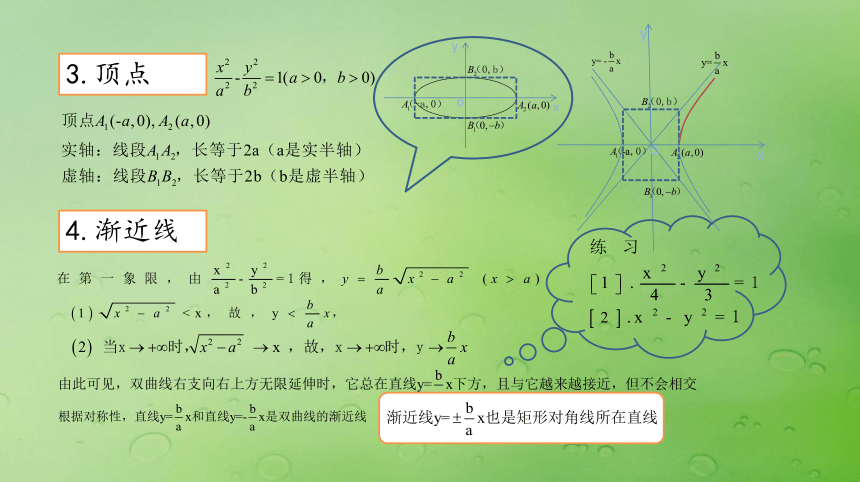
同时用-x,-y代替x,y,方程不变,双曲线关于原点对称双曲线是以x轴,y轴为对称轴的轴对称图形;也是以原点为对称中心的中心对称图形。这个对称中心叫做双曲线的中心3.顶点oyxxoy4.渐近线5.离心率且e>1oyx?abc题型一 已知双曲线的标准方程求其几何性质(正用)
例1 求双曲线16x2-9y2=144的顶点坐标、焦点坐标、实轴长、虚轴长、离心率、渐近线方程.注:化标,定型典例导析变式训练 求双曲线 x2-3y2+12=0的实轴长、虚轴长、焦点坐标、顶点坐标、渐近线方程、离心率.题型二 根据双曲线的几何性质求标准方程(逆用)
例2 已知双曲线的焦点在X轴上,中心在原点,如果焦距为8,实轴长为6,求此双曲线的标准方程及其离心率当堂检测能力提升能力提升2.双曲线mx2+y2=1的虚轴长是实轴长的2倍,则m的值为________.解析 由双曲线方程mx2+y2=1,知m<0,能力提升课堂小结oyx类比学习的方法
1.类比椭圆学习双曲线的几何性质,并能据此解决一些简单问题
2.体会类比的学习方法,以及数形结合思想的运用
3.发现圆锥曲线在现实中的应用价值,增强学习兴趣xyoxyo1.范围双曲线C位于两直线x=a和x=-a所夹平面区域的外侧≥02.对称性用-X代替X,方程不变,双曲线关于y轴对称;
用-y代替y,方程不变,双曲线关于x轴对称;
同时用-x,-y代替x,y,方程不变,双曲线关于原点对称双曲线是以x轴,y轴为对称轴的轴对称图形;也是以原点为对称中心的中心对称图形。这个对称中心叫做双曲线的中心3.顶点oyxxoy4.渐近线5.离心率且e>1oyx?abc题型一 已知双曲线的标准方程求其几何性质(正用)
例1 求双曲线16x2-9y2=144的顶点坐标、焦点坐标、实轴长、虚轴长、离心率、渐近线方程.注:化标,定型典例导析变式训练 求双曲线 x2-3y2+12=0的实轴长、虚轴长、焦点坐标、顶点坐标、渐近线方程、离心率.题型二 根据双曲线的几何性质求标准方程(逆用)
例2 已知双曲线的焦点在X轴上,中心在原点,如果焦距为8,实轴长为6,求此双曲线的标准方程及其离心率当堂检测能力提升能力提升2.双曲线mx2+y2=1的虚轴长是实轴长的2倍,则m的值为________.解析 由双曲线方程mx2+y2=1,知m<0,能力提升课堂小结oyx类比学习的方法
