2018年高中数学第二章圆锥曲线与方程2.4.2抛物线的几何性质课件6新人教B版选修2_1(15张)
文档属性
| 名称 | 2018年高中数学第二章圆锥曲线与方程2.4.2抛物线的几何性质课件6新人教B版选修2_1(15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 367.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 00:00:00 | ||
图片预览



文档简介
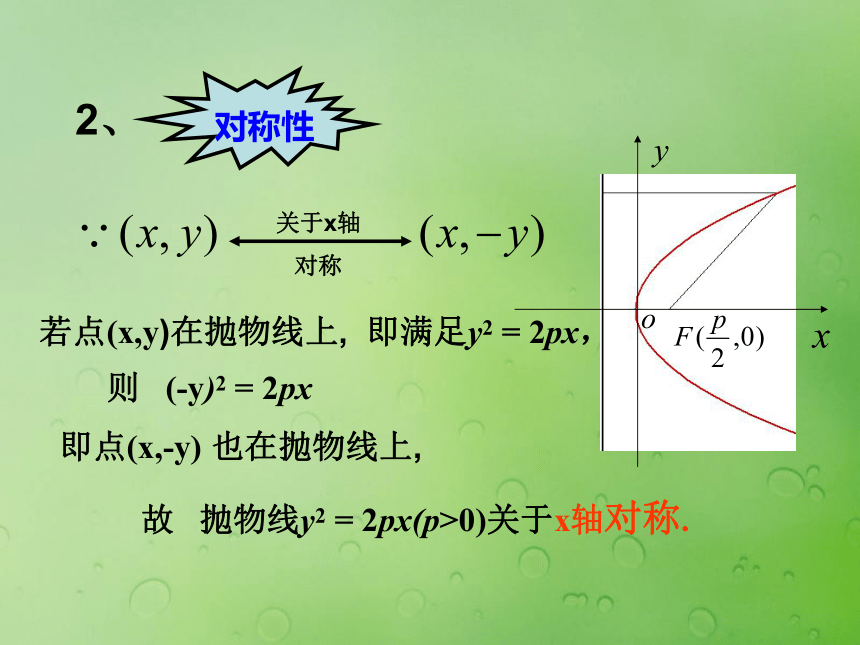
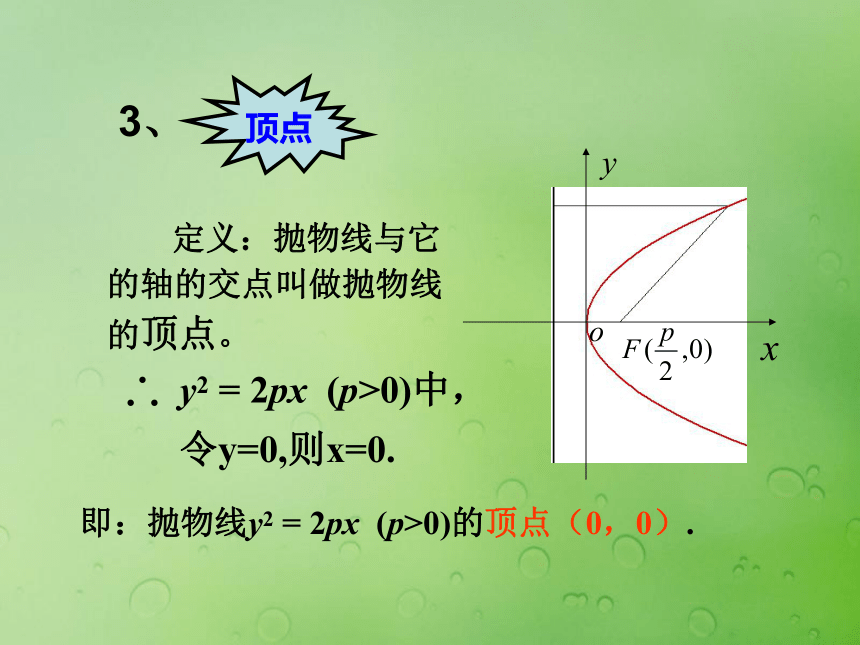
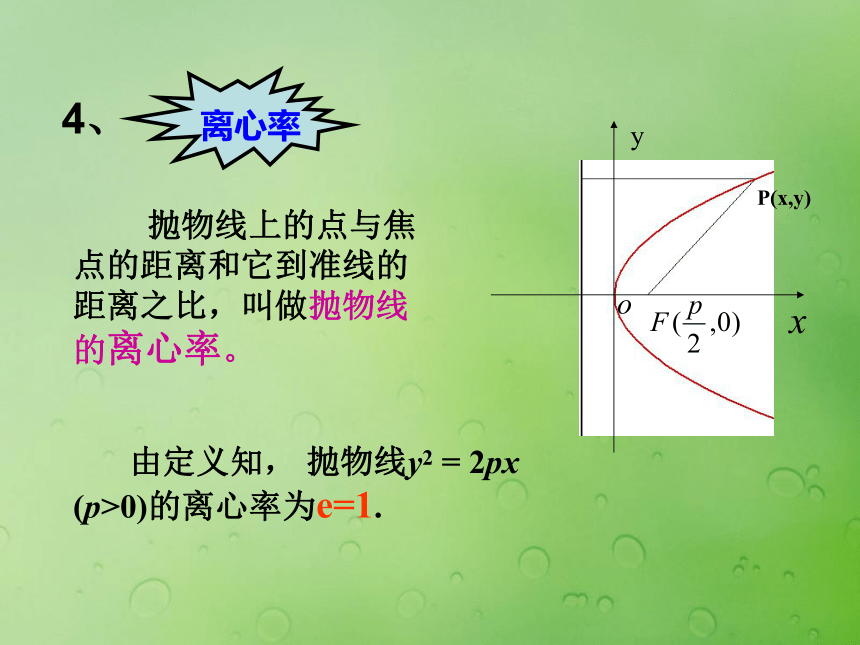
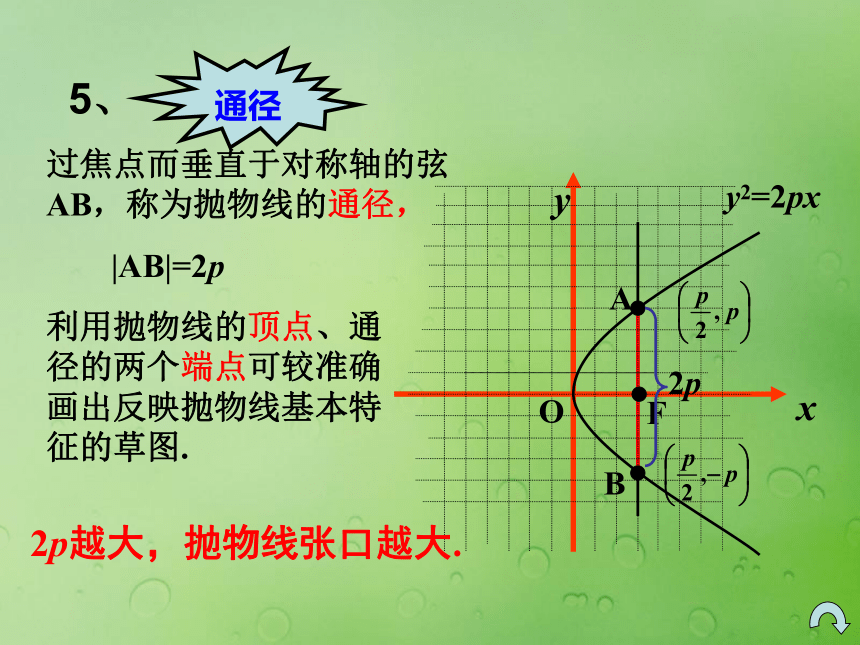
课件15张PPT。2.4.2抛物线的简单几何性质(1)一、温故知新(一) 圆锥曲线的统一定义 平面内,到定点F的距离与到定直线l的距离比为常数e的点的轨迹,当e>1时,是双曲线 .当00)(2)开口向左y2 = -2px (p>0)(3)开口向上x2 = 2py (p>0)(4)开口向下x2 = -2py (p>0)(三) 抛物线的标准方程由抛物线y2 =2px(p>0)二、探索新知如何研究抛物线y2 =2px(p>0)的几何性质?思考:y的范围呢?即点(x,-y) 也在抛物线上,故 抛物线y2 = 2px(p>0)关于x轴对称.则 (-y)2 = 2px若点(x,y)在抛物线上, 即满足y2 = 2px, 定义:抛物线与它的轴的交点叫做抛物线的顶点。即:抛物线y2 = 2px (p>0)的顶点(0,0). 抛物线上的点与焦点的距离和它到准线的距离之比,叫做抛物线的离心率。 由定义知, 抛物线y2 = 2px (p>0)的离心率为e=1.FABy2=2px2p过焦点而垂直于对称轴的弦AB,称为抛物线的通径,利用抛物线的顶点、通径的两个端点可较准确画出反映抛物线基本特征的草图.|AB|=2p2p越大,抛物线张口越大.连接抛物线任意一点与焦点的线段叫做抛物线的焦半径。|PF|=x0+p/2(同学们推另三种情况)焦半径公式:F归纳:
(1)、抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但没有渐近线;
(2)、抛物线只有一条对称轴,没有对称中心;
(3)、抛物线只有一个顶点,一个焦点,一条准线;
(4)、抛物线的离心率e是确定的为1,
⑸、抛物线的通径为2P, 2p越大,抛物线的张口越大.
解:三、典例精析探照灯、汽车前灯的反光曲面,手电筒的反光镜面、太阳灶的镜面都是抛物镜面。抛物镜面:抛物线绕其对称轴旋转而成的曲面。灯泡放在抛物线的焦点位置上,通过镜面反射就变
成了平行光束,这就是探照灯、汽车前灯、手电筒的
设计原理。平行光线射到抛物镜面上,经镜面反射后,反射光线都
经过抛物线的焦点,这就是太阳灶能把光能转化为热能
的理论依据。例2:探照灯反射镜的轴截面是抛物线的一部分,光源
位于抛物线的焦点处。已知灯口圆的直径为60cm,灯深
40cm,求抛物线的标准方程和焦点位置。解:设抛物线的标准方程为:y2=2px由条件可得A (40,30),代入方程得:302=2p·40 (1)已知点A(-2,3)与抛物线 的焦点
的距离是5,则P = 。 (2)抛物线 的弦AB垂直x轴,若|AB|= ,
则焦点到AB的距离为 。 42(3)已知直线x-y=2与抛物线 交于A、B两
点,那么线段AB的中点坐标是 。 四、课堂练习(4)求焦点在直线x-2y-4=0上的抛物线的标准方程.(5)点A的坐标为(3,1),若P是抛物线 上的一动
点,F是抛物线的焦点,则|PA|+|PF|的最小值为( )
(A) 3 (B) 4 (C) 5 (D) 6B 五、归纳总结抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但没有渐近线;抛物线只有一条对称轴,没有对称中心;抛物线的离心率是确定的,e=1;抛物线只有一个顶点,一个焦点,一条准线;抛物线的通径为2P, 2p越大,抛物线的张口越大.1、范围:2、对称性:3、顶点:4、离心率:5、通径:6、焦半径:从焦点出发的光线,通过抛物线反射就变成了平行光束.7、光学性质:|PF|=x0+p/2(同学们已推出另三种情况)再见!
(1)、抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但没有渐近线;
(2)、抛物线只有一条对称轴,没有对称中心;
(3)、抛物线只有一个顶点,一个焦点,一条准线;
(4)、抛物线的离心率e是确定的为1,
⑸、抛物线的通径为2P, 2p越大,抛物线的张口越大.
解:三、典例精析探照灯、汽车前灯的反光曲面,手电筒的反光镜面、太阳灶的镜面都是抛物镜面。抛物镜面:抛物线绕其对称轴旋转而成的曲面。灯泡放在抛物线的焦点位置上,通过镜面反射就变
成了平行光束,这就是探照灯、汽车前灯、手电筒的
设计原理。平行光线射到抛物镜面上,经镜面反射后,反射光线都
经过抛物线的焦点,这就是太阳灶能把光能转化为热能
的理论依据。例2:探照灯反射镜的轴截面是抛物线的一部分,光源
位于抛物线的焦点处。已知灯口圆的直径为60cm,灯深
40cm,求抛物线的标准方程和焦点位置。解:设抛物线的标准方程为:y2=2px由条件可得A (40,30),代入方程得:302=2p·40 (1)已知点A(-2,3)与抛物线 的焦点
的距离是5,则P = 。 (2)抛物线 的弦AB垂直x轴,若|AB|= ,
则焦点到AB的距离为 。 42(3)已知直线x-y=2与抛物线 交于A、B两
点,那么线段AB的中点坐标是 。 四、课堂练习(4)求焦点在直线x-2y-4=0上的抛物线的标准方程.(5)点A的坐标为(3,1),若P是抛物线 上的一动
点,F是抛物线的焦点,则|PA|+|PF|的最小值为( )
(A) 3 (B) 4 (C) 5 (D) 6B 五、归纳总结抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但没有渐近线;抛物线只有一条对称轴,没有对称中心;抛物线的离心率是确定的,e=1;抛物线只有一个顶点,一个焦点,一条准线;抛物线的通径为2P, 2p越大,抛物线的张口越大.1、范围:2、对称性:3、顶点:4、离心率:5、通径:6、焦半径:从焦点出发的光线,通过抛物线反射就变成了平行光束.7、光学性质:|PF|=x0+p/2(同学们已推出另三种情况)再见!
