2018年高中数学第三章空间向量与立体几何3.2.4二面角及其度量课件5新人教B版选修2_1(34张)
文档属性
| 名称 | 2018年高中数学第三章空间向量与立体几何3.2.4二面角及其度量课件5新人教B版选修2_1(34张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 701.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 00:00:00 | ||
图片预览






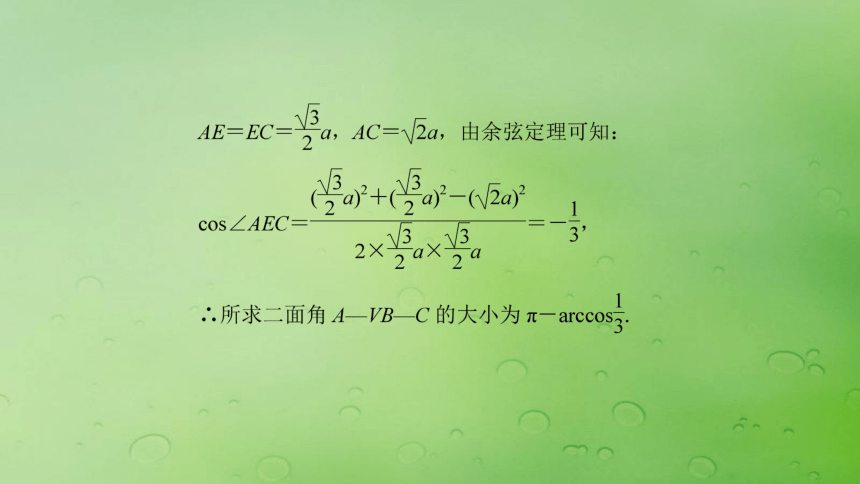



文档简介
(共34张PPT)
3.2.4 二面角及其度量
1.知识与技能
掌握二面角的有关概念.
能够求二面角的大小.
2.过程与方法
通过二面角的平面角的空间模型,培养空间想象能力.
3.情感态度与价值观
建立学习空间向量的自信心、培养学习数学的兴趣.
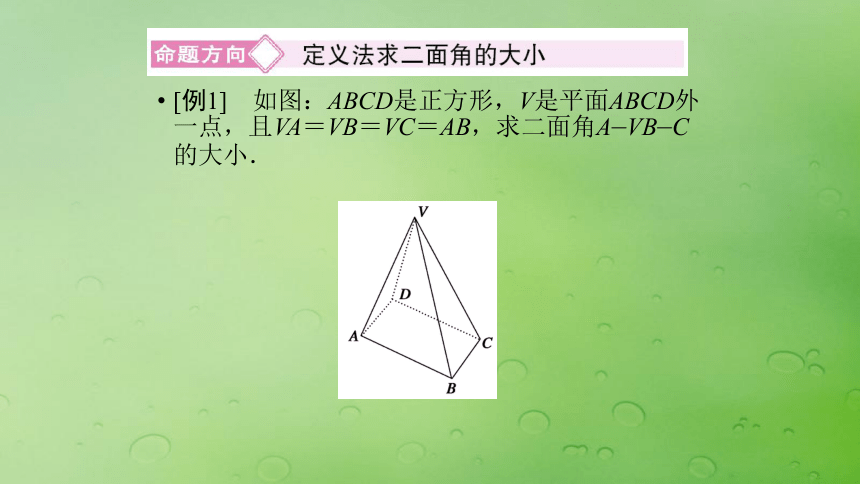
[例1] 如图:ABCD是正方形,V是平面ABCD外一点,且VA=VB=VC=AB,求二面角A—VB—C的大小.
[说明] (1)所谓定义法,就是在二面角的棱上取一适当点作出平面角,然后解三角形即可(或者作(找)一个与棱垂直的平面,与两面的交线构成的角).
(2)求二面角的步骤:
①作(找)出二面角的平面角;
②写出(或证明)所作平面角即为所求二面角的平面角;
③利用解三角形的知识求解.
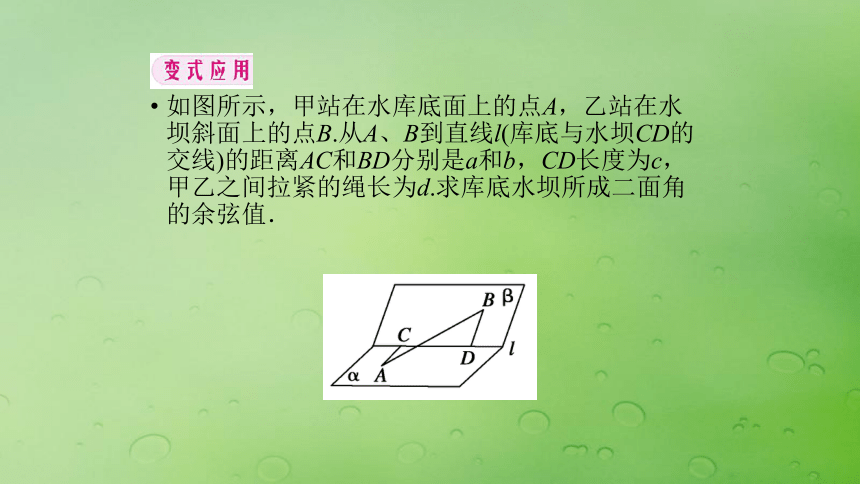
如图所示,甲站在水库底面上的点A,乙站在水坝斜面上的点B.从A、B到直线l(库底与水坝CD的交线)的距离AC和BD分别是a和b,CD长度为c,甲乙之间拉紧的绳长为d.求库底水坝所成二面角的余弦值.
1
向量都指向二面角外或内方向
π-θ
π-θ
θ
θ
2
法向量一个指向内一个指向外
θ
θ
θ
θ
[例2] 如图,四棱锥P—ABCD中,PA⊥底面ABCD.底面ABCD为边长是1的正方形,PA=1,求平面PCD与平面PAB夹角的大小.
[分析] 解答本题可首先求出平面PCD和平面PAB的法向量,再求其夹角大小,然后转化为平面PCD与平面PAB夹角的大小.
在本例中求二面角A—PB—D的大小.
3用公式cosθ=S′S,其中S′为射影面积,S为原图形面积.
[解析] ∵∠SAB=∠SAC=90°,
∴SA⊥面ABC.
∴AC为SC在底面ABC上的射影.
又∠ACB=90°,
∴SC⊥BC.
∴∠SCA为二面角S—BC—A的平面角.
一、选择题
1.设直线l的方向向量为a,平面α的法向量为b,若a·b=0,则 ( )
A.l∥α B.l α
C.l⊥α D.l α或l∥α
[答案] D
[解析] 因为a·b=0,所以a⊥b,故选D.
2.正方形ABCD所在平面外一点P,PA⊥平面ABCD,若PA=AB,则平面PAB与平面PCD所成的角的度数为( )
A.30° B.45°
C.60° D.90°
[答案] B
[解析] ∠DPA为二面角平面角,而在Rt△PAD内,∠APD=45°.故选B.
3.如图正方体ABCD-A1B1C1D1中,E、F分别是BB1和DD1的中点,则平面ECF与平面ABCD的夹角的余弦值为( )
[答案] B
二、填空题
4.正方体AC1中平面ABCD与平面A1BCD1的夹角为________.
[答案] 45°
[解析] ∠A1BA为平面角.
5 正三角形ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A—DC—B(如图②).在图②中求平面ABD与平面EFD所成二面角.
[辨析] 求二面角大小,一要注意准确计算,二要注意观察二面角是锐角还是钝角,以确定求出来的余弦值是正还是负.
3.2.4 二面角及其度量
1.知识与技能
掌握二面角的有关概念.
能够求二面角的大小.
2.过程与方法
通过二面角的平面角的空间模型,培养空间想象能力.
3.情感态度与价值观
建立学习空间向量的自信心、培养学习数学的兴趣.
[例1] 如图:ABCD是正方形,V是平面ABCD外一点,且VA=VB=VC=AB,求二面角A—VB—C的大小.
[说明] (1)所谓定义法,就是在二面角的棱上取一适当点作出平面角,然后解三角形即可(或者作(找)一个与棱垂直的平面,与两面的交线构成的角).
(2)求二面角的步骤:
①作(找)出二面角的平面角;
②写出(或证明)所作平面角即为所求二面角的平面角;
③利用解三角形的知识求解.
如图所示,甲站在水库底面上的点A,乙站在水坝斜面上的点B.从A、B到直线l(库底与水坝CD的交线)的距离AC和BD分别是a和b,CD长度为c,甲乙之间拉紧的绳长为d.求库底水坝所成二面角的余弦值.
1
向量都指向二面角外或内方向
π-θ
π-θ
θ
θ
2
法向量一个指向内一个指向外
θ
θ
θ
θ
[例2] 如图,四棱锥P—ABCD中,PA⊥底面ABCD.底面ABCD为边长是1的正方形,PA=1,求平面PCD与平面PAB夹角的大小.
[分析] 解答本题可首先求出平面PCD和平面PAB的法向量,再求其夹角大小,然后转化为平面PCD与平面PAB夹角的大小.
在本例中求二面角A—PB—D的大小.
3用公式cosθ=S′S,其中S′为射影面积,S为原图形面积.
[解析] ∵∠SAB=∠SAC=90°,
∴SA⊥面ABC.
∴AC为SC在底面ABC上的射影.
又∠ACB=90°,
∴SC⊥BC.
∴∠SCA为二面角S—BC—A的平面角.
一、选择题
1.设直线l的方向向量为a,平面α的法向量为b,若a·b=0,则 ( )
A.l∥α B.l α
C.l⊥α D.l α或l∥α
[答案] D
[解析] 因为a·b=0,所以a⊥b,故选D.
2.正方形ABCD所在平面外一点P,PA⊥平面ABCD,若PA=AB,则平面PAB与平面PCD所成的角的度数为( )
A.30° B.45°
C.60° D.90°
[答案] B
[解析] ∠DPA为二面角平面角,而在Rt△PAD内,∠APD=45°.故选B.
3.如图正方体ABCD-A1B1C1D1中,E、F分别是BB1和DD1的中点,则平面ECF与平面ABCD的夹角的余弦值为( )
[答案] B
二、填空题
4.正方体AC1中平面ABCD与平面A1BCD1的夹角为________.
[答案] 45°
[解析] ∠A1BA为平面角.
5 正三角形ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A—DC—B(如图②).在图②中求平面ABD与平面EFD所成二面角.
[辨析] 求二面角大小,一要注意准确计算,二要注意观察二面角是锐角还是钝角,以确定求出来的余弦值是正还是负.
