2018年高中数学第一章常用逻辑用语1.3.2命题的四种形式课件5新人教B版选修2_1(24张)
文档属性
| 名称 | 2018年高中数学第一章常用逻辑用语1.3.2命题的四种形式课件5新人教B版选修2_1(24张) |  | |
| 格式 | zip | ||
| 文件大小 | 426.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-26 17:04:04 | ||
图片预览








文档简介
课件24张PPT。命题的四种形式
1.四种命题的概念
把命题“如果p,则q”看作原命题,则它的
①逆命题是“ ”;
②否命题是“ ”;
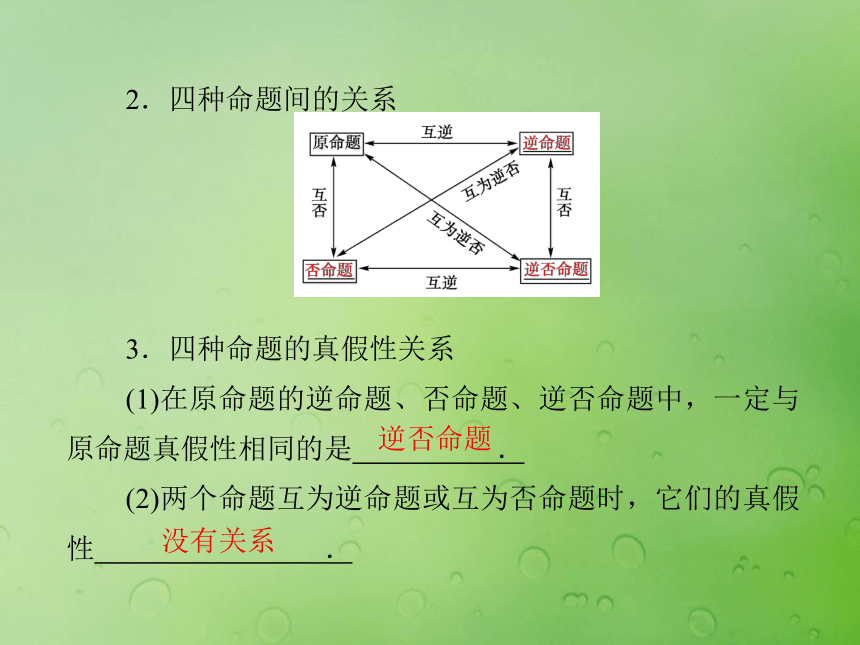
③逆否命题是“ ”.如果q,则p如果非p,则非q如果非q,则非p2.四种命题间的关系
3.四种命题的真假性关系
(1)在原命题的逆命题、否命题、逆否命题中,一定与原命题真假性相同的是 .
(2)两个命题互为逆命题或互为否命题时,它们的真假性 .逆否命题没有关系
[例1] 若a、b、c∈R,写出命题“若ac<0,则ax2+bx+c=0有两个不相等的实数根”的逆命题、否命题、逆否命题,并判断这三个命题的真假.
[分析] 认清命题的条件p和结论q,然后按定义书写逆命题、否命题、逆否命题,最后判断真假.[解析] 逆命题:“若ax2+bx+c=0(a、b、c∈R)有两个不相等的实数根,则ac<0.”它是假命题,如当a=1,b=-3,c=2时,方程x2-3x+2=0有两个不等实根x1=1,x2=2,但ac=2>0.
否命题:“若ac≥0,则方程ax2+bx+c=0(a、b、c∈R)没有两个不相等的实数根”,它是假命题,这是因为它和逆命题互为逆否命题,而逆命题是假命题的缘故.
逆否命题:“若ax2+bx+c=0(a、b、c∈R)没有两个不相等的实数根,则ac≥0.”它是真命题,因为原命题是真命题,它与原命题等价.
命题:已知a、b为实数,若x2+ax+b≤0有非空解集,则a2-4b≥0,写出该命题的逆命题、否命题、逆否命题,并判断这些命题的真假.[解析] 逆命题:已知a、b为实数,若a2-4b≥0,则x2+ax+b≤0有非空解集.
否命题:已知a、b为实数,若x2+ax+b≤0没有非空解集,则a2-4b<0.
逆否命题:已知a、b为实数,若a2-4b<0,则x2+ax+b≤0没有非空解集.
原命题、逆命题、否命题、逆否命题均为真命题.
[例2] 写出下列各命题的否定形式及命题的否命题,并分别判断它们的真假:
(1)面积相等的三角形是全等三角形;
(2)所有的方程不都是不等式;
(3)自然数的平方是正数.[解析] 原命题的否定形式:
(1)面积相等的三角形不一定是全等三角形.为真命题.
(2)所有的方程都是不等式,为假命题.
(3)自然数的平方不都是正数,为真命题.
原命题的否命题:
(1)面积不相等的三角形不是全等三角形,为真命题.
(2)有些方程是不等式,为假命题.
(3)有些自然数的平方不是正数,为真命题.[说明] 命题的否定形式与否命题是两个不同的概念,要注意区别,不能混淆.
写出下列命题的否命题及命题的否定形式,并判断真假.
(1)若m>0,则关于x的方程x2+x-m=0有实根;
(2)若x,y都是奇数,则x+y是奇数;
(3)若abc=0,则a、b、c中至少有一个为0.
[解析] (1)否命题:若m≤0,则关于x的方程x2+x-m=0无实根,假命题.
命题的否定:若m>0,则关于x的方程x2+x-m=0无实根,假命题.
(2)否命题:若x,y不都是奇数,则x+y不是奇数,假命题.
命题的否定:若x,y都是奇数,则x+y不是奇数,真命题.
(3)否命题:若abc≠0,则a、b、c全不为零,真命题.
命题的否定:若abc=0,则a、b、c全不为零,假命题.
[例3] 判断命题“已知a,x为实数,若关于x的不等式x2+(2a+1)x+a2+2≤0的解集非空,则a≥1”的逆否命题的真假.
[分析] 可以先写出逆否命题,直接判断其真假,也可以利用原命题与逆否命题的等价关系去判断原命题的真假.问题中涉及不等式的解集,还可以利用集合的包含、相等关系求解.[解析] 解法一:逆否命题为已知a,x为实数,若a<1,则关于x的不等式x2+(2a+1)x+a2+2≤0的解集为空集.
抛物线y=x2+(2a+1)x+a2+2开口向上,
对应方程的Δ=(2a+1)2-4(a2+2)=4a-7.
因为a<1,所以4a-7<0.即抛物线与x轴无交点,
所以关于x的不等式x2+(2a+1)x+a2+2≤0的解集为空集.
故逆否命题为真.[例] 设原命题为“已知A={x|-3由A∩B≠?知a>-3.∴否命题为假,从而逆命题也为假;
[辨析] 判断命题真假,应注意原命题与其逆否命题等价,否命题与逆命题等价,这为我们解决此类问题提供了新的方法,但应注意要正确写出其余命题是判断正误的前提.[正解] 逆命题“已知A={x|-3B={x|x否命题“已知A={x|-2若A∩B=?,则a≤-3,或a≥5”;
逆否命题“已知A={x|-3若a≤-3或a≥5则A∩B=?”.
先判断原命题真假,由A∩B≠?,得a>-3,因此原命题为假.从而逆否命题为假;
再判断逆命题的真假.由上知,A∩B≠?时,a>-3,由{a|-3-3},因此“-31.给出命题:“已知a,b,c,d是实数,若a≠b,且c≠d,则a+c≠b+d”,对原命题、逆命题、否命题、逆否命题而言,其中的真命题有 ( )
A.0个 B.1个 C.2个 D.4个
[答案] A
[解析] 原命题是假命题,如:3≠5,4≠2但3+4=5+2,逆命题为:“a+c≠b+d”则a≠b且c≠d也是假命题;如:3+4≠3+5中,a=b=3,c=4≠d=5,
由原命题与其逆否命题等价,知否命题和逆命题均为假命题,故选A.2.命题“若f(x)是奇函数,则f(-x)是奇函数”的否命题是
( )
A.若f(x)是偶函数,则f(-x)是偶函数
B.若f(x)不是奇函数,则f(-x)不是奇函数
C.若f(-x)是奇函数,则f(x)是奇函数
D.若f(-x)不是奇函数,则f(x)不是奇函数
[答案] B
[解析] 否命题同时否定条件和结论.3.与命题“能被6整除的整数,一定能被3整除”等价的命题是
( )
A.能被3整除的整数,一定能被6整除
B.不能被3整除的整数,一定不能被6整除
C.不能被6整除的整数,一定不能被3整除
D.不能被6整除的整数,不一定能被3整除
[答案] B
[解析] 一个命题与它的逆否命题是等价命题,选项B中的命题恰为已知命题的逆否命题.二、填空题
4.设非A是A的否定,如果非A?B,那么A是非B的________条件.
[答案] 必要
[解析] 利用原命题和逆否命题是等价的由于非A?B的逆否命题为非B?A,即A?非B,所以A是非B的必要条件,故应填必要.三、解答题
6.写出命题“若a2>b2,则a>b”的逆命题、否命题、逆否命题,并判断四种命题的真假.
[解析] 逆命题:若a>b,则a2>b2;
否命题:若a2≤b2,则a≤b;
逆否命题:若a≤b,则a2≤b2.
因为(-1)2>02,但-1<0,所以原命题不正确.
又因为-2>-3,但(-2)2<(-3)2,所以逆命题不正确.
由四种命题的关系知,四个命题都是假命题.
把命题“如果p,则q”看作原命题,则它的
①逆命题是“ ”;
②否命题是“ ”;
③逆否命题是“ ”.如果q,则p如果非p,则非q如果非q,则非p2.四种命题间的关系
3.四种命题的真假性关系
(1)在原命题的逆命题、否命题、逆否命题中,一定与原命题真假性相同的是 .
(2)两个命题互为逆命题或互为否命题时,它们的真假性 .逆否命题没有关系
[例1] 若a、b、c∈R,写出命题“若ac<0,则ax2+bx+c=0有两个不相等的实数根”的逆命题、否命题、逆否命题,并判断这三个命题的真假.
[分析] 认清命题的条件p和结论q,然后按定义书写逆命题、否命题、逆否命题,最后判断真假.[解析] 逆命题:“若ax2+bx+c=0(a、b、c∈R)有两个不相等的实数根,则ac<0.”它是假命题,如当a=1,b=-3,c=2时,方程x2-3x+2=0有两个不等实根x1=1,x2=2,但ac=2>0.
否命题:“若ac≥0,则方程ax2+bx+c=0(a、b、c∈R)没有两个不相等的实数根”,它是假命题,这是因为它和逆命题互为逆否命题,而逆命题是假命题的缘故.
逆否命题:“若ax2+bx+c=0(a、b、c∈R)没有两个不相等的实数根,则ac≥0.”它是真命题,因为原命题是真命题,它与原命题等价.
命题:已知a、b为实数,若x2+ax+b≤0有非空解集,则a2-4b≥0,写出该命题的逆命题、否命题、逆否命题,并判断这些命题的真假.[解析] 逆命题:已知a、b为实数,若a2-4b≥0,则x2+ax+b≤0有非空解集.
否命题:已知a、b为实数,若x2+ax+b≤0没有非空解集,则a2-4b<0.
逆否命题:已知a、b为实数,若a2-4b<0,则x2+ax+b≤0没有非空解集.
原命题、逆命题、否命题、逆否命题均为真命题.
[例2] 写出下列各命题的否定形式及命题的否命题,并分别判断它们的真假:
(1)面积相等的三角形是全等三角形;
(2)所有的方程不都是不等式;
(3)自然数的平方是正数.[解析] 原命题的否定形式:
(1)面积相等的三角形不一定是全等三角形.为真命题.
(2)所有的方程都是不等式,为假命题.
(3)自然数的平方不都是正数,为真命题.
原命题的否命题:
(1)面积不相等的三角形不是全等三角形,为真命题.
(2)有些方程是不等式,为假命题.
(3)有些自然数的平方不是正数,为真命题.[说明] 命题的否定形式与否命题是两个不同的概念,要注意区别,不能混淆.
写出下列命题的否命题及命题的否定形式,并判断真假.
(1)若m>0,则关于x的方程x2+x-m=0有实根;
(2)若x,y都是奇数,则x+y是奇数;
(3)若abc=0,则a、b、c中至少有一个为0.
[解析] (1)否命题:若m≤0,则关于x的方程x2+x-m=0无实根,假命题.
命题的否定:若m>0,则关于x的方程x2+x-m=0无实根,假命题.
(2)否命题:若x,y不都是奇数,则x+y不是奇数,假命题.
命题的否定:若x,y都是奇数,则x+y不是奇数,真命题.
(3)否命题:若abc≠0,则a、b、c全不为零,真命题.
命题的否定:若abc=0,则a、b、c全不为零,假命题.
[例3] 判断命题“已知a,x为实数,若关于x的不等式x2+(2a+1)x+a2+2≤0的解集非空,则a≥1”的逆否命题的真假.
[分析] 可以先写出逆否命题,直接判断其真假,也可以利用原命题与逆否命题的等价关系去判断原命题的真假.问题中涉及不等式的解集,还可以利用集合的包含、相等关系求解.[解析] 解法一:逆否命题为已知a,x为实数,若a<1,则关于x的不等式x2+(2a+1)x+a2+2≤0的解集为空集.
抛物线y=x2+(2a+1)x+a2+2开口向上,
对应方程的Δ=(2a+1)2-4(a2+2)=4a-7.
因为a<1,所以4a-7<0.即抛物线与x轴无交点,
所以关于x的不等式x2+(2a+1)x+a2+2≤0的解集为空集.
故逆否命题为真.[例] 设原命题为“已知A={x|-3
[辨析] 判断命题真假,应注意原命题与其逆否命题等价,否命题与逆命题等价,这为我们解决此类问题提供了新的方法,但应注意要正确写出其余命题是判断正误的前提.[正解] 逆命题“已知A={x|-3
逆否命题“已知A={x|-3
先判断原命题真假,由A∩B≠?,得a>-3,因此原命题为假.从而逆否命题为假;
再判断逆命题的真假.由上知,A∩B≠?时,a>-3,由{a|-3
A.0个 B.1个 C.2个 D.4个
[答案] A
[解析] 原命题是假命题,如:3≠5,4≠2但3+4=5+2,逆命题为:“a+c≠b+d”则a≠b且c≠d也是假命题;如:3+4≠3+5中,a=b=3,c=4≠d=5,
由原命题与其逆否命题等价,知否命题和逆命题均为假命题,故选A.2.命题“若f(x)是奇函数,则f(-x)是奇函数”的否命题是
( )
A.若f(x)是偶函数,则f(-x)是偶函数
B.若f(x)不是奇函数,则f(-x)不是奇函数
C.若f(-x)是奇函数,则f(x)是奇函数
D.若f(-x)不是奇函数,则f(x)不是奇函数
[答案] B
[解析] 否命题同时否定条件和结论.3.与命题“能被6整除的整数,一定能被3整除”等价的命题是
( )
A.能被3整除的整数,一定能被6整除
B.不能被3整除的整数,一定不能被6整除
C.不能被6整除的整数,一定不能被3整除
D.不能被6整除的整数,不一定能被3整除
[答案] B
[解析] 一个命题与它的逆否命题是等价命题,选项B中的命题恰为已知命题的逆否命题.二、填空题
4.设非A是A的否定,如果非A?B,那么A是非B的________条件.
[答案] 必要
[解析] 利用原命题和逆否命题是等价的由于非A?B的逆否命题为非B?A,即A?非B,所以A是非B的必要条件,故应填必要.三、解答题
6.写出命题“若a2>b2,则a>b”的逆命题、否命题、逆否命题,并判断四种命题的真假.
[解析] 逆命题:若a>b,则a2>b2;
否命题:若a2≤b2,则a≤b;
逆否命题:若a≤b,则a2≤b2.
因为(-1)2>02,但-1<0,所以原命题不正确.
又因为-2>-3,但(-2)2<(-3)2,所以逆命题不正确.
由四种命题的关系知,四个命题都是假命题.
