2018-2019学年度第一学期沪科版九年级数学上册第21章二次函数与反比例函数单元检测试题含答案
文档属性
| 名称 | 2018-2019学年度第一学期沪科版九年级数学上册第21章二次函数与反比例函数单元检测试题含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 130.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-27 00:00:00 | ||
图片预览




文档简介
2018-2019学年度第一学期沪科版九年级数上册_
第21章_ 二次函数与反比例函数_单元检测试题_
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.下面的函数是二次函数的是( )
A. B.
C. D.
?2.点在反比例函数的图象上,则的值是( )
A. B. C. D.
?3.长方形的周长为,其中一边为(其中),面积为,则这样的长方形中与的关系可以写为( )
A. B.
C. D.
?4.正比例函数与反比例函数的图象相交于、两点,过点作轴的垂线交轴于点,连结,若的面积为,则( )
A. B. C. D.
?5.购买斤水果需元,购买一斤水果的单价与的关系式是( )
A. B.(为自然数
C.(为整数) D.(为正整数)
?6.甲、乙两地相距,汽车从甲地开往乙地,速度和所需时间之间的函数关系图象大致是( )
A. B.
C. D.
?7.定义:给定关于的函数,对于该函数图象上任意两点,,当时,都有为增函数.根据以上定义,可以判断下面所给的函数中:①;②;③;④.是增函数的有( )
A.①② B.①③ C.①④ D.③④
?8.设矩形的长、宽分别为、,面积为,则关于的函数图象大致是( )
A. B.
C. D.
?9.若关于的二次函数的图象与轴仅有一个公共点,则的取值范围是( )
A. B.
C. D.且
?10.如图,已知的顶点和边的中点都在双曲线的一个分支上,点在轴上,于,则的面积为( )
A. B. C. D.
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.已知函数是二次函数,则________.
?12.抛物线的对称轴是直线________.
?13.如图,已知二次函数与一次函数的图象相交于、两点,则关于的不等式的解集是________.
?14.设、、三点依次分别是抛物线与轴的交点以及与轴的两个交点,则的面积是________.
?15.对于函数,使得随的增大而增大的的取值范围是________.
?16.某商品的进价为每件元,售价为每件元,每个月可卖出件;如果每件商品的售价上涨元,则每个月少卖件(每件售价不能高于元).设每件商品的售价上涨元(为正整数)月销售利润为元,当________元时,最大利润________元.
?
17.若二次函数的图象的对称轴是经过点且平行于轴的直线,则关于的方程的解为________.
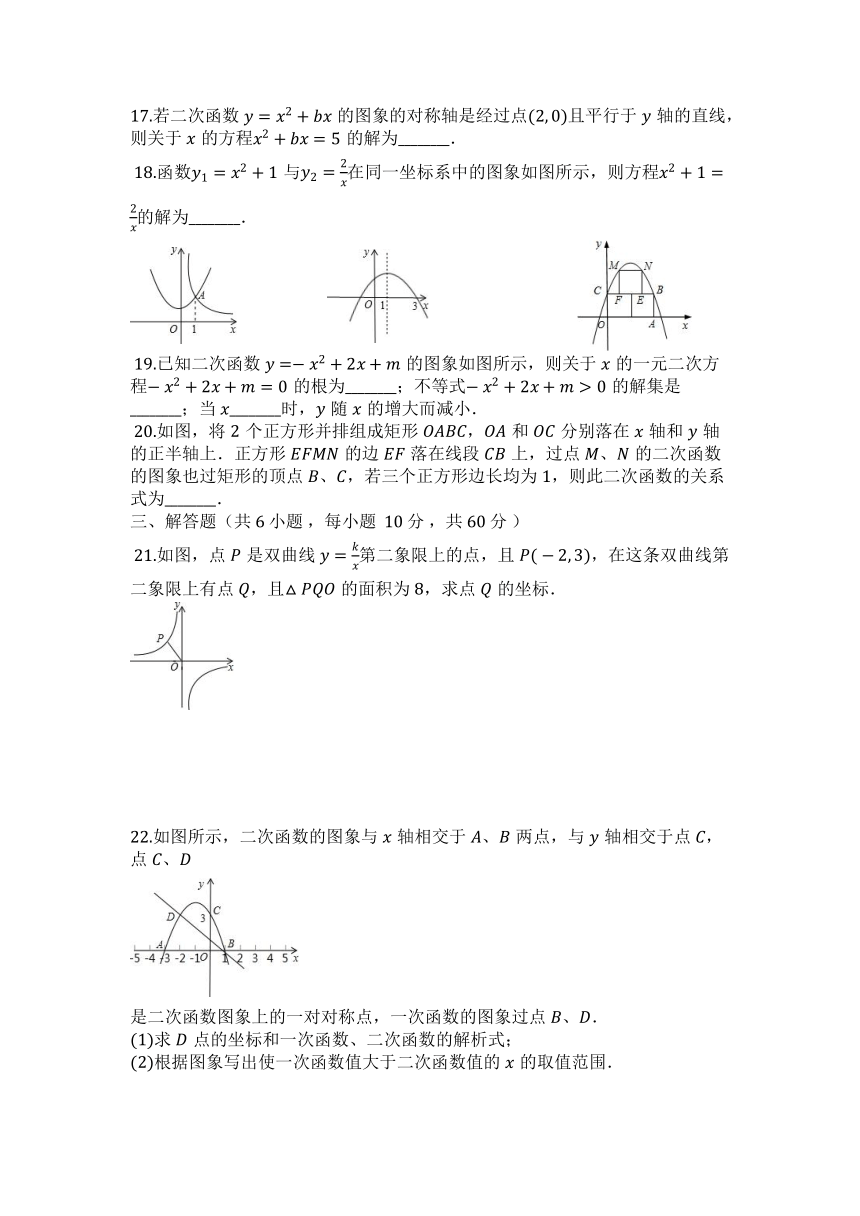
?18.函数与在同一坐标系中的图象如图所示,则方程的解为________.
?19.已知二次函数的图象如图所示,则关于的一元二次方程的根为________;不等式的解集是________;当________时,随的增大而减小.
?20.如图,将个正方形并排组成矩形,和分别落在轴和轴的正半轴上.正方形的边落在线段上,过点、的二次函数的图象也过矩形的顶点、,若三个正方形边长均为,则此二次函数的关系式为________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.如图,点是双曲线第二象限上的点,且,在这条双曲线第二象限上有点,且的面积为,求点的坐标.
?
22.如图所示,二次函数的图象与轴相交于、两点,与轴相交于点,点、
是二次函数图象上的一对对称点,一次函数的图象过点、.
求点的坐标和一次函数、二次函数的解析式;
根据图象写出使一次函数值大于二次函数值的的取值范围.
?
23.某种家用电器,其进价是元/个.经过市场销售后发现:在一周内,当售价是元/个时,可售出个,且售价每降低元,就可多售出个.若供货商规定这种家用电器售价不能低于元/个,代理销售商每周要完成不低于个的销售任务.
试确定周销售量(个)与售价(元/个)之间的函数关系式,并求出自变量的取值范围;
当售价(元/个)定为多少时,商场每周销售这种家用电器所获得的利润(元)最大?最大利润是
多少?
?
24.、分别为反比例函数和反比例函数上的点,.
求的值;
若轴,求的长;
设与轴交于点,当时,求点坐标.
?
25.如图,小明的父亲在相距米的两棵树间拴了一根绳子,给他做了简易的秋千,拴绳子的地方距地面高都是米,绳子自然下垂呈抛物线状,身高米的小明距较近的那棵树米时,头部刚好接触到绳子.
以水平的地面为轴,两棵树间距离的中点为原点,建立如图所示的平面直角坐标系,求出抛物线的解析式;
求绳子的最低点离地面的距离.
?
26.已知:中,,两条直角边,.如图,在轴上,点在反比例函数第一象限的分支上,与轴交于点,记四边形面积为;如图点在反比例函数第一象限的分支上,在轴上,与轴交于点,记四边形面积为.试比较与的大小,并说明理由.
答案
1.B
2.B
3.C
4.A
5.A
6.C
7.B
8.B
9.B
10.B
11.
12.
13.或
14.
15.
16.或
17.,
18.
19.或
20.
21.解:作轴于,轴于,如图,
把代入得,
所以反比例函数解析式为,
∵,
∴,
设的坐标为,
∴,
当,解得(舍去),,
当,解得,(舍去),
∴点坐标为或.
22.解:∵,,,
∴设二次函数的解析式为:,
将点代入函数解析式得:,
∴,
∴此二次函数的解析式为:,
∴此二次函数的对称轴为:,
∵点、是二次函数图象上的一对对称点,
∴,
∴设直线的解析式为:,
∴,
解得:,
∴此一次函数的解析式为:;根据图象得:
一次函数值大于二次函数值的的取值范围为:或.
23.解:,
即,
由题意得:且.
解得:;
,
所以当时,有最大值为元.
24.解:作轴于,轴于,如图,
设,,
∵,
∴,即,
而,
∴,
∴,
∴,即,
∴,
∴,
∴,
在中,;如图,∵轴,
∴,
而,,
∴,解得,
∵,
∴,
∴;作轴于,轴于,如图,
∵,
∴,
∴,即,
∴,
而,
∴,解得,
∴.
25.解:设抛物线的解析式为.
由题意知抛物线过点、
将上述两点的坐标代入得:,解得
∴绳子所在抛物线的解析式为.当时,.
∴绳子的最低点离地面的距离为米.
26.解:解法一:∵轴,,在上,
∴,
∴,
∴,
∴,
∴.
∵
∴,
∴.
同理:,,
∴,
∴
∴,
∴
∴;
解法二:∵,点在上,
∴,,
∴,
∴.
设直线,则
,
解得∴,即,
∴,
∴.
同理可得:如图中,,,设直线,则
,
解得,即,
∴,
∴.
∴.
第21章_ 二次函数与反比例函数_单元检测试题_
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.下面的函数是二次函数的是( )
A. B.
C. D.
?2.点在反比例函数的图象上,则的值是( )
A. B. C. D.
?3.长方形的周长为,其中一边为(其中),面积为,则这样的长方形中与的关系可以写为( )
A. B.
C. D.
?4.正比例函数与反比例函数的图象相交于、两点,过点作轴的垂线交轴于点,连结,若的面积为,则( )
A. B. C. D.
?5.购买斤水果需元,购买一斤水果的单价与的关系式是( )
A. B.(为自然数
C.(为整数) D.(为正整数)
?6.甲、乙两地相距,汽车从甲地开往乙地,速度和所需时间之间的函数关系图象大致是( )
A. B.
C. D.
?7.定义:给定关于的函数,对于该函数图象上任意两点,,当时,都有为增函数.根据以上定义,可以判断下面所给的函数中:①;②;③;④.是增函数的有( )
A.①② B.①③ C.①④ D.③④
?8.设矩形的长、宽分别为、,面积为,则关于的函数图象大致是( )
A. B.
C. D.
?9.若关于的二次函数的图象与轴仅有一个公共点,则的取值范围是( )
A. B.
C. D.且
?10.如图,已知的顶点和边的中点都在双曲线的一个分支上,点在轴上,于,则的面积为( )
A. B. C. D.
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.已知函数是二次函数,则________.
?12.抛物线的对称轴是直线________.
?13.如图,已知二次函数与一次函数的图象相交于、两点,则关于的不等式的解集是________.
?14.设、、三点依次分别是抛物线与轴的交点以及与轴的两个交点,则的面积是________.
?15.对于函数,使得随的增大而增大的的取值范围是________.
?16.某商品的进价为每件元,售价为每件元,每个月可卖出件;如果每件商品的售价上涨元,则每个月少卖件(每件售价不能高于元).设每件商品的售价上涨元(为正整数)月销售利润为元,当________元时,最大利润________元.
?
17.若二次函数的图象的对称轴是经过点且平行于轴的直线,则关于的方程的解为________.
?18.函数与在同一坐标系中的图象如图所示,则方程的解为________.
?19.已知二次函数的图象如图所示,则关于的一元二次方程的根为________;不等式的解集是________;当________时,随的增大而减小.
?20.如图,将个正方形并排组成矩形,和分别落在轴和轴的正半轴上.正方形的边落在线段上,过点、的二次函数的图象也过矩形的顶点、,若三个正方形边长均为,则此二次函数的关系式为________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.如图,点是双曲线第二象限上的点,且,在这条双曲线第二象限上有点,且的面积为,求点的坐标.
?
22.如图所示,二次函数的图象与轴相交于、两点,与轴相交于点,点、
是二次函数图象上的一对对称点,一次函数的图象过点、.
求点的坐标和一次函数、二次函数的解析式;
根据图象写出使一次函数值大于二次函数值的的取值范围.
?
23.某种家用电器,其进价是元/个.经过市场销售后发现:在一周内,当售价是元/个时,可售出个,且售价每降低元,就可多售出个.若供货商规定这种家用电器售价不能低于元/个,代理销售商每周要完成不低于个的销售任务.
试确定周销售量(个)与售价(元/个)之间的函数关系式,并求出自变量的取值范围;
当售价(元/个)定为多少时,商场每周销售这种家用电器所获得的利润(元)最大?最大利润是
多少?
?
24.、分别为反比例函数和反比例函数上的点,.
求的值;
若轴,求的长;
设与轴交于点,当时,求点坐标.
?
25.如图,小明的父亲在相距米的两棵树间拴了一根绳子,给他做了简易的秋千,拴绳子的地方距地面高都是米,绳子自然下垂呈抛物线状,身高米的小明距较近的那棵树米时,头部刚好接触到绳子.
以水平的地面为轴,两棵树间距离的中点为原点,建立如图所示的平面直角坐标系,求出抛物线的解析式;
求绳子的最低点离地面的距离.
?
26.已知:中,,两条直角边,.如图,在轴上,点在反比例函数第一象限的分支上,与轴交于点,记四边形面积为;如图点在反比例函数第一象限的分支上,在轴上,与轴交于点,记四边形面积为.试比较与的大小,并说明理由.
答案
1.B
2.B
3.C
4.A
5.A
6.C
7.B
8.B
9.B
10.B
11.
12.
13.或
14.
15.
16.或
17.,
18.
19.或
20.
21.解:作轴于,轴于,如图,
把代入得,
所以反比例函数解析式为,
∵,
∴,
设的坐标为,
∴,
当,解得(舍去),,
当,解得,(舍去),
∴点坐标为或.
22.解:∵,,,
∴设二次函数的解析式为:,
将点代入函数解析式得:,
∴,
∴此二次函数的解析式为:,
∴此二次函数的对称轴为:,
∵点、是二次函数图象上的一对对称点,
∴,
∴设直线的解析式为:,
∴,
解得:,
∴此一次函数的解析式为:;根据图象得:
一次函数值大于二次函数值的的取值范围为:或.
23.解:,
即,
由题意得:且.
解得:;
,
所以当时,有最大值为元.
24.解:作轴于,轴于,如图,
设,,
∵,
∴,即,
而,
∴,
∴,
∴,即,
∴,
∴,
∴,
在中,;如图,∵轴,
∴,
而,,
∴,解得,
∵,
∴,
∴;作轴于,轴于,如图,
∵,
∴,
∴,即,
∴,
而,
∴,解得,
∴.
25.解:设抛物线的解析式为.
由题意知抛物线过点、
将上述两点的坐标代入得:,解得
∴绳子所在抛物线的解析式为.当时,.
∴绳子的最低点离地面的距离为米.
26.解:解法一:∵轴,,在上,
∴,
∴,
∴,
∴,
∴.
∵
∴,
∴.
同理:,,
∴,
∴
∴,
∴
∴;
解法二:∵,点在上,
∴,,
∴,
∴.
设直线,则
,
解得∴,即,
∴,
∴.
同理可得:如图中,,,设直线,则
,
解得,即,
∴,
∴.
∴.
