2018-2019学年度第一学期沪科版九年级数学上册第22章相似形单元检测试题含答案
文档属性
| 名称 | 2018-2019学年度第一学期沪科版九年级数学上册第22章相似形单元检测试题含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 159.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-27 06:25:12 | ||
图片预览


文档简介
2018-2019学年度第一学期沪科版九年级数上册_
第22章_相似形 _单元检测试题_
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.已知,则的值是( )
A. B. C. D.
?2.某市地图上有一块草地,三边长分别为、、,已知这块草地最短边的实际长度为,则这块草地的实际面积是( )
A. B. C. D.
?3.如图,在中,是边上的中线,点在边上,且,交与点,则的比为( )
A. B. C. D.
?4.在中,,是的高,是的中点,、的延长线相交于点,则图中相似三角形有( )
A.对 B.对 C.对 D.对
?5.用幻灯机将一个三角形的面积放大为原来的倍,下列说法中正确的是( )
A.放大后、、是原来的倍 B.放大后周长是原来的倍
C.放大后对应边长是原来的倍 D.放大后对应中线长是原来的倍
?6.如图,在中,点、分、边上,,若,,则等于( )
A. B. C. D.
?7.在中,,,,,最短边是,则它的最长边的长度为( )
A. B.
C. D.
?
8.如图,已知点是边的中点,,,,则等于( )
A. B. C. D.
?9.如图,在内画有边长为,,的三个正方形,则的值为( )
A. B. C. D.
?10.如图所示,在正方形中,是的中点,是上的一点,,下列结论:①;②;③;④.其中正确的有( )
A.个 B.个 C.个 D.个
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.如图,要使,还需增添的条件是________(写一个即可).
?12.润扬长江大桥是我国第一座由悬索桥和斜拉桥构成的组合型特大桥梁,其北汊桥为斜拉桥,它是利用一组组钢索,把桥面重力传递到两侧的高塔上.如图,、、、是斜拉桥上条互相平行的钢索,并且,,如果钢索米,钢索米,那么钢索的长为________米.
?13.如图,与相交于点,,,.当________时,图中的两个三角形相似.(只需写出一个条件即可)
?14.如图,在中,,,平分交于点,下列结论中:
①;②;③;④若,则,
其中正确结论的个数是________个.
?15.在平面直角坐标系中,顶点的坐标为,若以原点为位似中心,画的位似图形,使与的相似比等于,则点的坐标为________.
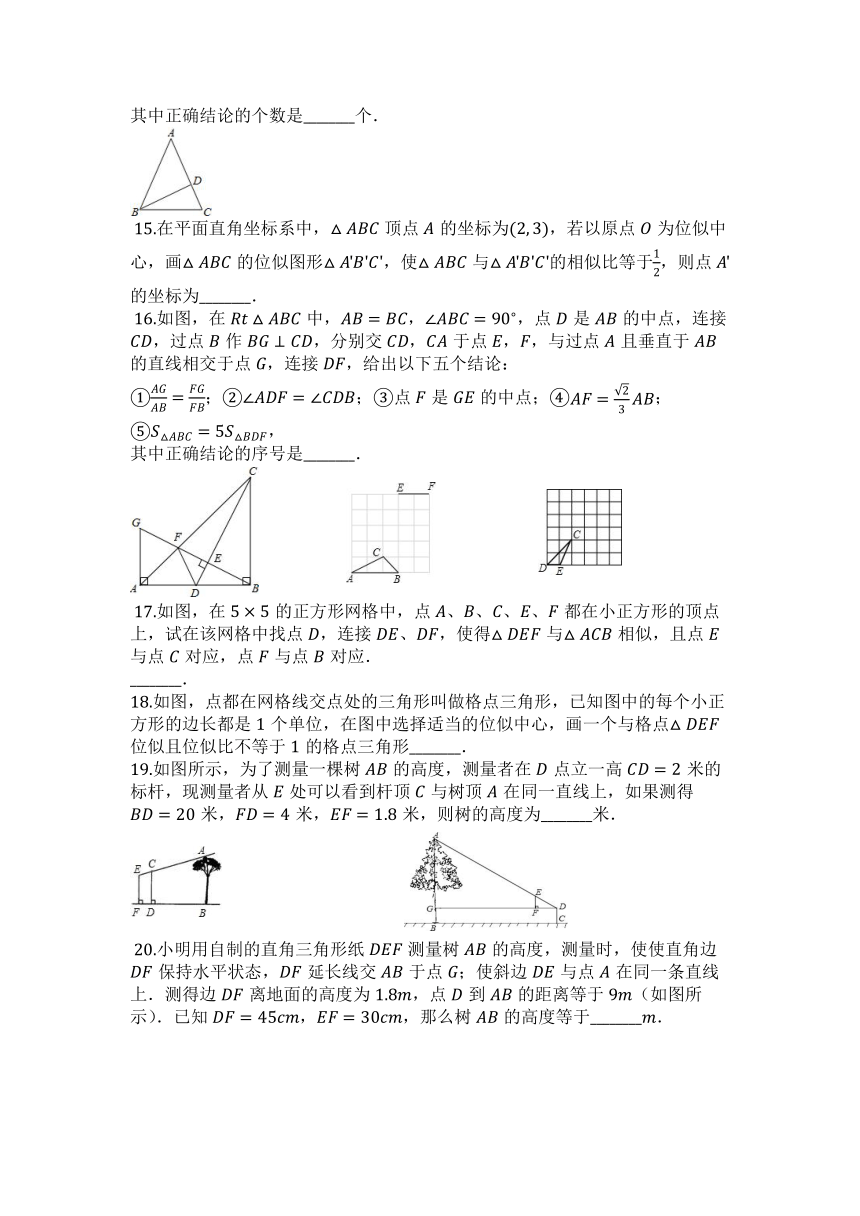
?16.如图,在中,,,点是的中点,连接,过点作,分别交,于点,,与过点且垂直于的直线相交于点,连接,给出以下五个结论:
①;②;③点是的中点;④;⑤,
其中正确结论的序号是________.
?17.如图,在的正方形网格中,点、、、、都在小正方形的顶点上,试在该网格中找点,连接、,使得与相似,且点与点对应,点与点对应.
________.
18.如图,点都在网格线交点处的三角形叫做格点三角形,已知图中的每个小正方形的边长都是个单位,在图中选择适当的位似中心,画一个与格点位似且位似比不等于的格点三角形________.
19.如图所示,为了测量一棵树的高度,测量者在点立一高米的标杆,现测量者从处可以看到杆顶与树顶在同一直线上,如果测得米,米,米,则树的高度为________米.
?20.小明用自制的直角三角形纸测量树的高度,测量时,使使直角边保持水平状态,延长线交于点;使斜边与点在同一条直线上.测得边离地面的高度为,点到的距离等于(如图所示).已知,,那么树的高度等于________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
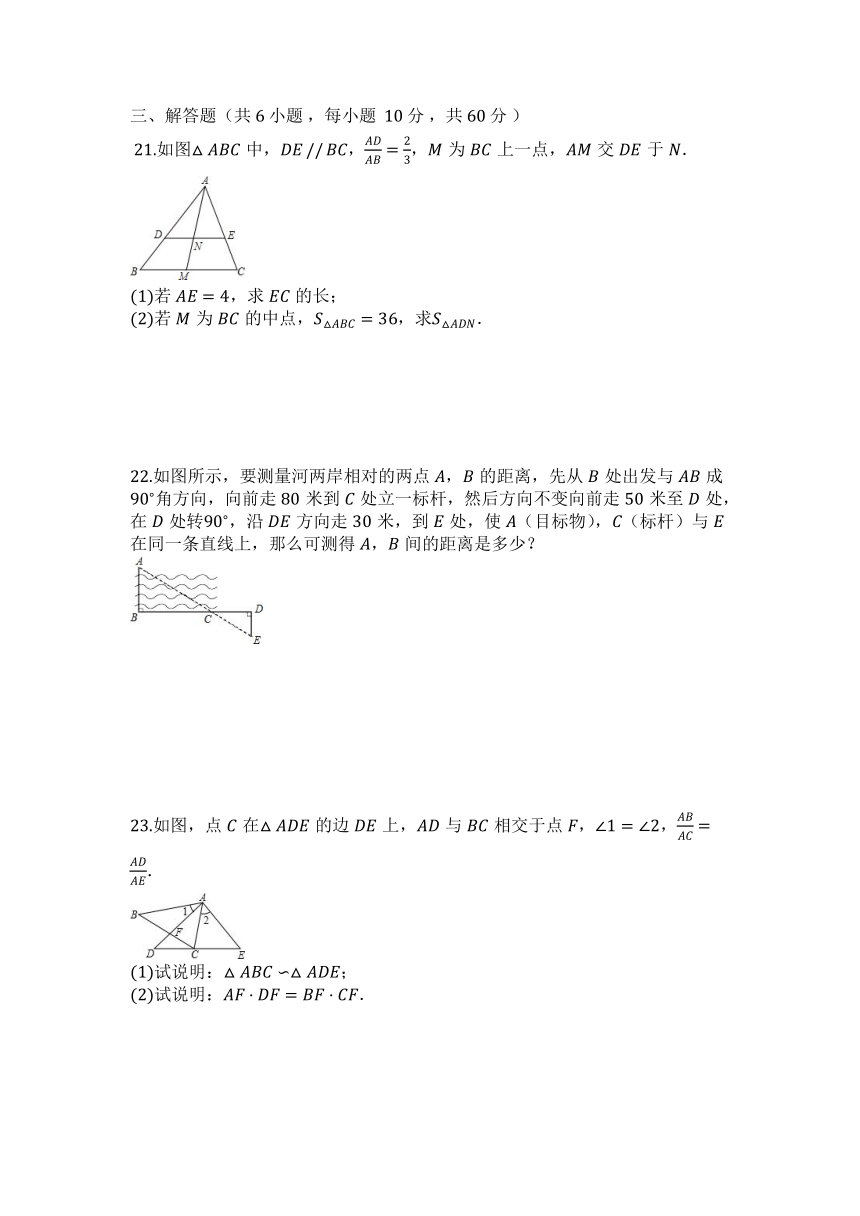
?21.如图中,,,为上一点,交于.
若,求的长;
若为的中点,,求.
?
22.如图所示,要测量河两岸相对的两点,的距离,先从处出发与成角方向,向前走米到处立一标杆,然后方向不变向前走米至处,在处转,沿方向走米,到处,使(目标物),(标杆)与在同一条直线上,那么可测得,间的距离是多少?
?
23.如图,点在的边上,与相交于点,,.
试说明:;
试说明:.
?
24.如图,在梯形中,,,且对角线,
试问:
①与相似吗?请说明理由;
②若,,请求出的长.
?
25.如图,矩形的对角线、相交于点,,.求证:四边形是菱形;25.
如图,在中,点在边上,,,.求的长.
?
26.如图,直线交轴正半轴于点,交轴正半轴于点,且、满足
求、两点的坐标;
为的中点,连接,过点作于,交于,求证:;
如图,为轴上点右侧任意一点,以为边作等腰,其中,直线交轴于点,当点在轴上运动时,线段的长是否发生变化?若不变,求其值;若变化,求线段的取值范围.
答案
1.D
2.C
3.A
4.B
5.B
6.D
7.B
8.B
9.B
10.B
11.
12.
13.
14.
15.或
16.①②④
17.
18.
19.
20.
21.解:∵,
∴,
∵,
∴,
∴;∵为的中点,
∴,
∵,
∴,
∴,
∴.
22.解:∵,,
∴,
∴,
∴,
∴,
∴米,
∴的长为米.
23.证明:∵,
∴,
∴,
∵,
∴,
∴;证明:∵,
∴,
∵,
∴,
∴,
∴.
24.解:①∵(已知),
∴(垂直性质).
而(已知),
∴(等量代换).
又∵(已知),
∴(两直线平行,内错角相等).
∴(如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似).
②∵,
∴.
而,,
∴.
25.证明:
∵,,
∴四边形是平行四边形,
∵四边形是矩形,
∴,
∴四边形是菱形;解:∵,,
∴,
∴,
∵,,
∴.
26.解:∵,
∴,.
∵,,
∴,
∴点的坐标为,点的坐标为;
过点作轴于,如图,
则有,
∴,
∴,
∴.
设,则有,.
∵,,,
∴,,
∴,
∴,
∴,
解得:.
∴,,
∴,
又∵,
∴,
∴;如图,
∵,,,,
∴,
∴、、、四点共圆,
∴,
∴,
∴,
∴.
∴当点在轴上运动时,线段的长不变,等于.
第22章_相似形 _单元检测试题_
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.已知,则的值是( )
A. B. C. D.
?2.某市地图上有一块草地,三边长分别为、、,已知这块草地最短边的实际长度为,则这块草地的实际面积是( )
A. B. C. D.
?3.如图,在中,是边上的中线,点在边上,且,交与点,则的比为( )
A. B. C. D.
?4.在中,,是的高,是的中点,、的延长线相交于点,则图中相似三角形有( )
A.对 B.对 C.对 D.对
?5.用幻灯机将一个三角形的面积放大为原来的倍,下列说法中正确的是( )
A.放大后、、是原来的倍 B.放大后周长是原来的倍
C.放大后对应边长是原来的倍 D.放大后对应中线长是原来的倍
?6.如图,在中,点、分、边上,,若,,则等于( )
A. B. C. D.
?7.在中,,,,,最短边是,则它的最长边的长度为( )
A. B.
C. D.
?
8.如图,已知点是边的中点,,,,则等于( )
A. B. C. D.
?9.如图,在内画有边长为,,的三个正方形,则的值为( )
A. B. C. D.
?10.如图所示,在正方形中,是的中点,是上的一点,,下列结论:①;②;③;④.其中正确的有( )
A.个 B.个 C.个 D.个
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.如图,要使,还需增添的条件是________(写一个即可).
?12.润扬长江大桥是我国第一座由悬索桥和斜拉桥构成的组合型特大桥梁,其北汊桥为斜拉桥,它是利用一组组钢索,把桥面重力传递到两侧的高塔上.如图,、、、是斜拉桥上条互相平行的钢索,并且,,如果钢索米,钢索米,那么钢索的长为________米.
?13.如图,与相交于点,,,.当________时,图中的两个三角形相似.(只需写出一个条件即可)
?14.如图,在中,,,平分交于点,下列结论中:
①;②;③;④若,则,
其中正确结论的个数是________个.
?15.在平面直角坐标系中,顶点的坐标为,若以原点为位似中心,画的位似图形,使与的相似比等于,则点的坐标为________.
?16.如图,在中,,,点是的中点,连接,过点作,分别交,于点,,与过点且垂直于的直线相交于点,连接,给出以下五个结论:
①;②;③点是的中点;④;⑤,
其中正确结论的序号是________.
?17.如图,在的正方形网格中,点、、、、都在小正方形的顶点上,试在该网格中找点,连接、,使得与相似,且点与点对应,点与点对应.
________.
18.如图,点都在网格线交点处的三角形叫做格点三角形,已知图中的每个小正方形的边长都是个单位,在图中选择适当的位似中心,画一个与格点位似且位似比不等于的格点三角形________.
19.如图所示,为了测量一棵树的高度,测量者在点立一高米的标杆,现测量者从处可以看到杆顶与树顶在同一直线上,如果测得米,米,米,则树的高度为________米.
?20.小明用自制的直角三角形纸测量树的高度,测量时,使使直角边保持水平状态,延长线交于点;使斜边与点在同一条直线上.测得边离地面的高度为,点到的距离等于(如图所示).已知,,那么树的高度等于________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.如图中,,,为上一点,交于.
若,求的长;
若为的中点,,求.
?
22.如图所示,要测量河两岸相对的两点,的距离,先从处出发与成角方向,向前走米到处立一标杆,然后方向不变向前走米至处,在处转,沿方向走米,到处,使(目标物),(标杆)与在同一条直线上,那么可测得,间的距离是多少?
?
23.如图,点在的边上,与相交于点,,.
试说明:;
试说明:.
?
24.如图,在梯形中,,,且对角线,
试问:
①与相似吗?请说明理由;
②若,,请求出的长.
?
25.如图,矩形的对角线、相交于点,,.求证:四边形是菱形;25.
如图,在中,点在边上,,,.求的长.
?
26.如图,直线交轴正半轴于点,交轴正半轴于点,且、满足
求、两点的坐标;
为的中点,连接,过点作于,交于,求证:;
如图,为轴上点右侧任意一点,以为边作等腰,其中,直线交轴于点,当点在轴上运动时,线段的长是否发生变化?若不变,求其值;若变化,求线段的取值范围.
答案
1.D
2.C
3.A
4.B
5.B
6.D
7.B
8.B
9.B
10.B
11.
12.
13.
14.
15.或
16.①②④
17.
18.
19.
20.
21.解:∵,
∴,
∵,
∴,
∴;∵为的中点,
∴,
∵,
∴,
∴,
∴.
22.解:∵,,
∴,
∴,
∴,
∴,
∴米,
∴的长为米.
23.证明:∵,
∴,
∴,
∵,
∴,
∴;证明:∵,
∴,
∵,
∴,
∴,
∴.
24.解:①∵(已知),
∴(垂直性质).
而(已知),
∴(等量代换).
又∵(已知),
∴(两直线平行,内错角相等).
∴(如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似).
②∵,
∴.
而,,
∴.
25.证明:
∵,,
∴四边形是平行四边形,
∵四边形是矩形,
∴,
∴四边形是菱形;解:∵,,
∴,
∴,
∵,,
∴.
26.解:∵,
∴,.
∵,,
∴,
∴点的坐标为,点的坐标为;
过点作轴于,如图,
则有,
∴,
∴,
∴.
设,则有,.
∵,,,
∴,,
∴,
∴,
∴,
解得:.
∴,,
∴,
又∵,
∴,
∴;如图,
∵,,,,
∴,
∴、、、四点共圆,
∴,
∴,
∴,
∴.
∴当点在轴上运动时,线段的长不变,等于.
