2017-2018学年度第一学期人教版九年级数学上册圆的有关性质同步检测含答案
文档属性
| 名称 | 2017-2018学年度第一学期人教版九年级数学上册圆的有关性质同步检测含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 146.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-27 07:09:54 | ||
图片预览

文档简介
2017-2018学年度第一学期人教版九年级数学上册
24.1 圆的有关性质 同步检测
考试总分:100 分 考试时间:60 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 8 小题 ,每小题 3 分 ,共 24 分 )
?1.在半径为的中,弦长为的弦所对的圆心角为( )
A. B. C. D.
?2.下列说法不正确的是( )
A.圆是轴对称图形,它有无数条对称轴
B.圆的半径、弦长的一半、弦上的弦心距能组成一直角三角形,且圆的半径是此直角三角形的斜边
C.弦长相等,则弦所对的弦心距也相等
D.垂直于弦的直径平分这条弦,并且平分弦所对的弧
?3.已知的弦长为厘米,弦的弦心距为厘米,则的直径等于( )
A.厘米 B.厘米 C.厘米 D.厘米
?4.高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以为圆心的圆的一部分,路面米,净高米,则此圆的半径
A.米 B.米 C.米 D.米
?5.如图,为的直径,弦,垂足为点,连接,若,,则的长度为( )
A. B. C. D.
?6.如图,在中,若是的中点,则图中与相等的角有( )
A.个 B.个 C.个 D.个
?7.下列命题中,是真命题的为( )
A.三个点确定一个圆
B.一个圆中可以有无数条弦,但只有一条直径
C.圆既是轴对称图形,又是中心对称图形
D.同弧所对的圆周角与圆心角相等
?
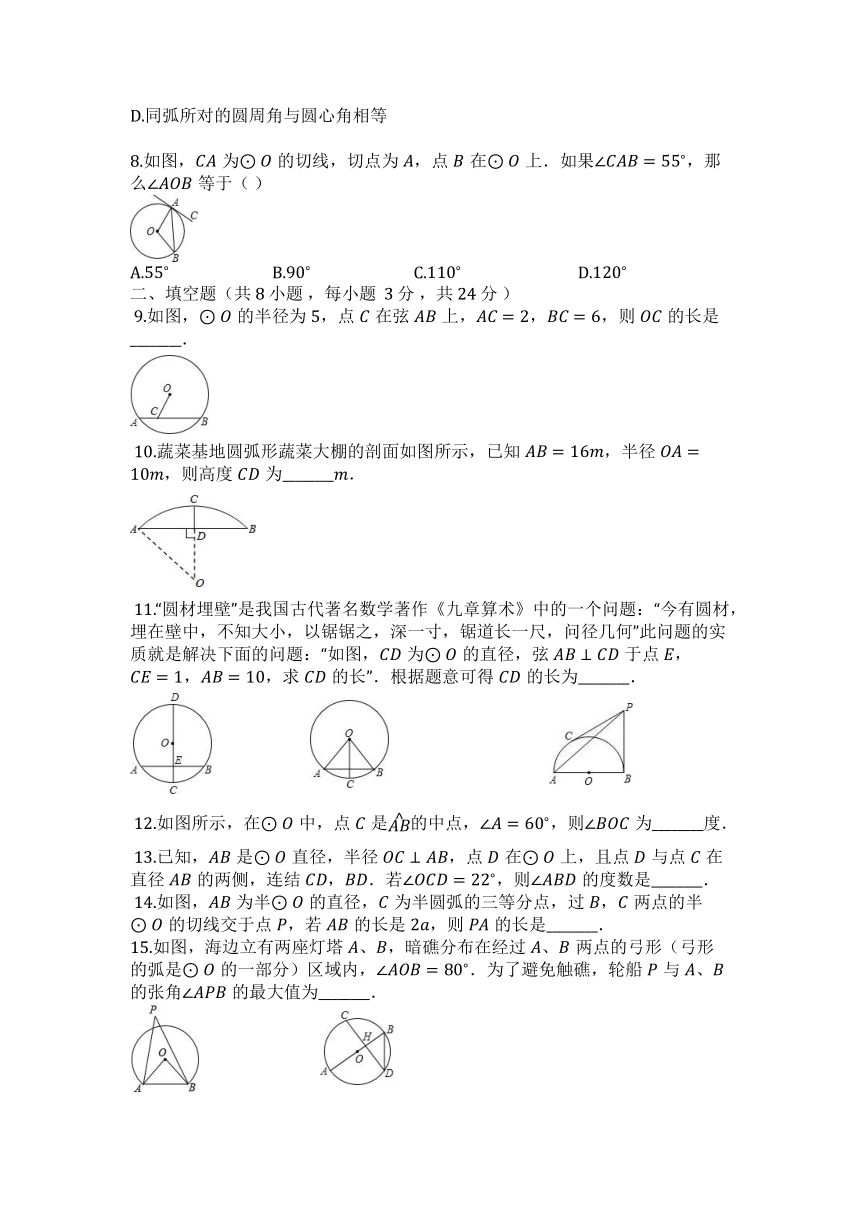
8.如图,为的切线,切点为,点在上.如果,那么等于( )
A. B. C. D.
二、填空题(共 8 小题 ,每小题 3 分 ,共 24 分 )
?9.如图,的半径为,点在弦上,,,则的长是________.
?10.蔬菜基地圆弧形蔬菜大棚的剖面如图所示,已知,半径,则高度为________.
?11.“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何”此问题的实质就是解决下面的问题:“如图,为的直径,弦于点,,,求的长”.根据题意可得的长为________.
?12.如图所示,在中,点是的中点,,则为________度.
?13.已知,是直径,半径,点在上,且点与点在直径的两侧,连结,.若,则的度数是________.
?14.如图,为半的直径,为半圆弧的三等分点,过,两点的半的切线交于点,若的长是,则的长是________.
15.如图,海边立有两座灯塔、,暗礁分布在经过、两点的弓形(弓形的弧是的一部分)区域内,.为了避免触礁,轮船与、的张角的最大值为________.
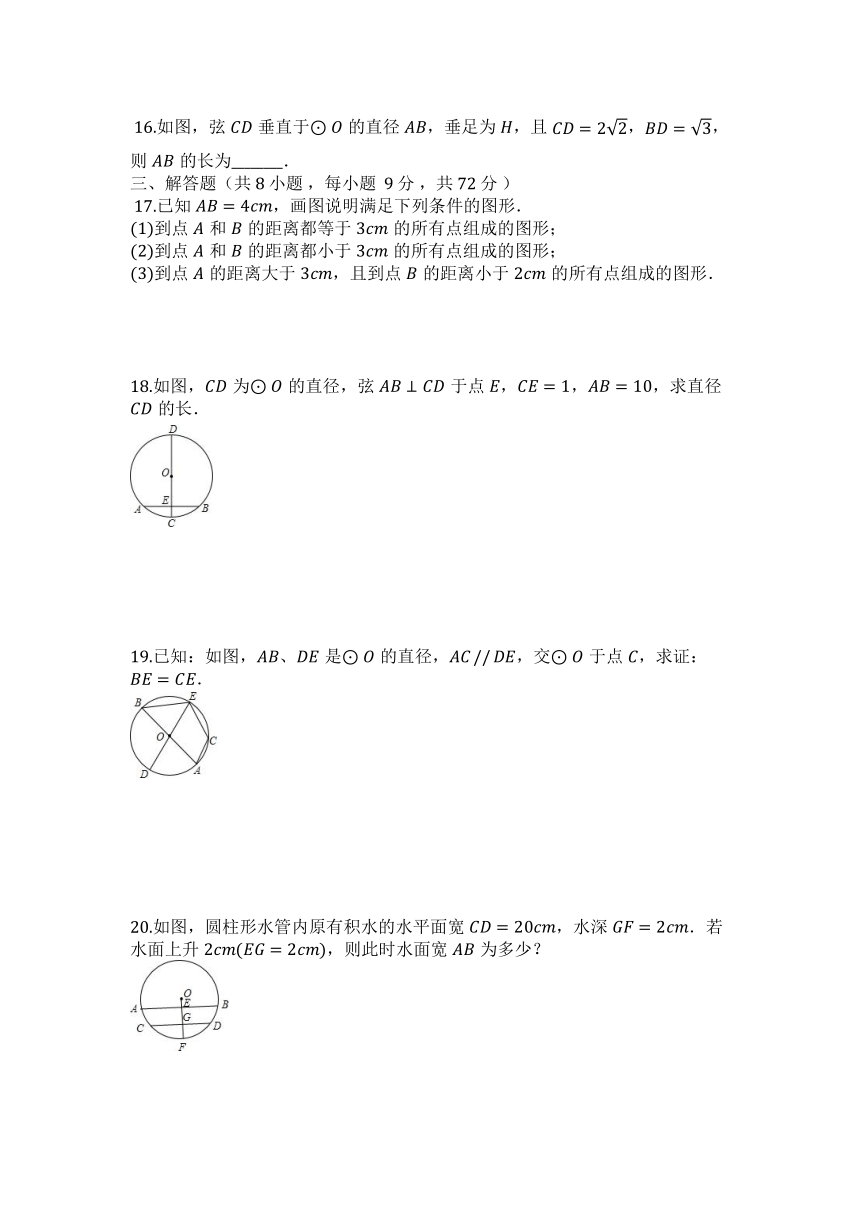
?16.如图,弦垂直于的直径,垂足为,且,,则的长为________.
三、解答题(共 8 小题 ,每小题 9 分 ,共 72 分 )
?17.已知,画图说明满足下列条件的图形.
到点和的距离都等于的所有点组成的图形;
到点和的距离都小于的所有点组成的图形;
到点的距离大于,且到点的距离小于的所有点组成的图形.
?
18.如图,为的直径,弦于点,,,求直径的长.
?
19.已知:如图,、是的直径,,交于点,求证:.
?
20.如图,圆柱形水管内原有积水的水平面宽,水深.若水面上升,则此时水面宽为多少?
?
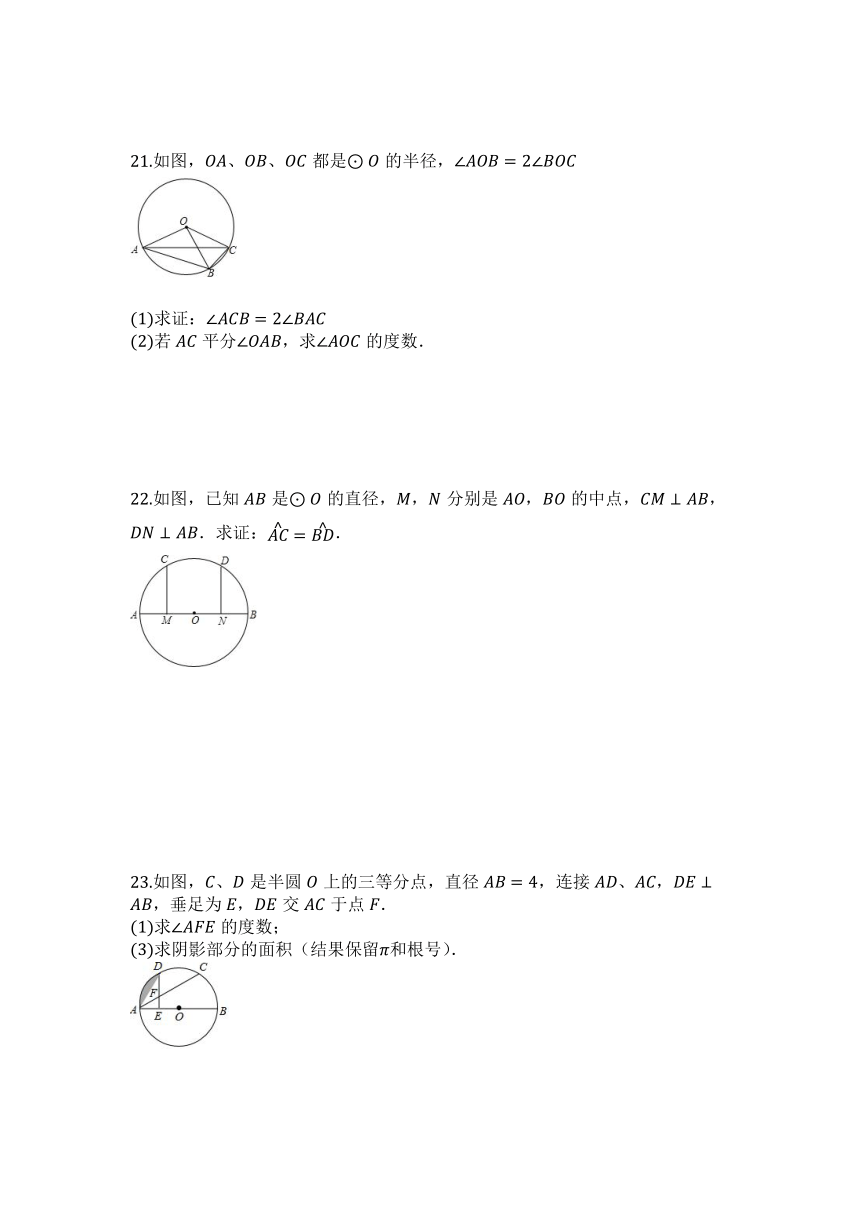
21.如图,、、都是的半径,
求证:
若平分,求的度数.
?
22.如图,已知是的直径,,分别是,的中点,,.求证:.
?
23.如图,、是半圆上的三等分点,直径,连接、,,垂足为,交于点.
求的度数;
求阴影部分的面积(结果保留和根号).
?
24.已知,如图,四边形中,,、分别是、的中点,则结论:
;
成立吗?请说明理由.
答案
1.B
2.C
3.C
4.B
5.A
6.C
7.C
8.C
9.
10.
11.
12.
13.或
14.
15.
16.
17.解:如图,分别以点和点为圆心,为半径画与,两圆的交点、为所求;
如图,分别以点和点为圆心,为半径画与,两圆的重叠部分为所求;如图,以点为圆心,为半径画,以点为圆心,为半径画,则中除去两圆的重叠部分为所求.
18.解:∵是的直径,
∴
∵
∴
设
∴
根据勾股定理:
解得
∴
19.证明:连接,
∵,
∴,,
∵,
∴,
∴.
20.解:如图所示,连接、.
设的半径是,则,.
∵,
∴.
在直角三角形中,根据勾股定理,得
,
解,得.
在直角三角形中,根据勾股定理,得
.
根据垂径定理,得.
21.证明:在中,
∵,,
∵.
∴.解:设.
∵平分,
∴,
∵,,
∴,
在中,
,
∴,
解得:,
∴.
22.证明:连结、,如图,
∵是的直径,,分别是,的中点,
∴,
∵,,
∴,
在和中,
,
∴,
∴,
∴.
23.解:连接,,
∵、是半圆上的三等分点,
∴,
∴,
∴,
∵,
∴,
∴;
由知,,
∵,,
∴是等边三角形,,
∵,
∴,
∴.
24.解:均成立.理由如下:
∵,、分别是、的中点,
∴,,
∴,
∵,
∴(三线合一).
24.1 圆的有关性质 同步检测
考试总分:100 分 考试时间:60 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 8 小题 ,每小题 3 分 ,共 24 分 )
?1.在半径为的中,弦长为的弦所对的圆心角为( )
A. B. C. D.
?2.下列说法不正确的是( )
A.圆是轴对称图形,它有无数条对称轴
B.圆的半径、弦长的一半、弦上的弦心距能组成一直角三角形,且圆的半径是此直角三角形的斜边
C.弦长相等,则弦所对的弦心距也相等
D.垂直于弦的直径平分这条弦,并且平分弦所对的弧
?3.已知的弦长为厘米,弦的弦心距为厘米,则的直径等于( )
A.厘米 B.厘米 C.厘米 D.厘米
?4.高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以为圆心的圆的一部分,路面米,净高米,则此圆的半径
A.米 B.米 C.米 D.米
?5.如图,为的直径,弦,垂足为点,连接,若,,则的长度为( )
A. B. C. D.
?6.如图,在中,若是的中点,则图中与相等的角有( )
A.个 B.个 C.个 D.个
?7.下列命题中,是真命题的为( )
A.三个点确定一个圆
B.一个圆中可以有无数条弦,但只有一条直径
C.圆既是轴对称图形,又是中心对称图形
D.同弧所对的圆周角与圆心角相等
?
8.如图,为的切线,切点为,点在上.如果,那么等于( )
A. B. C. D.
二、填空题(共 8 小题 ,每小题 3 分 ,共 24 分 )
?9.如图,的半径为,点在弦上,,,则的长是________.
?10.蔬菜基地圆弧形蔬菜大棚的剖面如图所示,已知,半径,则高度为________.
?11.“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何”此问题的实质就是解决下面的问题:“如图,为的直径,弦于点,,,求的长”.根据题意可得的长为________.
?12.如图所示,在中,点是的中点,,则为________度.
?13.已知,是直径,半径,点在上,且点与点在直径的两侧,连结,.若,则的度数是________.
?14.如图,为半的直径,为半圆弧的三等分点,过,两点的半的切线交于点,若的长是,则的长是________.
15.如图,海边立有两座灯塔、,暗礁分布在经过、两点的弓形(弓形的弧是的一部分)区域内,.为了避免触礁,轮船与、的张角的最大值为________.
?16.如图,弦垂直于的直径,垂足为,且,,则的长为________.
三、解答题(共 8 小题 ,每小题 9 分 ,共 72 分 )
?17.已知,画图说明满足下列条件的图形.
到点和的距离都等于的所有点组成的图形;
到点和的距离都小于的所有点组成的图形;
到点的距离大于,且到点的距离小于的所有点组成的图形.
?
18.如图,为的直径,弦于点,,,求直径的长.
?
19.已知:如图,、是的直径,,交于点,求证:.
?
20.如图,圆柱形水管内原有积水的水平面宽,水深.若水面上升,则此时水面宽为多少?
?
21.如图,、、都是的半径,
求证:
若平分,求的度数.
?
22.如图,已知是的直径,,分别是,的中点,,.求证:.
?
23.如图,、是半圆上的三等分点,直径,连接、,,垂足为,交于点.
求的度数;
求阴影部分的面积(结果保留和根号).
?
24.已知,如图,四边形中,,、分别是、的中点,则结论:
;
成立吗?请说明理由.
答案
1.B
2.C
3.C
4.B
5.A
6.C
7.C
8.C
9.
10.
11.
12.
13.或
14.
15.
16.
17.解:如图,分别以点和点为圆心,为半径画与,两圆的交点、为所求;
如图,分别以点和点为圆心,为半径画与,两圆的重叠部分为所求;如图,以点为圆心,为半径画,以点为圆心,为半径画,则中除去两圆的重叠部分为所求.
18.解:∵是的直径,
∴
∵
∴
设
∴
根据勾股定理:
解得
∴
19.证明:连接,
∵,
∴,,
∵,
∴,
∴.
20.解:如图所示,连接、.
设的半径是,则,.
∵,
∴.
在直角三角形中,根据勾股定理,得
,
解,得.
在直角三角形中,根据勾股定理,得
.
根据垂径定理,得.
21.证明:在中,
∵,,
∵.
∴.解:设.
∵平分,
∴,
∵,,
∴,
在中,
,
∴,
解得:,
∴.
22.证明:连结、,如图,
∵是的直径,,分别是,的中点,
∴,
∵,,
∴,
在和中,
,
∴,
∴,
∴.
23.解:连接,,
∵、是半圆上的三等分点,
∴,
∴,
∴,
∵,
∴,
∴;
由知,,
∵,,
∴是等边三角形,,
∵,
∴,
∴.
24.解:均成立.理由如下:
∵,、分别是、的中点,
∴,,
∴,
∵,
∴(三线合一).
同课章节目录
