2018年高中数学第2章圆锥曲线与方程2.2.1椭圆的标准方程课件3苏教版选修2_1(18张)
文档属性
| 名称 | 2018年高中数学第2章圆锥曲线与方程2.2.1椭圆的标准方程课件3苏教版选修2_1(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 800.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-27 00:00:00 | ||
图片预览






文档简介
课件18张PPT。问题1:你能举出生活中见到的椭圆吗?一、检查预习问题2:以上图形都给我们椭圆的印象,那在实际生产生活中该如何设计制造它的形状?从数学的角度上看,它们是不是严格意义上的椭圆? 二、质疑探究探究(一)实验操作
给你一根绳子、几个图钉、一只笔、一张纸如何画出一个椭圆?问题3:观察椭圆生成的动态过程,哪些量是不变的?哪些量是变化的?问题4:你能总结出椭圆是具备了什么特征的动点的轨
迹吗?平面内到两个定点F1,F2的距离的和等于常数 ( 大于F1F2 )的点的轨迹——椭圆两个定点F1,F2——椭圆的焦点两焦点间的距离——椭圆的焦距问题6:我们从图形的角度认识了椭圆,知道了确定椭圆的几何要素,那类比圆的研究过程,如果想进一步对椭圆进行研究,我们应该先做什么?问题7:回顾求曲线方程的基本步骤是什么?第一步:建系
第二步:设点
第三步:列式
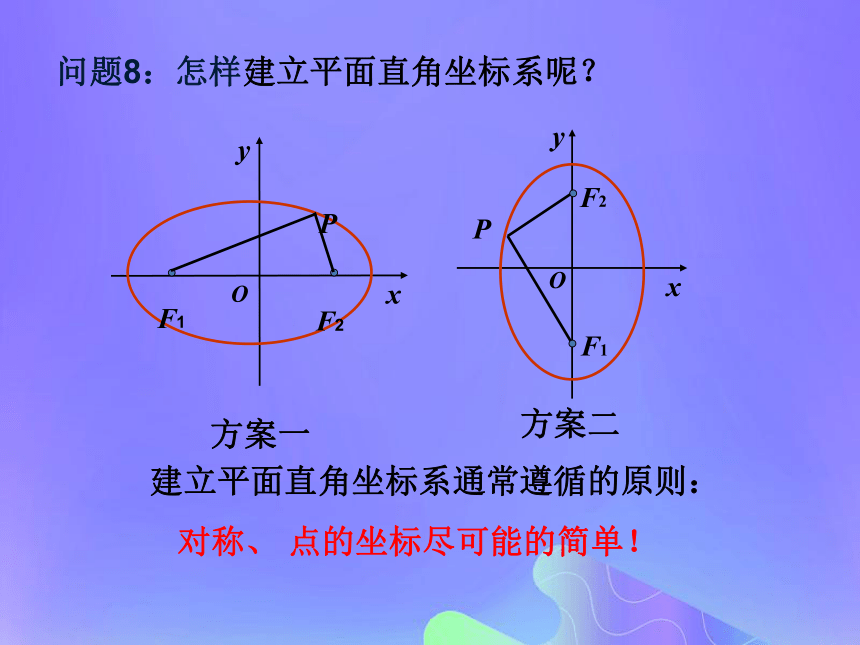
第四步:化简探究(二)椭圆的标准方程问题8:怎样建立平面直角坐标系呢?建立平面直角坐标系通常遵循的原则:
对称、 点的坐标尽可能的简单!方案一 以F1,F2所在直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系xOy,则F1,F2的坐标分别为(-c,0),(c,0).第一步:建系设椭圆上任意一点P的坐标为(x,y) ,第三步:列式根据椭圆定义知:PF1+PF2=2a,即: .第二步:设点第四步:化简 设椭圆的两个焦点分别为 F1,F2,
它们之间的距离为2c,椭圆上任意一点
P到F1,F2 的距离的和为2a(a>c).你有什么方法?第四步:化简两边再平方得:
a4-2a2cx+c2x2=a2x2-2a2cx+a2c2+a2y2,整理得:(a2-c2)x2+a2y2=a2(a2-c2).移项得: ,两边平方得:
,整理得: .第四步:化简因为a2(a2-c2) ≠0,所以两边同除以a2(a2-c2)得:
,又因为a2-c2>0,所以可设a2-c2=
b2(b>0),于是得:
.焦点在x轴上的椭圆的标准方程为O焦点在y轴上( )椭圆的标准方程F1(0 ,-c)、F2(0, c)F1(-c,0)、F2(c,0)如何根据标准方程判断焦点在哪个坐标轴上? 焦点在分母大的项所对应的坐标轴上. 已知一个运油车上的贮油罐横截面的外轮廓线
是一个椭圆,它的焦距为2.4m,外轮廓线上的点到两
个焦点距离的和为3m,若贮油罐车在一个加油站加油后,油面水平线距离油罐底部1.5米,问油面水平线的长度是多少米?数学应用O小结(1)两个焦点的坐标分别是(-2,0),(2,0)例2: 求适合下列条件的椭圆的标准方程.小结数学应用(2)a=5,c=3,焦点在x轴上;1、通过本节课的学习,你对椭圆的标准
方程有什么认识?
2、你有哪些收获?小结椭圆的标准方程定 义图
形方 程焦 点F(±c,0)F(0,±c) a,b,c
的关系PF1+PF2=2a,2a>F1F2(一)必做题1、P28 习题2.2(1) 1、2(二)选做题 已知F1,F2为椭圆 的焦点,过F1的直线交椭圆于A、B两点,若F2A+F2B=12,则AB长为多少?
作业
给你一根绳子、几个图钉、一只笔、一张纸如何画出一个椭圆?问题3:观察椭圆生成的动态过程,哪些量是不变的?哪些量是变化的?问题4:你能总结出椭圆是具备了什么特征的动点的轨
迹吗?平面内到两个定点F1,F2的距离的和等于常数 ( 大于F1F2 )的点的轨迹——椭圆两个定点F1,F2——椭圆的焦点两焦点间的距离——椭圆的焦距问题6:我们从图形的角度认识了椭圆,知道了确定椭圆的几何要素,那类比圆的研究过程,如果想进一步对椭圆进行研究,我们应该先做什么?问题7:回顾求曲线方程的基本步骤是什么?第一步:建系
第二步:设点
第三步:列式
第四步:化简探究(二)椭圆的标准方程问题8:怎样建立平面直角坐标系呢?建立平面直角坐标系通常遵循的原则:
对称、 点的坐标尽可能的简单!方案一 以F1,F2所在直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系xOy,则F1,F2的坐标分别为(-c,0),(c,0).第一步:建系设椭圆上任意一点P的坐标为(x,y) ,第三步:列式根据椭圆定义知:PF1+PF2=2a,即: .第二步:设点第四步:化简 设椭圆的两个焦点分别为 F1,F2,
它们之间的距离为2c,椭圆上任意一点
P到F1,F2 的距离的和为2a(a>c).你有什么方法?第四步:化简两边再平方得:
a4-2a2cx+c2x2=a2x2-2a2cx+a2c2+a2y2,整理得:(a2-c2)x2+a2y2=a2(a2-c2).移项得: ,两边平方得:
,整理得: .第四步:化简因为a2(a2-c2) ≠0,所以两边同除以a2(a2-c2)得:
,又因为a2-c2>0,所以可设a2-c2=
b2(b>0),于是得:
.焦点在x轴上的椭圆的标准方程为O焦点在y轴上( )椭圆的标准方程F1(0 ,-c)、F2(0, c)F1(-c,0)、F2(c,0)如何根据标准方程判断焦点在哪个坐标轴上? 焦点在分母大的项所对应的坐标轴上. 已知一个运油车上的贮油罐横截面的外轮廓线
是一个椭圆,它的焦距为2.4m,外轮廓线上的点到两
个焦点距离的和为3m,若贮油罐车在一个加油站加油后,油面水平线距离油罐底部1.5米,问油面水平线的长度是多少米?数学应用O小结(1)两个焦点的坐标分别是(-2,0),(2,0)例2: 求适合下列条件的椭圆的标准方程.小结数学应用(2)a=5,c=3,焦点在x轴上;1、通过本节课的学习,你对椭圆的标准
方程有什么认识?
2、你有哪些收获?小结椭圆的标准方程定 义图
形方 程焦 点F(±c,0)F(0,±c) a,b,c
的关系PF1+PF2=2a,2a>F1F2(一)必做题1、P28 习题2.2(1) 1、2(二)选做题 已知F1,F2为椭圆 的焦点,过F1的直线交椭圆于A、B两点,若F2A+F2B=12,则AB长为多少?
作业
