2018年高中数学第2章圆锥曲线与方程2.2.2椭圆的几何性质课件2苏教版选修2_1(15张)
文档属性
| 名称 | 2018年高中数学第2章圆锥曲线与方程2.2.2椭圆的几何性质课件2苏教版选修2_1(15张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-27 10:55:26 | ||
图片预览




文档简介
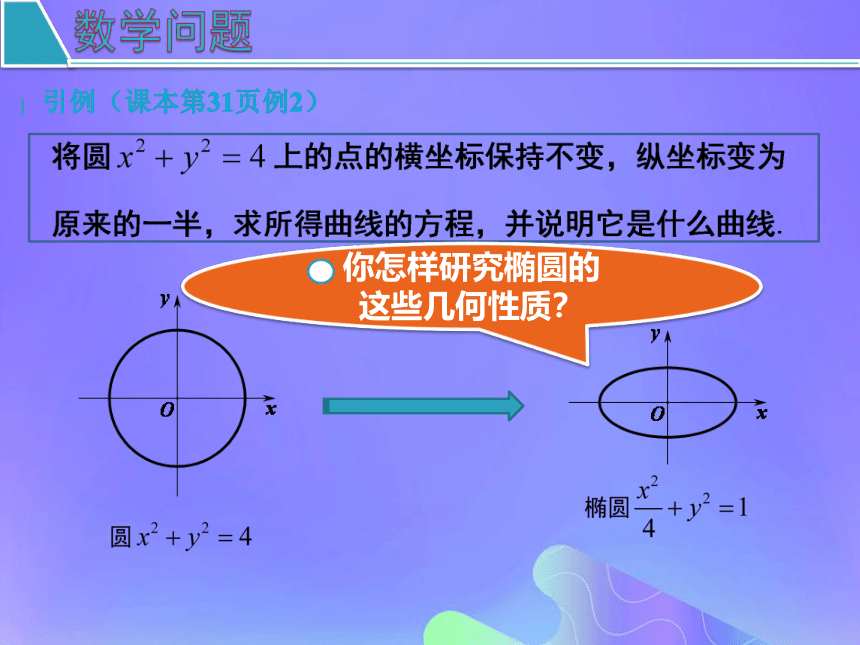
课件15张PPT。椭圆的几何性质课本第30页数学问题 汽车储油罐的横截面的外轮廓的形状像椭圆,把一个圆压扁了,也像椭圆.它们究竟是不是椭圆?
电影放映机上的聚光灯的反射镜、运用高能冲击波击碎肾结石的碎石机等仪器设备都是运用椭圆的性质制造的.怎样设计才能精确地制造它们?
借助于椭圆的方程,我们可以回答上述问题.那么,引例(课本第31页例2)
数学问题华罗庚(1910.11.12—1985.6.12)
世界著名数学家数缺形时少直观,
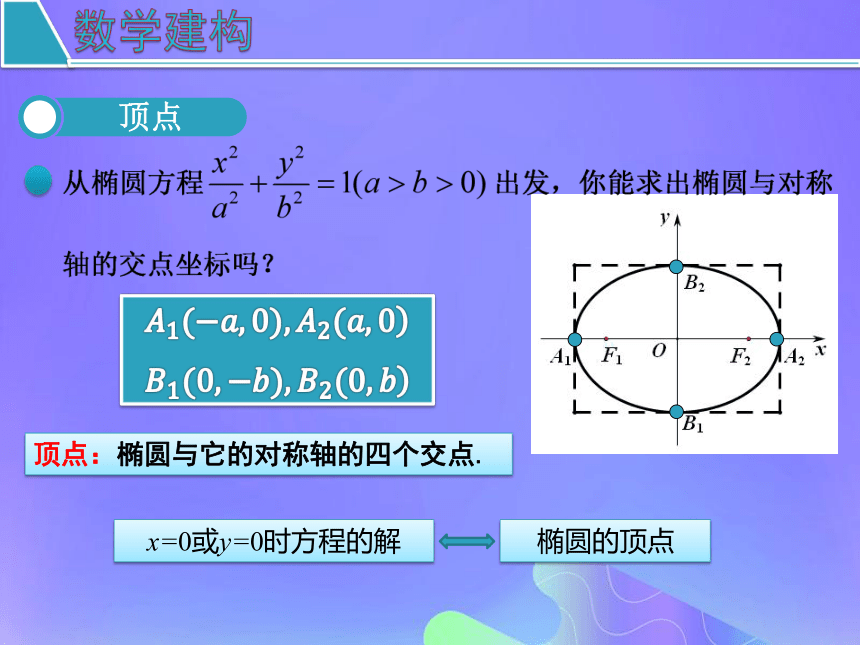
形缺数时难入微x=ax=-ay=by=-b数学建构坐标轴是椭圆的对称轴,
原点是椭圆的对称中心.椭圆的对称中心叫做椭圆的中心.数学建构yxo顶点:椭圆与它的对称轴的四个交点.数学建构长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴,它们的长分别等于2a和2b . a和b分别叫做椭圆的长半轴长和短半轴长.数学建构?数学运用 离心率跟天文学家有关,并且在天文学中广泛应用。
16世纪时天文学家发现太阳系的八大行星
都是绕着以太阳为焦点的椭圆形轨道运行,
这些轨道偏离太阳的程度称为“偏心率”,
其中在近日点处离太阳最近,偏离距离为a-c,
在远日点处离太阳最远,偏离距离为a+c,这两
个值不仅和运行轨道的扁平程度有关,还受轨道大小的影响,人们
需要构造一个“稳定”的量来表示偏心率,最后发现 的值和椭圆大小无关却能很好地刻画椭圆的扁平程度,因此,大家就选择了 表示离心率。数学文化数学运用
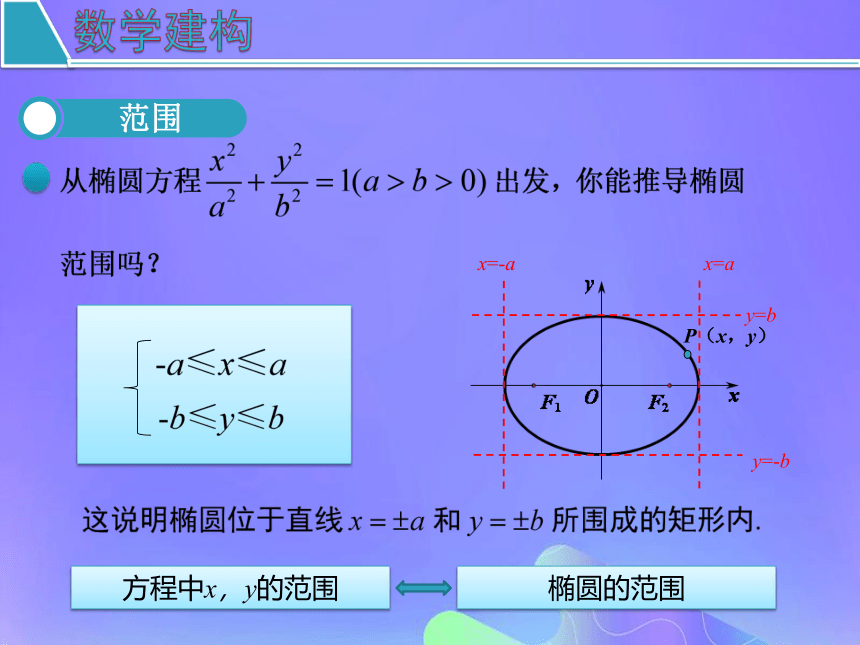
数学运用关于x轴、y轴对称,
关于原点对称-a≤x≤a,-b≤y≤b???知识回顾你能写出焦点在y轴的椭圆的几何性质吗?2.回顾我们的研究过程,我们是怎样研究椭圆的几何性质的? 1.本节课我们学习了什么知识?课堂小结以数解形课后作业
电影放映机上的聚光灯的反射镜、运用高能冲击波击碎肾结石的碎石机等仪器设备都是运用椭圆的性质制造的.怎样设计才能精确地制造它们?
借助于椭圆的方程,我们可以回答上述问题.那么,引例(课本第31页例2)
数学问题华罗庚(1910.11.12—1985.6.12)
世界著名数学家数缺形时少直观,
形缺数时难入微x=ax=-ay=by=-b数学建构坐标轴是椭圆的对称轴,
原点是椭圆的对称中心.椭圆的对称中心叫做椭圆的中心.数学建构yxo顶点:椭圆与它的对称轴的四个交点.数学建构长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴,它们的长分别等于2a和2b . a和b分别叫做椭圆的长半轴长和短半轴长.数学建构?数学运用 离心率跟天文学家有关,并且在天文学中广泛应用。
16世纪时天文学家发现太阳系的八大行星
都是绕着以太阳为焦点的椭圆形轨道运行,
这些轨道偏离太阳的程度称为“偏心率”,
其中在近日点处离太阳最近,偏离距离为a-c,
在远日点处离太阳最远,偏离距离为a+c,这两
个值不仅和运行轨道的扁平程度有关,还受轨道大小的影响,人们
需要构造一个“稳定”的量来表示偏心率,最后发现 的值和椭圆大小无关却能很好地刻画椭圆的扁平程度,因此,大家就选择了 表示离心率。数学文化数学运用
数学运用关于x轴、y轴对称,
关于原点对称-a≤x≤a,-b≤y≤b???知识回顾你能写出焦点在y轴的椭圆的几何性质吗?2.回顾我们的研究过程,我们是怎样研究椭圆的几何性质的? 1.本节课我们学习了什么知识?课堂小结以数解形课后作业
