2018年高中数学第3章空间向量与立体几何3.1.2共面向量定理课件2苏教版选修2_1(18张)
文档属性
| 名称 | 2018年高中数学第3章空间向量与立体几何3.1.2共面向量定理课件2苏教版选修2_1(18张) |  | |
| 格式 | zip | ||
| 文件大小 | 499.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-27 14:20:09 | ||
图片预览


文档简介
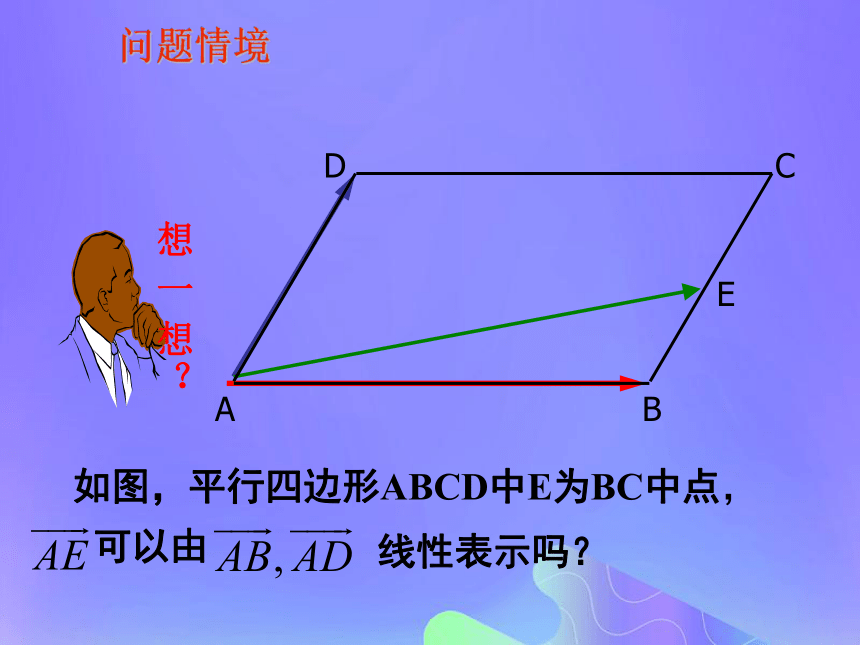
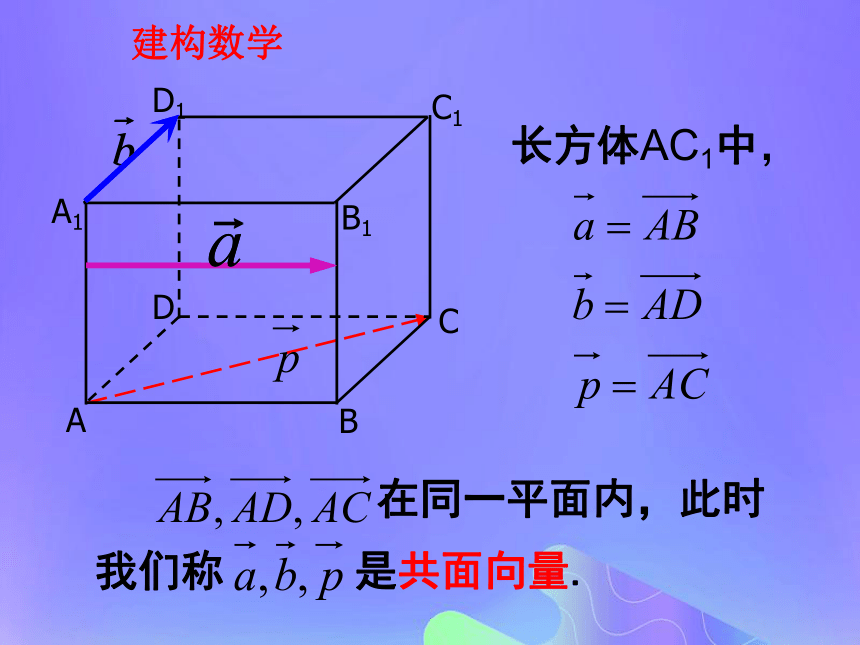
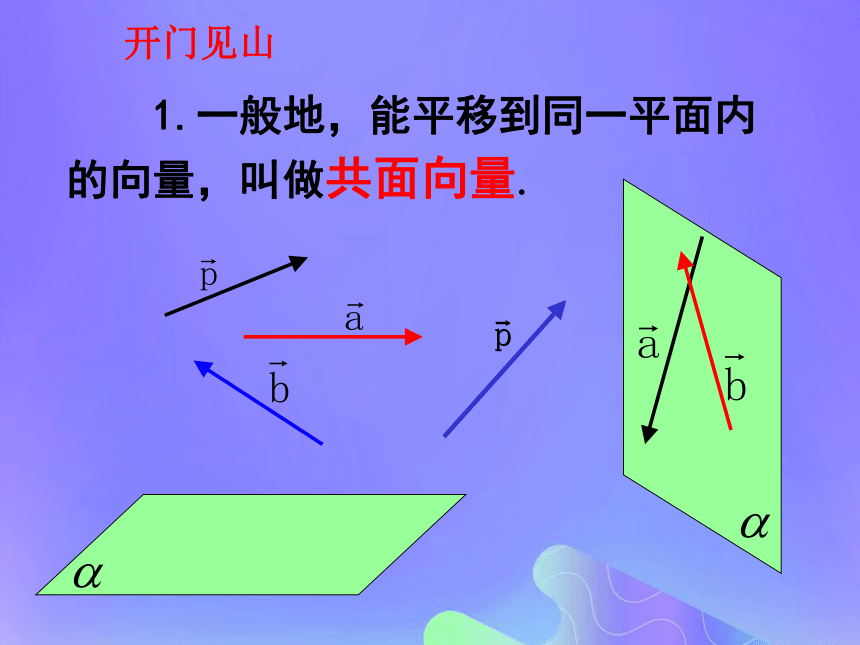
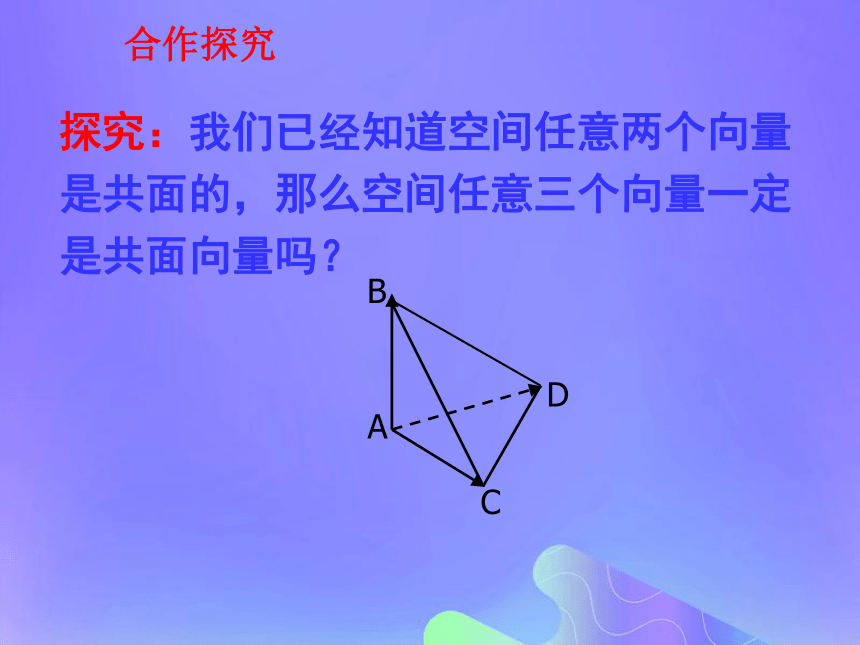
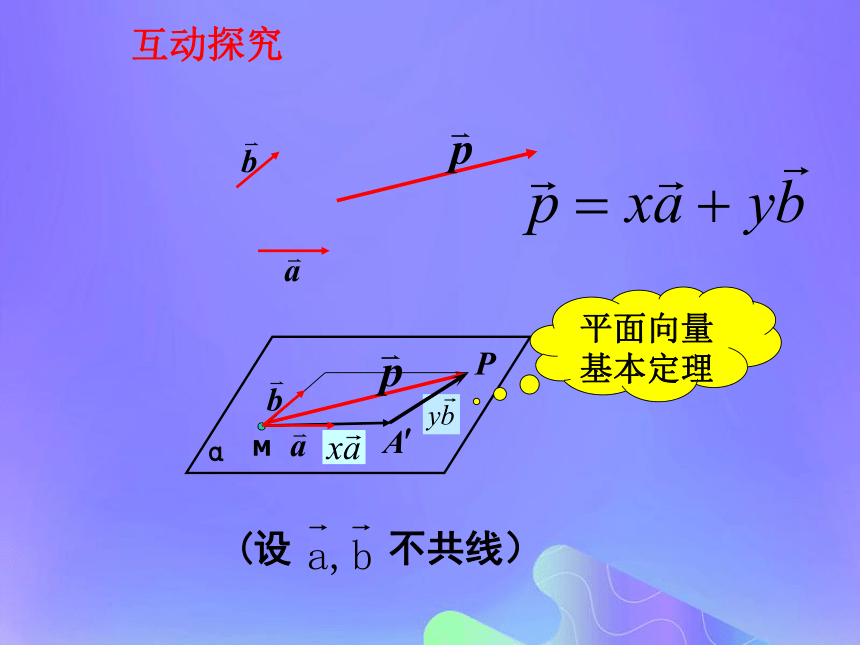
课件18张PPT。共面向量定理问题情境ACDBE如图,平行四边形ABCD中E为BC中点,可以由线性表示吗? 建构数学ABCDA1B1C1D1长方体AC1中, 1.一般地,能平移到同一平面内的向量,叫做共面向量.开门见山探究:我们已经知道空间任意两个向量是共面的,那么空间任意三个向量一定是共面向量吗?合作探究由此及彼平面向量基本定理互动探究2共面向量定理:平面向量的基本定理:共面向量定理:类比:
练习:判断正误
(1)在平面内共线的向量在空间不一定共线。
(2)空间的任意三个向量都共面。
(3)
(4)数学运用 (×)(×)(√)(×)例1.试问:P,A,B,C四点是否共面?登峰造极思考:
例2 如图,已知矩形ABCD和矩形ADEF所
在平面互相垂直,点M,N
分别在对角线BD,AE上,
且 求证:MN//平面CDE回味余香
1、知识点:
2、我们能用共面向量定理解决哪些常用
问题呢?
3、思想方法:
共面向量定理;类比方法的运用。大显身手课后作业
书P85-86 1,2,3,4,7,8,18Do It Youself!
Do It Now!—— 与同学们共勉曲径通幽
练习:判断正误
(1)在平面内共线的向量在空间不一定共线。
(2)空间的任意三个向量都共面。
(3)
(4)数学运用 (×)(×)(√)(×)例1.试问:P,A,B,C四点是否共面?登峰造极思考:
例2 如图,已知矩形ABCD和矩形ADEF所
在平面互相垂直,点M,N
分别在对角线BD,AE上,
且 求证:MN//平面CDE回味余香
1、知识点:
2、我们能用共面向量定理解决哪些常用
问题呢?
3、思想方法:
共面向量定理;类比方法的运用。大显身手课后作业
书P85-86 1,2,3,4,7,8,18Do It Youself!
Do It Now!—— 与同学们共勉曲径通幽
