2018年高中数学第3章空间向量与立体几何3.2.1直线的方向向量与平面的法向量课件2苏教版选修2_1(15张)
文档属性
| 名称 | 2018年高中数学第3章空间向量与立体几何3.2.1直线的方向向量与平面的法向量课件2苏教版选修2_1(15张) |  | |
| 格式 | zip | ||
| 文件大小 | 211.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-27 14:21:55 | ||
图片预览




文档简介
课件15张PPT。3.2.1直线的方向向量与平面的法向量学生活动1:每人拿出一本书和一支笔,从笔与书本平行开始转动笔,你发现了什么?
再让笔不动,转动书本,你又发现了什么?学生活动2:每人拿出两本书,从两本书平行开始转动其中的一本书,你发现了什么?
学生活动在平面内我们可以用直线的倾斜角或斜率刻画直线的方向,在平面向量中也提到了直线的方向向量,在空间怎样用向量来表示直线的方向?答:我们把这样的向量称之为直线的方向向量。直线的方向向量的定义:思考:已知一条直线a,如何快速地确定直线a的一个方向向量?问题情景1:我们怎样用向量来刻画平面的“方向”呢?这样的向量跟平面有
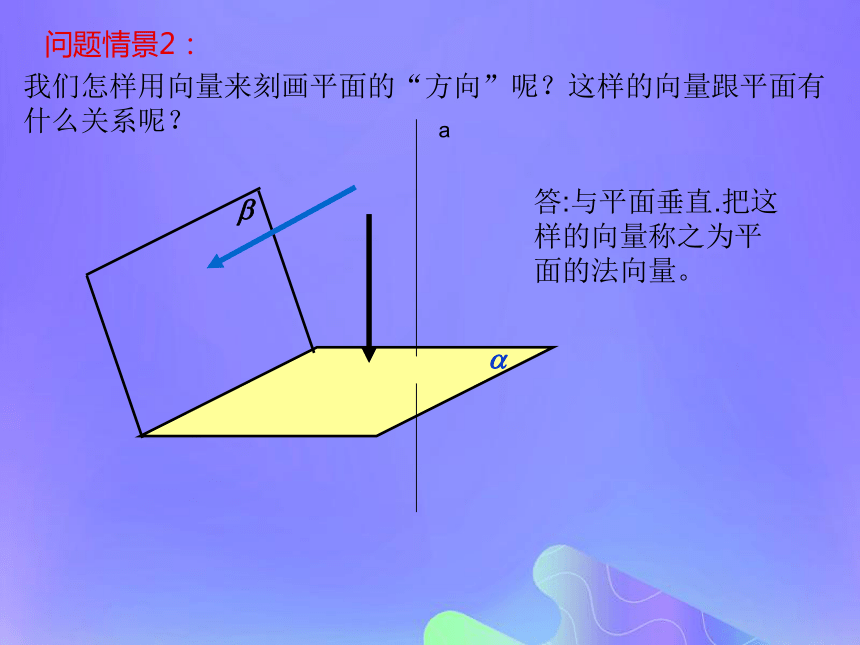
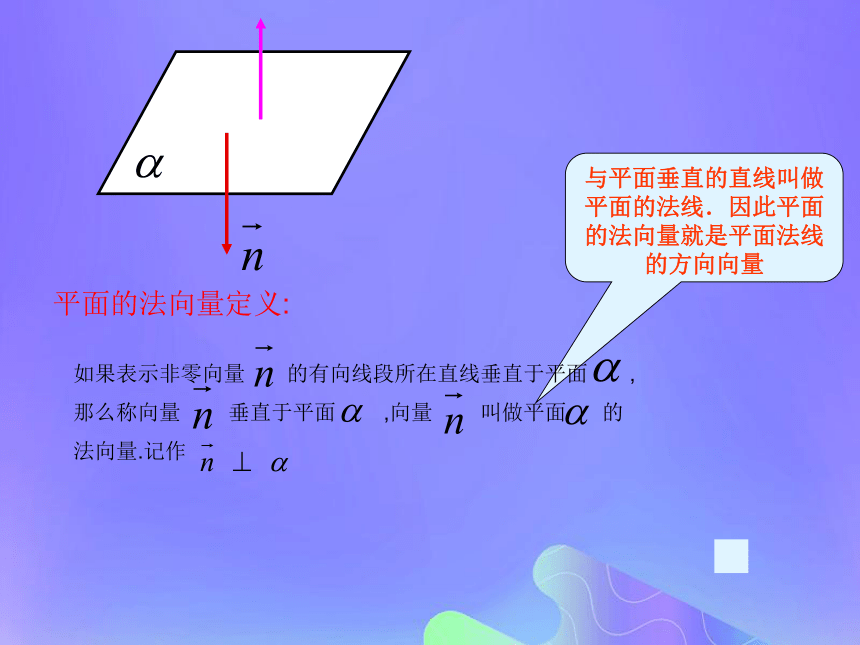
什么关系呢?答:与平面垂直.把这样的向量称之为平面的法向量。问题情景2:平面的法向量定义:与平面垂直的直线叫做平面的法线.因此平面的法向量就是平面法线的方向向量几点注意:
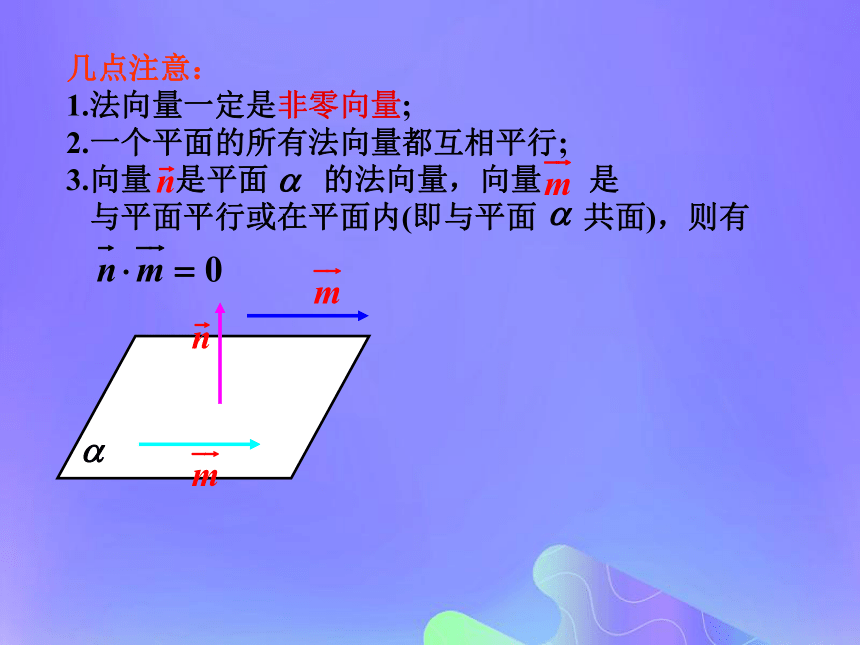
1.法向量一定是非零向量;
2.一个平面的所有法向量都互相平行;
3.向量 是平面 的法向量,向量 是
与平面平行或在平面内(即与平面 共面),则有则各点的坐标为A(1,0,0),C(0,1,0),D1(0,0,1),B1(1,1,1)。变题求平面ACD1的一个法向量待定系数法求平面的法向量巩固练习思考与交流课堂小结:一、直线的方向向量定义:二、平面的法向量定义 (1)可设法向量的坐标
(2)用它与平面内两条不共线向量分别求数量积结果为0;
(3)解方程组求得一组解即可。
三、求法:课后思考(1)已知平面的法向量,这个平面是否唯一确定?
(2)已知平面内一点和平面的法向量,这个平面是否唯一确定?
谢谢各位!
再让笔不动,转动书本,你又发现了什么?学生活动2:每人拿出两本书,从两本书平行开始转动其中的一本书,你发现了什么?
学生活动在平面内我们可以用直线的倾斜角或斜率刻画直线的方向,在平面向量中也提到了直线的方向向量,在空间怎样用向量来表示直线的方向?答:我们把这样的向量称之为直线的方向向量。直线的方向向量的定义:思考:已知一条直线a,如何快速地确定直线a的一个方向向量?问题情景1:我们怎样用向量来刻画平面的“方向”呢?这样的向量跟平面有
什么关系呢?答:与平面垂直.把这样的向量称之为平面的法向量。问题情景2:平面的法向量定义:与平面垂直的直线叫做平面的法线.因此平面的法向量就是平面法线的方向向量几点注意:
1.法向量一定是非零向量;
2.一个平面的所有法向量都互相平行;
3.向量 是平面 的法向量,向量 是
与平面平行或在平面内(即与平面 共面),则有则各点的坐标为A(1,0,0),C(0,1,0),D1(0,0,1),B1(1,1,1)。变题求平面ACD1的一个法向量待定系数法求平面的法向量巩固练习思考与交流课堂小结:一、直线的方向向量定义:二、平面的法向量定义 (1)可设法向量的坐标
(2)用它与平面内两条不共线向量分别求数量积结果为0;
(3)解方程组求得一组解即可。
三、求法:课后思考(1)已知平面的法向量,这个平面是否唯一确定?
(2)已知平面内一点和平面的法向量,这个平面是否唯一确定?
谢谢各位!
