2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.2.1双曲线及其标准方程课件(24张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.2.1双曲线及其标准方程课件(24张) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-27 14:38:24 | ||
图片预览








文档简介
课件24张PPT。2.2.1双曲线及其标准方程学习目标知识目标:
理解并掌握双曲线的定义;
掌握双曲线的标准方程及其求法.
能力目标:
通过“实验观察”、“思考探究”与合作交流等一系列数学活动,培养学生观察、类比、分析、概括的能力以及逻辑思维的能力,体会数学思想方法在解题中的应用。
情感目标:
通过实例的引入和剖析让学生再一次感受到数学来源于
实践又反作用于实践,生活中处处有数学,体会数学之
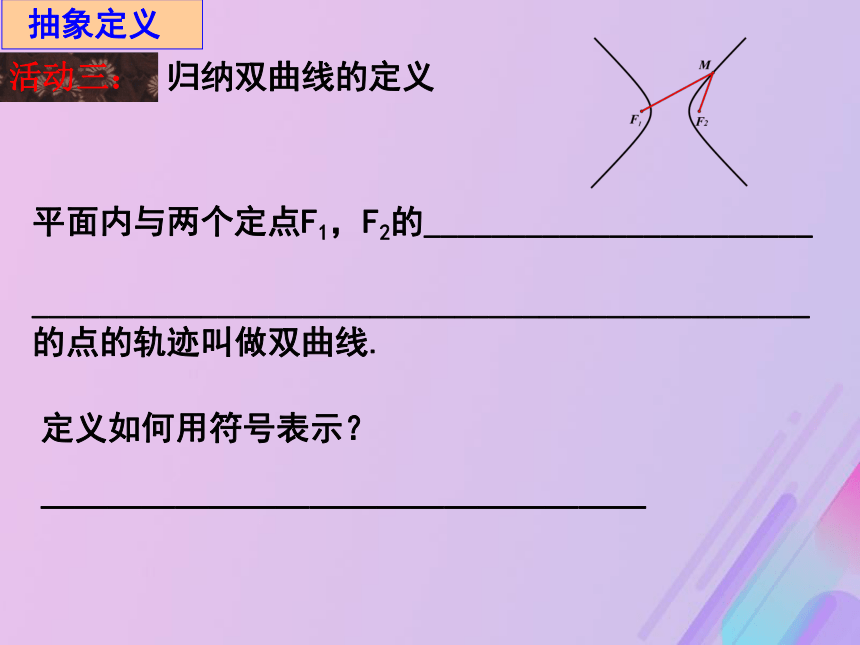
美。1、椭圆是如何定义的?3、椭圆标准方程中字母a、b、c的关系如何?2、椭圆的标准方程是什么?如何判断焦点所在的轴?复习旧知,做好铺垫焦点在分母大的轴上设置情景,引发探究探究1、概念引入(选修1-1 习题2.1第7题)活动一:思考:在本题中点Q与点O、点A满足怎样的几何关系?点Q的轨迹如何? 动画展示,再次感受活动二:探究2、概念引入(选修1-1 习题2.2第5题)思考:在本题中点Q与点O、点A满足怎样的几何关系?点Q的轨迹如何?要求:组长调控,组织讨论,做好展示点评准备. 动画展示,直观感知平面内与两个定点F1,F2的_______________________
______________________________________________的点的轨迹叫做双曲线. 抽象定义活动三:归纳双曲线的定义定义如何用符号表示?
—————————————————— 讨论2a与2c的大小关系对轨迹的影响(1)0<2a<2c:动点M的轨迹是什么?(2)2a=2c:动点M的轨迹又是什么?(3)2a>2c:动点M的轨迹又是什么?动点M的轨迹是双曲线;深入挖掘活动四:感受生活中的双曲线拉链实验类比迁移,推导方程问题探究:
1、求动点的轨迹方程分哪几步?
2、如何建立坐标系能使求出的双曲线方程简单?
3、设出点坐标,用坐标表示出动点M满足的几何关系.
4、类比椭圆标准方程的的化简过程思考所列式子如何化简.别想一下到达顶峰,必须先由脚踏实地开始!活动五:双曲线的标准方程的推导以 F1F2 所在的直线为x轴,线段F1F2的垂直平分线为y轴。(如图)设M(x,y)是双曲线上的任意一点,则F1,F2的坐标分别为(-c,0),(c,0)由定义可知:双曲线就是点M适合下列条件的集合:P={M| ||MF1|-|MF2||=2a}两边平方整理得:(c2-a2)x2-a2y2=a2(c2-a2)由定义,2c>2a,即c>a,所以c2-a2>0设c2-a2=b2(b>0)代入得b2x2-a2y2=a2b2两边同除以a2b2得:两边平方得:(对换x,y可得)焦点在y轴上焦点在x轴上记忆:正项定焦轴双曲线的标准方程练习反馈,巩固提高例1、判断下列方程是否表示双曲线.若是说出焦点所在轴并求出焦点坐标.例2:已知两定点F1(-5,0),F2(5,0),若点P满足
,求点P的轨迹方程.变式训练1:2、求适合下列条件的双曲线方程.(1) = 4,b=5,焦点在y轴上.(3) = 3,c=5.当堂检测1、判断下列方程是否表示双曲线.若是求出焦点坐标.(2)与双曲线 的焦点相同,b=3.提炼总结,反思提高你今天收获了什么?知识内容:
思想方法:
情感态度价值观:
| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)F ( ±c, 0) F(0,±c)知识内容:思想方法:
数形结合思想;化归与转化思想;分类与整合思想;
类比思想;由特殊到一般思想.情感态度价值观:
从双曲线定义的发现、双曲线的应用,树立了数学知识源于生活,应用于生活的意识,学以致用,树立正确的人生观,价值观。作业必做题:1、课本48页练习1、2
2、归纳总结椭圆与双曲线的联系与区别
思考与探究题:
提高作业:类比椭圆中 所构成的直角三角形找出双曲线中 所构成的直角三角形。
理解并掌握双曲线的定义;
掌握双曲线的标准方程及其求法.
能力目标:
通过“实验观察”、“思考探究”与合作交流等一系列数学活动,培养学生观察、类比、分析、概括的能力以及逻辑思维的能力,体会数学思想方法在解题中的应用。
情感目标:
通过实例的引入和剖析让学生再一次感受到数学来源于
实践又反作用于实践,生活中处处有数学,体会数学之
美。1、椭圆是如何定义的?3、椭圆标准方程中字母a、b、c的关系如何?2、椭圆的标准方程是什么?如何判断焦点所在的轴?复习旧知,做好铺垫焦点在分母大的轴上设置情景,引发探究探究1、概念引入(选修1-1 习题2.1第7题)活动一:思考:在本题中点Q与点O、点A满足怎样的几何关系?点Q的轨迹如何? 动画展示,再次感受活动二:探究2、概念引入(选修1-1 习题2.2第5题)思考:在本题中点Q与点O、点A满足怎样的几何关系?点Q的轨迹如何?要求:组长调控,组织讨论,做好展示点评准备. 动画展示,直观感知平面内与两个定点F1,F2的_______________________
______________________________________________的点的轨迹叫做双曲线. 抽象定义活动三:归纳双曲线的定义定义如何用符号表示?
—————————————————— 讨论2a与2c的大小关系对轨迹的影响(1)0<2a<2c:动点M的轨迹是什么?(2)2a=2c:动点M的轨迹又是什么?(3)2a>2c:动点M的轨迹又是什么?动点M的轨迹是双曲线;深入挖掘活动四:感受生活中的双曲线拉链实验类比迁移,推导方程问题探究:
1、求动点的轨迹方程分哪几步?
2、如何建立坐标系能使求出的双曲线方程简单?
3、设出点坐标,用坐标表示出动点M满足的几何关系.
4、类比椭圆标准方程的的化简过程思考所列式子如何化简.别想一下到达顶峰,必须先由脚踏实地开始!活动五:双曲线的标准方程的推导以 F1F2 所在的直线为x轴,线段F1F2的垂直平分线为y轴。(如图)设M(x,y)是双曲线上的任意一点,则F1,F2的坐标分别为(-c,0),(c,0)由定义可知:双曲线就是点M适合下列条件的集合:P={M| ||MF1|-|MF2||=2a}两边平方整理得:(c2-a2)x2-a2y2=a2(c2-a2)由定义,2c>2a,即c>a,所以c2-a2>0设c2-a2=b2(b>0)代入得b2x2-a2y2=a2b2两边同除以a2b2得:两边平方得:(对换x,y可得)焦点在y轴上焦点在x轴上记忆:正项定焦轴双曲线的标准方程练习反馈,巩固提高例1、判断下列方程是否表示双曲线.若是说出焦点所在轴并求出焦点坐标.例2:已知两定点F1(-5,0),F2(5,0),若点P满足
,求点P的轨迹方程.变式训练1:2、求适合下列条件的双曲线方程.(1) = 4,b=5,焦点在y轴上.(3) = 3,c=5.当堂检测1、判断下列方程是否表示双曲线.若是求出焦点坐标.(2)与双曲线 的焦点相同,b=3.提炼总结,反思提高你今天收获了什么?知识内容:
思想方法:
情感态度价值观:
| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)F ( ±c, 0) F(0,±c)知识内容:思想方法:
数形结合思想;化归与转化思想;分类与整合思想;
类比思想;由特殊到一般思想.情感态度价值观:
从双曲线定义的发现、双曲线的应用,树立了数学知识源于生活,应用于生活的意识,学以致用,树立正确的人生观,价值观。作业必做题:1、课本48页练习1、2
2、归纳总结椭圆与双曲线的联系与区别
思考与探究题:
提高作业:类比椭圆中 所构成的直角三角形找出双曲线中 所构成的直角三角形。
