2018年高中数学第二章圆锥曲线与方程2.2.2椭圆的几何性质课件7新人教B版选修2_1(19张)
文档属性
| 名称 | 2018年高中数学第二章圆锥曲线与方程2.2.2椭圆的几何性质课件7新人教B版选修2_1(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 884.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-27 00:00:00 | ||
图片预览






文档简介
课件19张PPT。椭圆的几何性质1.椭圆的定义:平面内与两个定点F1、F2的距离的和等于常数
(大于|F1F2 |)的点的轨迹(或集合)叫做椭圆。2.椭圆的标准方程是:3.椭圆中a,b,c的关系是:a2=b2+c2(焦点在x轴上的椭圆标准方程)(焦点在y轴上的椭圆标准方程)小组探究问题1:能否用方程说明椭圆上点的横、纵坐标的范围?
问题2:能否用代数法说明椭圆具有什么样的对称性?
问题3:椭圆上的顶点如何定义?
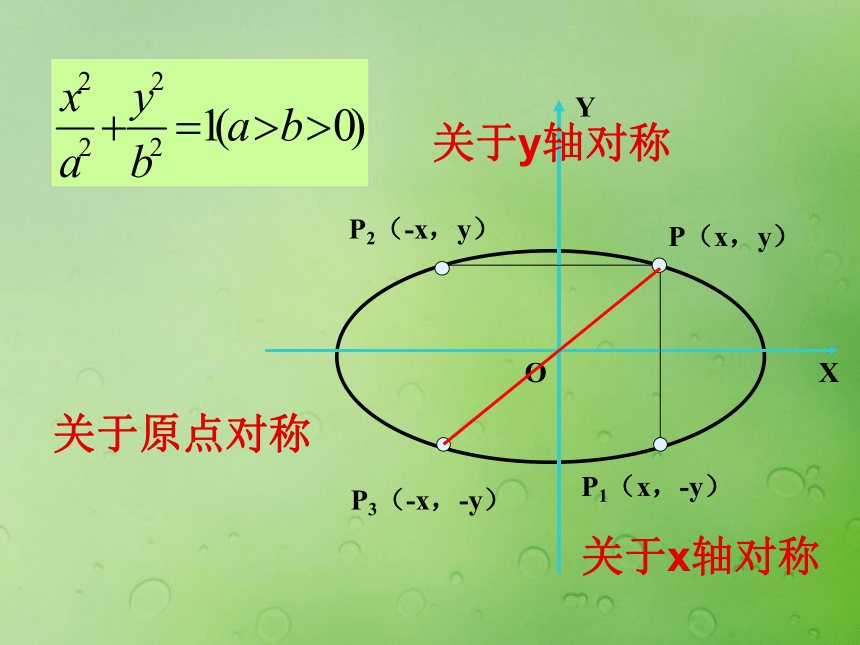
问题4:怎样刻画椭圆的扁圆程度?一、椭圆的范围即由和由-a≤x≤a , -b≤y≤b5(1)把x换成-x,方程不变,图象关于y轴对称;(2)把y换成-y,方程不变,图象关于x轴对称;(3)把x换成-x,同时把y换成-y方程不变,图象 关于原点成中心对称。二、椭圆的对称性关于x轴对称关于y轴对称关于原点对称7三、椭圆的顶点
*顶点:椭圆与它的对称轴共有四个交点,即A1,A2,B1,B2,这四个点叫做椭圆的顶点。
*长轴、短轴:线段A1A2叫做椭圆的长轴,它的长等于2a;线段B1B2叫做椭圆的短轴,它的长等于2b;a、b分别叫做椭圆的长半轴长和短半轴长。令 x=0,得 y=?说明椭圆与 y轴的交点?令 y=0,得 x=?说明椭圆与 x轴的交点?a2=b2+c2四、椭圆的离心率[1]离心率的取值范围:[2]离心率对椭圆形状的影响:
1)e 越接近 1,c 就越接近 a,请问:此时椭圆的变化情况?
b就越小,此时椭圆就越扁。 2)e 越接近 0,c 就越接近 0,请问:此时椭圆又是如何变化的?b就越大,此时椭圆就越趋近于圆。3) 如果a=b,则c=0,两个焦点重合,椭圆的标准方程就变为圆的方程:离心率:因为 a > c > 0,所以0小组互动展示你的风采!
【例1】、椭圆方程为4x2+9y2=36的长轴长是____、短轴长是____、焦距是:____、离心率是______、焦点坐标是_____ 、顶点坐标是_________。 课堂典例考点一:根据椭圆的标准方程研究其几何性质回顾总结本节课你有什么收获?一框两轴七点,e来刻画圆和扁 分别关于x轴和y轴轴对称;关于原点中心对称课后作业p46 练习A 1、2、3
课后探究:教材例2
题中说明卫星运行的近地点、远地点及
轨道的焦点在同一条直线上。所有卫星的近
地点、远地点、焦点都是这样吗?为什么?
利用标准方程探究椭圆上点到焦点的距离最
大和最小的点。谢谢!
(大于|F1F2 |)的点的轨迹(或集合)叫做椭圆。2.椭圆的标准方程是:3.椭圆中a,b,c的关系是:a2=b2+c2(焦点在x轴上的椭圆标准方程)(焦点在y轴上的椭圆标准方程)小组探究问题1:能否用方程说明椭圆上点的横、纵坐标的范围?
问题2:能否用代数法说明椭圆具有什么样的对称性?
问题3:椭圆上的顶点如何定义?
问题4:怎样刻画椭圆的扁圆程度?一、椭圆的范围即由和由-a≤x≤a , -b≤y≤b5(1)把x换成-x,方程不变,图象关于y轴对称;(2)把y换成-y,方程不变,图象关于x轴对称;(3)把x换成-x,同时把y换成-y方程不变,图象 关于原点成中心对称。二、椭圆的对称性关于x轴对称关于y轴对称关于原点对称7三、椭圆的顶点
*顶点:椭圆与它的对称轴共有四个交点,即A1,A2,B1,B2,这四个点叫做椭圆的顶点。
*长轴、短轴:线段A1A2叫做椭圆的长轴,它的长等于2a;线段B1B2叫做椭圆的短轴,它的长等于2b;a、b分别叫做椭圆的长半轴长和短半轴长。令 x=0,得 y=?说明椭圆与 y轴的交点?令 y=0,得 x=?说明椭圆与 x轴的交点?a2=b2+c2四、椭圆的离心率[1]离心率的取值范围:[2]离心率对椭圆形状的影响:
1)e 越接近 1,c 就越接近 a,请问:此时椭圆的变化情况?
b就越小,此时椭圆就越扁。 2)e 越接近 0,c 就越接近 0,请问:此时椭圆又是如何变化的?b就越大,此时椭圆就越趋近于圆。3) 如果a=b,则c=0,两个焦点重合,椭圆的标准方程就变为圆的方程:离心率:因为 a > c > 0,所以0
【例1】、椭圆方程为4x2+9y2=36的长轴长是____、短轴长是____、焦距是:____、离心率是______、焦点坐标是_____ 、顶点坐标是_________。 课堂典例考点一:根据椭圆的标准方程研究其几何性质回顾总结本节课你有什么收获?一框两轴七点,e来刻画圆和扁 分别关于x轴和y轴轴对称;关于原点中心对称课后作业p46 练习A 1、2、3
课后探究:教材例2
题中说明卫星运行的近地点、远地点及
轨道的焦点在同一条直线上。所有卫星的近
地点、远地点、焦点都是这样吗?为什么?
利用标准方程探究椭圆上点到焦点的距离最
大和最小的点。谢谢!
